- Research
- Open access
- Published:
On products of multivalent close-to-star functions
Journal of Inequalities and Applications volume 2015, Article number: 5 (2015)
Abstract
In the present paper we define a class of products of multivalent close-to-starfunctions and determine the set of pairs  ,
,  , such that every function from the class maps thedisk
, such that every function from the class maps thedisk  onto a domain starlike with respect to theorigin. Some consequences of the obtained result are also considered.
onto a domain starlike with respect to theorigin. Some consequences of the obtained result are also considered.
MSC: 30C45, 30C50, 30C55.
1 Introduction
Let  denotethe class of functions which are analytic in
denotethe class of functions which are analytic in  , where
, where

and let  denote the class of functions
denote the class of functions  of the form
of the form

A function  is said to be starlike of orderα in
is said to be starlike of orderα in  if
if

A function  is said to be convex of orderα in
is said to be convex of orderα in  if
if

We denote by  the class of all functions
the class of all functions  , which are convex of order α in
, which are convex of order α in and by
and by  we denote the class of all functions
we denote the class of all functions , which are starlike of order α in
, which are starlike of order α in .We also set
.We also set  .
.
Let ℋ be a subclass of the class  . We define the radius of starlikeness of theclass ℋ by
. We define the radius of starlikeness of theclass ℋ by

We denote by  ,
,  , the class of functions
, the class of functions  such that
such that  and
and

where Argw denote the principal argument of the complex number w(i.e. from the interval  ). The class
). The class  is the well-known class of Carathéodoryfunctions.
is the well-known class of Carathéodoryfunctions.
We say that a function  belongs to the class
belongs to the class  if there exists a function
if there exists a function  such that
such that

In particular, we denote

The class  is the well-known class of close-to-star functionswith argument 0.
is the well-known class of close-to-star functionswith argument 0.
Silverman [1] introduced the class of functions F given by the formula

where  ,
,  (
( ) are positive real numbers satisfying the followingconditions:
) are positive real numbers satisfying the followingconditions:

Dimkov [2] studied the class of functions F given by the formula

where  (
( ) are complex numbers satisfying the condition
) are complex numbers satisfying the condition

Let p, n be positive integer and let a, m,M, N be positive real numbers,  . Moreover, let
. Moreover, let

be fixed vectors, with

We denote by  the class of functions F given by theformula
the class of functions F given by theformula

By  we denote union of all classes
we denote union of all classes for which
for which

Finally, let us denote

It is clear that the class  contains functions F given by the formula(2) for which
contains functions F given by the formula(2) for which

Aleksandrov [3] stated and solved the following problem.
Problem 1 Let ℋ be the class of functions  that are univalent in
that are univalent in  and let
and let be a domain starlike with respect to an inner pointω with smooth boundary given by the formula
be a domain starlike with respect to an inner pointω with smooth boundary given by the formula

Find conditions for the function  such that for each
such that for each  the image domain
the image domain  is starlike with respect to
is starlike with respect to  .
.
Świtoniak and Stankiewicz [4, 5], Dimkov and Dziok [6] (see also [7]) have investigated a similar problem of generalized starlikeness.
Problem 2 Let  . Determine the set
. Determine the set  of all pairs
of all pairs  , such that
, such that

and every function  maps the disk
maps the disk  onto a domain starlike with respect to the origin.The set
onto a domain starlike with respect to the origin.The set  is called the set of generalized starlikeness of theclass ℋ.
is called the set of generalized starlikeness of theclass ℋ.
We note that

In this paper we determine the sets  ,
,  and
and  . The sets of generalized starlikeness for somesubclasses of the defined classes are also considered. Moreover, we obtain the radiiof starlikeness of these classes of functions.
. The sets of generalized starlikeness for somesubclasses of the defined classes are also considered. Moreover, we obtain the radiiof starlikeness of these classes of functions.
2 Main results
We start from listing some lemmas which will be useful later on.
Lemma 1[5]
A function maps the disk
maps the disk ,
,  , onto a domain starlike with respect to theorigin if and only if
, onto a domain starlike with respect to theorigin if and only if

For a function  it is easy to verify that
it is easy to verify that

Thus, after some calculations we get the following lemma.
Lemma 2Let ,
,  ,
,  . Then
. Then

Lemma 3[8]
If , then
, then

Theorem 1Letm, b, cbe defined by (3) and set


where




Moreover, set

If , then a function
, then a function maps the disk
maps the disk onto a domain starlike with respect to the origin. The result is sharpfor
onto a domain starlike with respect to the origin. The result is sharpfor and for
and for the set ℬ cannot be larger than
the set ℬ cannot be larger than . It means that
. It means that


Proof Let F belong to the class  and let
and let  satisfy (5). The functions
satisfy (5). The functions

belong to the class  together with the functions
together with the functions  . Thus, by (2) the functions
. Thus, by (2) the functions

belong to the class  together with the function
together with the function  . In consequence, we have
. In consequence, we have

Therefore, without loss of generality we may assume that a is nonnegativereal number. Since  , there exist functions
, there exist functions  and
and  such that
such that

or equivalently

After logarithmic differentiation of the equality (2) we obtain

Thus, using (18) we have

By Lemma 2 and Lemma 3 we obtain

Setting  and using (3) the above inequality yields
and using (3) the above inequality yields

By Lemma 1 it is sufficient to show that the right-hand side of the lastinequality is nonnegative, that is,

If we put

then we obtain

Thus, using the equality

we obtain

The discriminant Δ of  is given by
is given by

where


Let

First, we discuss the case  . Thus, the inequality (21) is satisfied for every
. Thus, the inequality (21) is satisfied for every if one of the following conditions is fulfilled:
if one of the following conditions is fulfilled:
1∘ ,
,
2∘ ,
,  and
and  ,
,
3∘ ,
,  and
and  ,
,
where

Ad 1∘. Since  , by (22), the condition
, by (22), the condition  is equivalent to the inequality
is equivalent to the inequality . Then
. Then

where φ is defined by (13). Let

Then γ is the curve which is tangent to the straight lines and
and  at the points
at the points

where  ,
,  , q are defined by (10), (11), (12),respectively.
, q are defined by (10), (11), (12),respectively.
Moreover, γ cuts the straight line  at the points
at the points

Since

we have

and consequently

where φ is defined by (13) (see Figure 1).
Ad 2∘. Let

It is easy to verify that

where q is defined by (12) and

Since

we see that

Thus, the inequality  is true if
is true if  . The inequality
. The inequality  may be written in the form
may be written in the form

The hyperbola  , which is the boundary of the set of all pairs
, which is the boundary of the set of all pairs satisfying (31), cuts the boundary of the setD at the point
satisfying (31), cuts the boundary of the setD at the point  defined by (27) and at the point
defined by (27) and at the point , where
, where

It is easy to verify that

Thus we determine the set

where φ is defined by (13) (see Figure 2).
Ad 3∘. Let

and let q and  be defined by (12) and (29), respectively. Then
be defined by (12) and (29), respectively. Then

Moreover, by (30) we have

Thus, we conclude that the inequality  is true if
is true if  . The inequality
. The inequality  may be written in the form
may be written in the form

The hyperbola  , which is the boundary of the set of all pairs
, which is the boundary of the set of all pairs satisfying (34), cuts the boundary of the setD at the point
satisfying (34), cuts the boundary of the setD at the point  defined by (27) and at the point
defined by (27) and at the point , where
, where  is defined by (32). Thus, we describe the set
is defined by (32). Thus, we describe the set

where φ is defined by (13) (see Figure 2).The union of the sets  ,
,  ,
,  defined by (28), (33), and (35) gives the set
defined by (28), (33), and (35) gives the set

Thus, by (17) we have

where  is defined by (8).
is defined by (8).
Now, let  . Then the inequality (21) is satisfied for every
. Then the inequality (21) is satisfied for every if
if

We see that

where q and  are defined by (12) and (29), respectively. Since
are defined by (12) and (29), respectively. Since

the condition (37) is satisfied if  and
and

Let  . Then by (21) we obtain
. Then by (21) we obtain

The above inequality holds for every  if
if  and
and

or equivalently (38). Thus, by (17) we have

where  is defined by (9). Because the function
is defined by (9). Because the function

belongs to the class  , and for
, and for  ,
,  ,
,  we have
we have

Lemma 1 yields

From (36) and (41) we have (15), while (39) and (41) give (16), which completes theproof. □
Since the set ℬ defined by (14) is dependent only of m, b,c, the following result is an immediate consequence ofTheorem 1.
Theorem 2Let ℬ be defined by (14). If , then a function
, then a function maps the disk
maps the disk onto a domain starlike with respect to the origin. The obtained resultis sharp for
onto a domain starlike with respect to the origin. The obtained resultis sharp for and for
and for the set ℬ cannot be larger than
the set ℬ cannot be larger than , where
, where is defined by (8). It means that
is defined by (8). It means that

The functions described by (40), with (3) are the extremalfunctions.
Theorem 3

where

The equality in (42) is realized by the functionFof the form

Proof Let M, N be positive real numbers and let ,
,  ,
,  and
and  be defined by (8), (9), (12), and (13),respectively.
be defined by (8), (9), (12), and (13),respectively.
It is easy to verify that

Moreover, the function  is decreasing with respect to m andc, and increasing with respect to b. Thus, from Theorems 1 and2 we have (see Figure 3)
is decreasing with respect to m andc, and increasing with respect to b. Thus, from Theorems 1 and2 we have (see Figure 3)

and

Therefore, by (4) we obtain

and by Theorem 2 we get (42). Putting  ,
,  in (3) we see that
in (3) we see that  are negative real numbers. Thus, the extremalfunction (40) has the form
are negative real numbers. Thus, the extremalfunction (40) has the form

or equivalently

Consequently, using (3) we obtain

that is, we have the function (43) and the proof is completed. □
Since  , by Theorem 1 we obtain the followingtheorem.
, by Theorem 1 we obtain the followingtheorem.
Theorem 4Let ,
,  , and
, and

where

Moreover, let us put

If , then the function
, then the function maps the disk
maps the disk onto a domain starlike with respect to the origin. The obtained resultis sharp for
onto a domain starlike with respect to the origin. The obtained resultis sharp for and for
and for the set ℬ cannot be larger then
the set ℬ cannot be larger then . It means that
. It means that

The function F of the form

is the extremal function.
Using (6) and Theorems 1-4, we obtain the radii of starlikeness for the classes ,
,  ,
,  ,
,  .
.
Corollary 1
The radius of starlikeness of the classes
 and
and
 is given by
is given by

Corollary 2
The radius of starlikeness of the class
 is given by
is given by

Corollary 3
The radius of starlikeness of the class
 is given by
is given by

Remark 1 Putting  in Corollary 3 we get the radius of starlikenessof the class
in Corollary 3 we get the radius of starlikenessof the class  obtained by Dziok [7]. Putting
obtained by Dziok [7]. Putting  we get the radius of starlikeness of the class
we get the radius of starlikeness of the class obtained by Ratti [9]. Putting, moreover,
obtained by Ratti [9]. Putting, moreover,  we get the radius of starlikeness of the class
we get the radius of starlikeness of the class obtained by MacGregor [10].
obtained by MacGregor [10].
References
Silverman H: Products of starlike and convex functions.Ann. Univ. Mariae Curie-Skłodowska, Sect. A 1975, 29:109–116.
Dimkov G: On products of starlike functions. I.Ann. Pol. Math. 1991, 55:75–79.
Aleksandrov IA: On the star-shaped character of the mappings of a domain by functions regular and univalent in the circle.Izv. Vysš. Učebn. Zaved., Mat. 1959,4(11):9–15.
Stankiewicz J, Świtoniak B: Generalized problems of convexity and starlikeness. In Complex Analysis and Applications. Publ. House Bulgar. Acad. Sci., Sofia; 1986:670–675. ’85 (Varna, 1985)
Świtoniak B:On a starlikeness problem in the class of functions
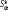 .Folia Sci. Univ. Tech. Resov. 1984, 14:17–27.
.Folia Sci. Univ. Tech. Resov. 1984, 14:17–27.Dimkov G, Dziok J: Generalized problem of starlikeness for products ofp-valentstarlike functions.Serdica Math. J. 1998, 24:339–344.
Dziok J: Generalized problem of starlikeness for products of close-to-starfunctions.Ann. Pol. Math. 2013, 107:109–121. 10.4064/ap107-2-1
Nunokawa M, Causey WM: On certain analytic functions bounded argument.Sci. Rep. Fac. Educ., Gunma Univ. 1985, 34:1–3.
Ratti JS: The radius of univalence of certain analytic functions.Math. Z. 1968, 107:241–248. 10.1007/BF01110013
MacGregor TH: The radius of univalence of certain analytic functions.Proc. Am. Math. Soc. 1963, 14:514–520. 10.1090/S0002-9939-1963-0148891-3
Acknowledgements
This work is partially supported by the Centre for Innovation and Transfer ofNatural Sciences and Engineering Knowledge, University of Rzeszów.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors jointly worked on the results and they read and approved the finalmanuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Arif, M., Dziok, J., Raza, M. et al. On products of multivalent close-to-star functions. J Inequal Appl 2015, 5 (2015). https://doi.org/10.1186/1029-242X-2015-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2015-5

 .
.

 and
and
 .
.

 and
and
 .
.
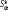 .Folia Sci. Univ. Tech. Resov. 1984, 14:17–27.
.Folia Sci. Univ. Tech. Resov. 1984, 14:17–27.