For convenience, we introduce an Appell sequence of polynomials (), defined by
If , we write . By [[1], Theorem 2.5.8] with , we have
More precisely, one can show that
where
Remember that the generalized Barnes-type Euler polynomials are defined by the generating function
If , then are called the Barnes-type Euler polynomials. If further , then are called the Euler polynomials of order s. If , we write . By [[1], Theorem 2.5.8] with , we have
We note that
From the definition (1), is the Sheffer sequence for the pair
So,
(12)
3.1 Explicit expressions
Let () with . The (signed) Stirling numbers of the first kind are defined by
Theorem 1
(13)
(14)
(15)
(16)
(17)
(18)
Proof Since
(19)
and
(20)
we have
So, we get (13).
We can obtain an alternative expression (14) for as follows:
From the proof of (13),
which is the identity (15).
By (12), we have
By (9), we get the identity (16).
Next,
Thus, we obtain (17).
Finally, we obtain
Thus, we get the identity (18). □
3.2 Sheffer identity
Theorem 2
(21)
Proof By (12) with
using (10), we have (21). □
3.3 Difference relations
Theorem 3
(22)
Proof By (8) with (12), we get
By (7), we have (22). □
3.4 Recurrence
Theorem 4
(23)
Proof By applying
(24)
[[1], Corollary 3.7.2] with (12), we get
Observe that
where
has the order at least one. Since from the proofs of (13) and (15)
we have
The third term is equal to
where , , and 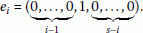 . The second term is
. The second term is
Therefore, we obtain
which is the identity (23). □
3.5 Differentiation
Theorem 5
(25)
Proof We shall use
(cf. [[1], Theorem 2.3.12]). Since
with (12), we have
which is the identity (25). □
3.6 One more relation
The classical Cauchy numbers of the first kind are defined by
(see e.g. [3, 4]).
Theorem 6
(26)
Proof For , we have
The third term is
Since
with
having order ≥1, the first term is
Since
the second term is
Therefore, we obtain
which is the identity (26). □
3.7 A relation involving the Stirling numbers of the first kind
Theorem 7 For , we have
(27)
Proof We shall compute
in two different ways. On the one hand, it is equal to
On the other hand, it is equal to
(28)
The third term of (28) is equal to
Since
the first term of (28) is equal to
The second term of (28) is equal to
Therefore, we get, for ,
Dividing both sides by m!, we obtain, for ,
Thus, we get (27). □
3.8 A relation with the falling factorials
Theorem 8
(29)
Proof For (12) and (20), assume that
By (11), we have
Thus, we get the identity (29). □
3.9 A relation with higher-order Frobenius-Euler polynomials
For with , the Frobenius-Euler polynomials of order r, are defined by the generating function
(see e.g. [5]).
Theorem 9
(30)
Proof For (12) and
(31)
assume that . By (11), similarly to the proof of (27), we have
Thus, we get the identity (30). □
3.10 A relation with higher-order Bernoulli polynomials
Bernoulli polynomials of order r are defined by
(see e.g. [[1], Section 2.2]). In addition, the Cauchy numbers of the first kind of order r are defined by
(see e.g. [[6], equation (2.1)], [[7], equation (6)]).
Theorem 10
(32)
Proof For (12) and
(33)
assume that . By (11), similarly to the proof of (27), we have
Thus, we get the identity (32). □
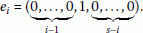 . The second term is
. The second term is