- Research
- Open access
- Published:
Some properties of the sequence space 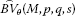
Journal of Inequalities and Applications volume 2013, Article number: 305 (2013)
Abstract
In this paper we define the sequence space  on a seminormed complex linear space by using an Orlicz function. We give various properties and some inclusion relations on this space.
on a seminormed complex linear space by using an Orlicz function. We give various properties and some inclusion relations on this space.
MSC:40A05, 40C05, 40D05.
1 Introduction
Let and c denote the Banach spaces of real bounded and convergent sequences normed by , respectively.
Let σ be a one-to-one mapping of the set of positive integers into itself such that , . A continuous linear functional φ on is said to be an invariant mean or a σ-mean if and only if
-
(i)
when the sequence has for all n,
-
(ii)
, where and
-
(iii)
for all .
If σ is the translation mapping , a σ-mean is often called a Banach limit [1], and , the set of σ-convergent sequences, that is, the set of bounded sequences all of whose invariant means are equal, is the set of almost convergent sequences [2].
If , set . It can be shown (see Schaefer [3]) that
where
The special case of (1.1), in which , was given by Lorentz [2].
Subsequently invariant means were studied by Ahmad and Mursaleen [4], Mursaleen [5], Raimi [6] and many others.
We may remark here that the concept  of almost bounded variation was introduced and investigated by Nanda and Nayak [7] as follows:
of almost bounded variation was introduced and investigated by Nanda and Nayak [7] as follows:

where
By a lacunary sequence , where , we shall mean an increasing sequence of non-negative integers with as . The intervals determined by θ will be denoted by , and we let . The ratio will usually be denoted by (see [8]).
Karakaya and Savaş [9] defined the sequence spaces  and
and  as follows:
as follows:

where
Straightforward calculation shows that
and
Note that for any sequences x, y and scalar λ, we have
An Orlicz function is a function , which is continuous, nondecreasing and convex with , for and as . (For details, see Krasnoselskii and Rutickii [10].)
It is well known that if M is a convex function and , then for all λ with .
Lindenstrauss and Tzafriri [11] used the idea of Orlicz function to construct the sequence space
The space is a Banach space with the norm
and this space is called an Orlicz sequence space. For , , the space coincides with the classical sequence space .
Definition 1.1 Any two Orlicz functions and are said to be equivalent if there are positive constants α and β, and such that for all x with (see Kamthan and Gupta [12]).
Later on, different types of sequence spaces were introduced by using an Orlicz function by Mursaleen et al. [13], Choudhary and Parashar [14], Tripathy and Mahanta [15] , Altinok et al. [16], Bhardwaj and Singh [17], Et et al. [18] and many others.
A sequence space E is said to be solid (or normal) if whenever for all sequences of scalars with .
It is well known that a sequence space E is normal implies that E is monotone.
Definition 1.2 Let , be seminorms on a vector space X. Then is said to be stronger than if whenever is a sequence such that , then also . If each is stronger than the others, and are said to be equivalent (one may refer to Wilansky [19]).
Lemma 1.3 Let and be seminorms on a linear space X. Then is stronger than if and only if there exists a constant T such that for all (see, for instance, Wilansky [19]).
Let be a sequence of strictly positive real numbers, X be a seminormed space over the field ℂ of complex numbers with the seminorm q, M be an Orlicz function and be a fixed real number. Then we define the sequence space  as follows:
as follows:

It is clear that for any seminorm q and any .
We get the following sequence spaces from by choosing some of the special p, M and s:
For we get

for , for all , we get

for we get

for and we get

for , for all , and we get

for , , for all , and we have
The following inequalities will be used throughout the paper. Let be a bounded sequence of strictly positive real numbers with , , then
where .
2 Main results
In this section we prove the general results of this paper on the sequence space  , those characterize the structure of this space.
, those characterize the structure of this space.
Theorem 2.1 The sequence space  is a linear space over the field ℂ of complex numbers.
is a linear space over the field ℂ of complex numbers.
Proof Omitted. □
Theorem 2.2 For any Orlicz function M and a bounded sequence of strictly positive real numbers,  is a paranormed space (not necessarily totally paranormed), paranormed by
is a paranormed space (not necessarily totally paranormed), paranormed by
where .
Proof Clearly . By using Theorem 2.1 and then using Minkowski’s inequality, we get .
Since and , we get for , where is the zero sequence of X.
Finally, we prove that scalar multiplication is continuous. Let λ be any numbers. By definition,
Then
where . Since , it follows that .
Hence
which converges to zero as converges to zero in  . Now suppose that and x is in . For arbitrary , let N be a positive integer such that
. Now suppose that and x is in . For arbitrary , let N be a positive integer such that
for some , all n. This implies that
for some , and all n.
Let , using convexity of M and all n, we get
Since M is continuous everywhere in , then
is continuous at 0. So there is such that for . Let K be such that for , then for , all n,
Thus
for and n, so that (). □
Theorem 2.3 Let M, , be Orlicz functions q, , seminorms and . Then
-
(i)
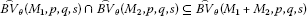 ,
, -
(ii)
If then
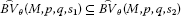 ,
, -
(iii)
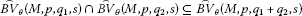 ,
, -
(iv)
If is stronger than , then
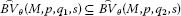 .
.
Proof Omitted □
Corollary 2.4 Let M be an Orlicz function, then we have
-
(i)
If (equivalent to) , then
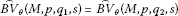 ,
, -
(ii)
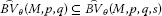 ,
, -
(iii)
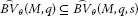 .
.
Theorem 2.5 Suppose that for each . Then  .
.
Proof Let  . Then there exists some such that
. Then there exists some such that
This implies that for sufficiently large values of k, say for some fixed . Since , for each we get
for all , and therefore
Hence we have
so  . This completes the proof. □
. This completes the proof. □
The following result is a consequence of the above result.
Corollary 2.6
-
(i)
If for each r, then
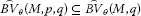 ,
, -
(ii)
If for all r, then
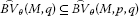 .
.
Theorem 2.7 Let and be any two of Orlicz functions. If and are equivalent, then  .
.
Proof Proof follows from Definition 1.1. □
Theorem 2.8 The sequence space  is solid.
is solid.
Proof Let  , i.e.,
, i.e.,
Let be sequence of scalars such that for all . Then the result follows from the following inequality:
□
Corollary 2.9 The sequence space  is monotone.
is monotone.
References
Banach S: Theorie des Operations Linearies. Subwncji Funduszu Narodowej, Warszawa; 1932.
Lorentz GG: A contribution the theory of divergent series. Acta Math. 1948, 80: 167–190. 10.1007/BF02393648
Schaefer P: Infinite matrices and invariant means. Proc. Am. Math. Soc. 1972, 36: 104–110. 10.1090/S0002-9939-1972-0306763-0
Ahmad ZU, Mursaleen M: An application of Banach limits. Proc. Am. Math. Soc. 1988, 103: 244–246. 10.1090/S0002-9939-1988-0938676-7
Mursaleen M: Matrix transformations between some new sequence spaces. Houst. J. Math. 1983, 9: 505–509.
Raimi RA: Invariant means and invariant matrix method of summability. Duke Math. J. 1963, 30: 81–94. 10.1215/S0012-7094-63-03009-6
Nanda S, Nayak KC: Some new sequence spaces. Indian J. Pure Appl. Math. 1978, 9(8):836–846.
Freedman AR, Sember JJ, Raphael M: Some Cesàro-type summability spaces. Proc. Lond. Math. Soc. 1978, 37(3):508–520.
Karakaya V, Savaş E: On almost p -bounded variation of lacunary sequences. Comput. Math. Appl. 2011, 61(6):1502–1506. 10.1016/j.camwa.2011.01.010
Krasnoselskii MA, Rutickii YB: Convex Functions and Orlicz Spaces. Noordhoff, Groningen; 1961.
Lindenstrauss J, Tzafriri L: On Orlicz sequence spaces. Isr. J. Math. 1971, 10: 379–390. 10.1007/BF02771656
Kamthan PK, Gupta M Lecture Notes in Pure and Applied Mathematics 65. In Sequence Spaces and Series. Dekker, New York; 1981.
Mursaleen M, Khan QA, Chishti TA: Some new convergent sequences defined by Orlicz functions and statistical convergence. Ital. J. Pure Appl. Math. 2001, 9: 25–32.
Choudhary B, Parashar SD: A sequence space defined by Orlicz functions. J. Approx. Theory Appl. 2002, 18(4):70–75.
Tripathy BC, Mahanta S:On a class of sequences related to the spaces defined by Orlicz function. Soochow J. Math. 2003, 29(4):379–391.
Altinok H, Altin Y, Işik M:The sequence space on seminormed spaces. Indian J. Pure Appl. Math. 2008, 39(1):49–58.
Bhardwaj VK, Singh N: On some new spaces of lacunary strongly σ -convergent sequences defined by Orlicz functions. Indian J. Pure Appl. Math. 2000, 31(11):1515–1526.
Et M, Altin Y, Choudhary B, Tripathy BC: On some classes of sequences defined by sequences of Orlicz functions. Math. Inequal. Appl. 2006, 9(2):335–342.
Wilansky A: Functional Analysis. Blaisdell Publishing Company, New York; 1964.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interest.
Authors’ contributions
MI, YA and ME have contributed to all parts of the article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Işik, M., Altin, Y. & Et, M. Some properties of the sequence space 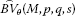 .
J Inequal Appl 2013, 305 (2013). https://doi.org/10.1186/1029-242X-2013-305
.
J Inequal Appl 2013, 305 (2013). https://doi.org/10.1186/1029-242X-2013-305
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-305
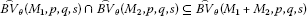 ,
,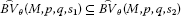 ,
,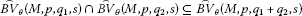 ,
,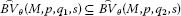 .
.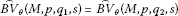 ,
,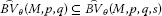 ,
,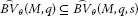 .
.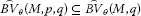 ,
,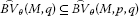 .
.