- Research
- Open access
- Published:
Inequality estimates for the boundedness of multilinear singular and fractional integral operators
Journal of Inequalities and Applications volume 2013, Article number: 303 (2013)
Abstract
In this paper, the inequality of boundedness for the multilinear fractional singular integral operators associated to the weighted Lipschitz functions is estimated. The operators include the Calderón-Zygmund singular integral operator and the fractional integral operator.
MSC:42B20, 42B25.
1 Introduction
As the development of the singular integral operators, their commutators and multilinear operators have been well studied (see [1–5]). In [1–3, 5–7], the authors proved that the commutators and multilinear operators generated by the singular integral operators and BMO functions are bounded on for . Chanillo (see [8]) proved a similar result when singular integral operators are replaced by the fractional integral operators. In [9–12], the boundedness for the commutators and multilinear operators generated by the singular integral operators and Lipschitz functions on () and Triebel-Lizorkin spaces are obtained. In [13, 14], the weighted boundedness for the commutators generated by the singular integral operators and BMO or Lipschitz functions on () spaces are obtained. The purpose of this paper is to study the weighted boundedness for some multilinear operators associated to the fractional singular integral operators and the weighted Lipschitz functions. As application, the weighted boundedness for the multilinear operators associated to the Calderón-Zygmund singular integral operator and the fractional integral operator is obtained.
2 Notations and theorems
In this paper, we are going to consider some multilinear operators as follows.
Let be positive integers (), , and let be locally integrable functions on (). Set
Definition 1 Let be a linear operator, and there exists a locally integrable function on such that
for every bounded and compactly supported function f, where K satisfies: for fixed and ,
and
Given bounded and compactly supported functions f defined on , the multilinear operator associated to T is defined by
Note that when , is just a multilinear commutator of T and b (see [15, 16]), while when , it is non-trivial generalization of the commutators; when , is just a multilinear commutator of the singular integral operator, when , is just a multilinear commutator of the fractional integral operator. It is well known that multilinear operators are of great interest in harmonic analysis and have been widely studied by many authors (see [1–4, 6, 7, 9, 10, 15, 16]). The purpose of this paper is to study the weighted boundedness properties for the multilinear operator.
Throughout this paper, Q will denote a cube of with sides parallel to the axes. For a cube Q and a locally integrable function f, let , and
It is well known that (see [17, 18])
For and , let
which is the Hardy-Littlewood maximal function when and .
The weight is defined by (see [17])
and . We know, for , w satisfies the double condition, that is, for any cube Q,
The weight is defined by (see [19])
Given a weight function w. For , the weighted Lebesgue space is the space of functions f such that
For and , let be the weighted homogeneous Triebel-Lizorkin space. For , the weighted Lipschitz space is the space of functions f such that
We shall prove the following theorems in Section 3.
Theorem 1 Suppose that is the multilinear operator as Definition 1 such that T is bounded from to for any , and . Let , , and for all α with and . Then is bounded from to for any and .
Theorem 2 Suppose that is the multilinear operator as Definition 1 such that T is bounded from to for any , and . Let , , and for all α with and . Then is bounded from to for any and .
3 Proofs of theorems
We begin with some preliminary lemmas.
Lemma 1 (see [1])
Let b be a function on and for and some . Then
where is the cube centered at x and having side length .
For , and , we have
Lemma 3 (see [8])
Suppose that , and . Then
For , and , we have
Lemma 5 (see [20])
For any cube Q, , and , we have
To prove the theorems, we need the following lemmas.
Key Lemma 1 Suppose that is the multilinear operator as Definition 1 such that T is bounded from to for any , and . Let , , and for all α with and . Then there exists a constant such that for every , and ,
Key Lemma 2 Suppose that is the multilinear operator as Definition 1 such that T is bounded from to for any , and . Let , , and for all α with and . Then there exists a constant such that for every , and ,
Proof of Key Lemma 1 Without loss of generality, we may assume . Fix a cube with . Let and , then and for . We split . Write
then
Now, let us estimate , , , and , respectively. First, by Lemmas 1 and 5, we get
Thus, by the -boundedness of T with and , we obtain
For , by the -boundedness of T with , and Lemma 5, we get
For , similar to the proof of , we get
Similarly, for , we obtain, for and ,
For , we write
Note that for and . By Lemmas 1 and 5, we get
Then, by the conditions on K, we obtain
For , by the formula (see [1])
and Lemma 5, we get
Similarly,
For , similar to the estimates of and , and noticing that for , and , by Lemma 4, we have
Thus, we obtain
Similarly,
For , we get
Thus
and
This completes the proof of the lemma. □
Proof of Key Lemma 2 Without loss of generality, we may assume . By using the same argument as in the proof of Key Lemma 1, we have
We obtain
For , similar to the proof of in Key Lemma 1, we obtain
Thus
This completes the proof of the lemma. □
Proof of Theorem 1 By Key Lemma 1, we get the sharp function estimate of as follows:
Now, choose in Key Lemma 1, by using Lemma 3 and notice that and . We get
This completes the proof of the theorem. □
Proof of Theorem 2 Choose in Key Lemma 2, notice that and . By using Lemmas 2 and 3, we obtain
This completes the proof of the theorem. □
4 Applications
In this section we shall apply Theorems 1 and 2 of the paper to some particular operators such as the Calderón-Zygmund singular integral operator and the fractional integral operator.
Application 1 Calderón-Zygmund singular integral operator.
Let T be the Calderón-Zygmund operator (see [17, 18]). The multilinear operator related to T is defined by
Then Theorem 1 holds for with .
Application 2 Fractional integral operator with rough kernel.
For , let be the fractional integral operator with rough kernel defined by (see [8, 17, 18])
which is the fractional integral operator when (see [8]). The multilinear operator related to is defined by
where Ω is homogeneous of degree zero on , and for some , that is, there exists a constant such that for any , . Then Theorem 2 holds for .
References
Cohen J:A sharp estimate for a multilinear singular integral on . Indiana Univ. Math. J. 1981, 30: 693–702. 10.1512/iumj.1981.30.30053
Cohen J, Gosselin J:On multilinear singular integral operators on . Stud. Math. 1982, 72: 199–223.
Cohen J, Gosselin J: A BMO estimate for multilinear singular integral operators. Ill. J. Math. 1986, 30: 445–465.
Coifman R, Meyer Y Cambridge Studies in Advanced Math. 48. In Wavelets, Calderón-Zygmund and Multilinear Operators. Cambridge University Press, Cambridge; 1997.
Coifman RR, Rochberg R, Weiss G: Factorization theorems for Hardy spaces in several variables. Ann. Math. 1976, 103: 611–635. 10.2307/1970954
Pérez C: Endpoint estimate for commutators of singular integral operators. J. Funct. Anal. 1995, 128: 163–185. 10.1006/jfan.1995.1027
Pérez C, Trujillo-Gonzalez R: Sharp weighted estimates for multilinear commutators. J. Lond. Math. Soc. 2002, 65: 672–692. 10.1112/S0024610702003174
Chanillo S: A note on commutators. Indiana Univ. Math. J. 1982, 31: 7–16. 10.1512/iumj.1982.31.31002
Chen WG: Besov estimates for a class of multilinear singular integrals. Acta Math. Sin. 2000, 16: 613–626. 10.1007/s101140000059
Ding Y, Lu SZ, Yabuta K: Multilinear singular and fractional integrals. Acta Math. Sin. 2006, 22: 347–356. 10.1007/s10114-005-0662-x
Janson S: Mean oscillation and commutators of singular integral operators. Ark. Mat. 1978, 16: 263–270. 10.1007/BF02386000
Paluszynski M: Characterization of the Besov spaces via the commutator operator of Coifman, Rochberg and Weiss. Indiana Univ. Math. J. 1995, 44: 1–17.
Bloom S: A commutator theorem and weighted BMO . Trans. Am. Math. Soc. 1985, 292: 103–122. 10.1090/S0002-9947-1985-0805955-5
Hu B, Gu J: Necessary and sufficient conditions for boundedness of some commutators with weighted Lipschitz spaces. J. Math. Anal. Appl. 2008, 340: 598–605. 10.1016/j.jmaa.2007.08.034
Pérez C, Pradolini G: Sharp weighted endpoint estimates for commutators of singular integral operators. Mich. Math. J. 2001, 49: 23–37. 10.1307/mmj/1008719033
Pérez C, Trujillo-Gonzalez R: Sharp weighted estimates for vector-valued singular integral operators and commutators. Tohoku Math. J. 2003, 55: 109–129. 10.2748/tmj/1113247449
Garcia-Cuerva J, Rubio de Francia JL North-Holland Mathematics Studies 116. In Weighted Norm Inequalities and Related Topics. North-Holland, Amsterdam; 1985.
Stein EM: Harmonic Analysis: Real Variable Methods, Orthogonality and Oscillatory Integrals. Princeton University Press, Princeton; 1993.
Muckenhoupt B, Wheeden RL: Weighted norm inequalities for fractional integral. Trans. Am. Math. Soc. 1974, 192: 261–274.
Garcia-Cuerva J Diss. Math. 162. Weighted
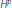 Spaces 1979.
Spaces 1979.
Acknowledgements
This work was jointly supported by the National Natural Science Foundation of China under Grant No. 11101053, the Key Project of Chinese Ministry of Education under Grant no. 211118, the Scientific Research Funds of Hunan Provincial Science and Technology Department of China no. 2013SK3143, the Hunan Provincial NSF no. 11JJ1001, the Scientific Research Fund of Hunan Provincial Education Department of China (no. 12C0028) and the Open Fund Project of Key Research Institute of Philosophies and Social Sciences in Hunan Universities (no. 12FEFM05).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
XZ carried out the Theorem 1 studies, participated in the disscussion of Theorem 2. CH is the corresponding author, designed the outline of this paper, carried out the Theorem 1 and Theorem 2 studies, participated in the disscussion of Applications. HH carried out the Theorem 2 studies, participated in the disscussion of Applications. LL participated in the disscussion of Applications and drafted the manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhou, X., Huang, C., Hu, H. et al. Inequality estimates for the boundedness of multilinear singular and fractional integral operators. J Inequal Appl 2013, 303 (2013). https://doi.org/10.1186/1029-242X-2013-303
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-303
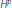 Spaces 1979.
Spaces 1979.