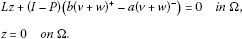Existence of four solutions for the elliptic problem with nonlinearity crossing one eigenvalue

Abstract

We investigate the multiplicity of the weak solutions for the nonlinear elliptic boundary value problem. We get a theorem which shows the existence of at least four weak solutions for the asymptotically linear elliptic problem with Dirichlet boundary condition. We obtain this result by using the Leray-Schauder degree theory, the variational reduction method and critical point theory.

MSC:35J15, 35J25.

1 Introduction

Let Ω be a bounded open subset of $R^n$ with smooth boundary ∂ Ω. Let L be the self-adjoint strongly elliptic partial differential operator

$$L=\sum _{1\le i,j\le n}\frac{\partial }{\partial x_i}{a}_{ij}(x)\frac{\partial }{\partial x_j},$$

where $a_{ij}(x)\in L^{\mathrm{\infty }}(\mathrm{\Omega })$. Let $f:R\to R$ be a $C^1$ function. Let ${\lambda }_k$ be the eigenvalues and ${\varphi }_k$, $k=1,2,\dots$ , be the associated normalized eigenfunctions of the eigenvalue problem $Lu+\lambda u=0$ in Ω, $u=0$ on ∂ Ω. We note that $0<{\lambda }_1<{\lambda }_2\le \cdots \le {\lambda }_k\to \mathrm{\infty }$ and ${\varphi }_1>0$.

In this paper, we consider the multiplicity of solutions of the following elliptic problem with Dirichlet boundary condition and jumping nonlinearity:

(1.1)

The physical model for this kind of the jumping nonlinearity problem can be furnished by traveling waves in suspension bridges. The nonlinear equations with jumping nonlinearity have been extensively studied by Lazer and McKenna [1], McKenna and Walter [2], Tarantello [3], Micheletti and Pistoia [4, 5], Jung and Choi [6–8] and many other authors. McKenna and Walter [2] proved that if $-\mathrm{\infty }<f^{\mathrm{\prime }}(-\mathrm{\infty })<{\lambda }_1$ and ${\lambda }_n<f^{\mathrm{\prime }}(+\mathrm{\infty })$, then there exists $s_0$ such that for all $s\ge s_0$, (1.1) has at least two solutions if n is odd, and three solutions if n is even.

Our main result is as follows.

Theorem 1.1 Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$, $s>0$. Then (1.1) has at least four solutions.

For the proof of Theorem 1.1 we use the Leray-Schauder degree theory, the variational reduction method and the critical point theory. The outline of this paper is as follows: In Section 2, we show the existence of the third weak solution for (1.1) by the variational reduction method and critical point theory. In Section 3, we show the existence of the fourth weak solution for (1.1) by the Leray-Schauder degree theory.

2 Existence of the third weak solution

We note that (1.1) has a positive solution $v_0=\frac{s{\varphi }_1}{b-{\lambda }_1}$ and a negative solution $v_1=\frac{s{\varphi }_1}{a-{\lambda }_1}$. To show the existence of the third solution of (1.1), we shall use the variational reduction method and the critical point theory. We assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ and $s>0$. Let $g(\xi )=b{\xi }^{+}-a{\xi }^{-}$ and $H_0^1(\mathrm{\Omega })$ be the Sobolev space with the norm

$${\parallel u\parallel }^2={\int }_{\mathrm{\Omega }}(-Lu)\cdot udx.$$

We consider the following functional associated with (1.1):

$$I_{a,b}(u,s)={\int }_{\mathrm{\Omega }}[-\frac{1}{2}Lu\cdot u-G(u)+s{\varphi }_{1}u]dx,$$

(2.1)

where

$$G(u)=\frac{b{|u^{+}|}^2}{2}+\frac{a{|u^{-}|}^2}{2}.$$

For simplicity, we shall write $I=I_{a,b}$ when a and b are fixed. By the condition $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ and $s>0$, I is well defined. By the following Lemma 2.1, $I(u,s)\in C(H_0^1(\mathrm{\Omega }),R)$ and Fréchet differentiable in $H_0^1(\mathrm{\Omega })$, so the solutions of (1.1) coincide with the critical points of $I(u,s)$.

Lemma 2.1 Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ and $s>0$. Then $I(u,s)$ is continuous and Fréchet differentiable in $H_0^1(\mathrm{\Omega })$ and

$$D_{u}I(u,s)(h)={\int }_{\mathrm{\Omega }}[-Lu\cdot h-(b{u}^{+}-a{u}^{-})h+s{\varphi }_{1}h]dx$$

for $h\in H_0^1(\mathrm{\Omega })$. Moreover, if we set

$$F(u,s)={\int }_{\mathrm{\Omega }}[\frac{b{|u^{+}|}^2}{2}+\frac{a{|u^{-}|}^2}{2}-s{\varphi }_{1}u]dx,$$

then $D_{u}F(u,s)$ is continuous with respect to weak convergence, $D_{u}F(u,s)$ is compact, and

$$D_{u}F(u,s)h={\int }_{\mathrm{\Omega }}[(b{u}^{+}-a{u}^{-})h-s{\varphi }_{1}h]dx\mathit{\text{for all}}h\in H_0^1(\mathrm{\Omega }).$$

This implies that $I\in C^1(H_0^1(\mathrm{\Omega }),R)$ and $F(u,s)$ is weakly continuous.

Proof Let $u\in H_0^1(\mathrm{\Omega })$. First, we will prove that $I(u,s)$ is continuous with respect to the variable u. We consider

$$|I(u+v,s)-I(u,s)|={\int }_{\mathrm{\Omega }}[u\cdot (-Lv)+\frac{1}{2}v\cdot (-Lv)-G(u+v)+G(u)]dx.$$

Let $u=\sum h_m{\varphi }_m$, $v=\sum {\tilde{h}}_m{\varphi }_m$. Then we have

On the other hand,

and hence

With the above results, we see that $I(u,s)$ is continuous at u. To prove $I(u,s)$ is Fréchet differentiable at $u\in H_0^1(\mathrm{\Omega })$, it is enough to compute the following:

$$\begin{array}{rcl}|I(u+v,s)-I(u,s)-D_{u}I(u,s)v|& =& |{\int }_{\mathrm{\Omega }}\frac{1}{2}v(-Lv)-G(u+v)+G(u)-g(u)v|\\ \le & \frac{1}{2}{\parallel v\parallel }^2+C\gamma \parallel v\parallel (\parallel u\parallel +\parallel v\parallel )+M\parallel v\parallel \\ \le & C^{\mathrm{\prime }}\parallel v\parallel (\parallel v\parallel +\parallel u\parallel +\parallel v\parallel +1).\end{array}$$

 □

Let V be the one-dimensional space spanned by the eigenfunction ${\varphi }_1$ whose eigenvalue is ${\lambda }_1$. Let W be the orthogonal complement of V in $H_0^1(\mathrm{\Omega })$. Let $P:H_0^1(\mathrm{\Omega })\to V$ be the orthogonal projection of $H_0^1(\mathrm{\Omega })$ onto V and $I-P:H_0^1(\mathrm{\Omega })\to W$ denote that of $H_0^1(\mathrm{\Omega })$ onto W. Then every element $u\in H_0^1(\mathrm{\Omega })$ is expressed by $u=v+z$, $v\in Pu$, $z=(I-P)u$. Then (2.1) is equivalent to the two systems in the two unknowns v and z:

(2.2)

(2.3)

The subspace W is spanned by eigenfunctions corresponding to the eigenvalues ${\lambda }_k$, $k\ge 2$. Let $v\in V$ be fixed and consider the function $h:W\to R$ defined by

$$h(w)=I(v+w,s).$$

The function h has continuous Fréchet derivatives Dh given by

$$Dh(w)(y)=D_{u}I(v+w,s)(y)$$

(2.4)

for $y\in W$. By Lemma 2.1, I is a function of class $C^1$.

By the following Lemma 2.2, we can get the critical points of the functional $I(u,s)$ on the infinite dimensional space $H_0^1(\mathrm{\Omega })$ from that of the reduced functional $\tilde{I}(v,s)$ on the finite dimensional subspace V.

Lemma 2.2 (Reduction Method)

Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ and $s>0$. Then

• (i) there exists a unique solution $z\in W$ of the equation

  

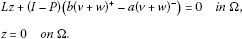
If we put $z=\theta (v,s)$, then θ is continuous on V and satisfies a uniform Lipschitz condition in v with respect to $L^2$ norm (also norm $\parallel \cdot \parallel$). Moreover,

$$D_{u}I(v+\theta (v,s),s)(w)=0\mathit{\text{for all}}w\in W.$$

• (ii) There exists $m>0$ such that if w and y are in W, then

  $$(Dh(w)-Dh(y))(w-y)\ge m{\parallel w-y\parallel }^2.$$

• (iii) If $\tilde{I}:V\to R$ is defined by $\tilde{I}(v,s)=I(v+\theta (v,s),s)$, then $\tilde{I}$ has a continuous Fréchet derivative $D_v\tilde{I}$ with respect to v, and

  $$D_v\tilde{I}(v,s)(h)=D_{u}I(v+\theta (v,s),s)(h)\mathit{\text{for all}}v,h\in V.$$

  (2.5)

• (iv) If $v_0\in V$ is a critical point of $\tilde{I}$ if and only if $v_0+\theta (v_0,s)$ is a critical point of I.

• (v) Let $S\subset V$ and $\mathrm{\Sigma }\subset H_0^1(\mathrm{\Omega })$ be open bounded regions such that

  $$\{v+\theta (v,s);v\in S\}=\mathrm{\Sigma }\cap \{v+\theta (v,s);v\in V\}.$$

If $D\tilde{I}(v,s)\ne 0$ for $v\in \partial S$, then

$$deg(D\tilde{I},S,0)=deg(DI,\mathrm{\Sigma },0),$$

where d denote the Leray-Schauder degree.

• (vi) If $u_0=v_0+\theta (v_0)$ is a critical point of mountain pass type of I, then $v_0$ is a critical point of mountain pass type of $\tilde{I}$.

Proof (i) Let $\delta =\frac{a+b}{2}$. If $g_1(\xi )=g(\xi )-\delta \xi$, then equation (2.3) is equivalent to

$$z={(-L-\delta )}^{-1}(I-P)(g_1(v+z)).$$

(2.6)

The operator ${(-L-\delta )}^{-1}(I-P)$ is self adjoint, compact and linear map from $(I-P)L^2(\mathrm{\Omega })$ into itself and its $L_2$ norm is ${|{\lambda }_2-\delta |}^{-1}$. Since $|g_1({\xi }_2)-g_1({\xi }_1)|\le max\{|a-\delta |,|b-\delta |\}|{\xi }_2-{\xi }_1|=\delta |{\xi }_2-{\xi }_1|$, it follows that the right-hand side of (2.6) defines, for fixed $v\in V$, a Lipschitz mapping of $(I-P)L^2(\mathrm{\Omega })$ into itself with Lipschitz constant $r=\frac{\delta }{|{\lambda }_2-\delta |}<1$. Therefore, by the contraction mapping principle, for given $v\in V$, there exists a unique $z=(I-P)L^2(\mathrm{\Omega })$ which satisfies (2.6). If $\theta (v,s)$ denote the unique $z\in (I-P)L^2(\mathrm{\Omega })$ which solves (2.3), then θ is continuous and satisfies a uniform Lipschitz condition in v with respect to $L^2$ norm (also norm $\parallel \cdot \parallel$). In fact, if $z_1=\theta (v_1,s)$ and $z_2=\theta (v_2,s)$, then

$$\begin{array}{rcl}{\parallel z_1-z_2\parallel }_{L^2(\mathrm{\Omega })}& =& {\parallel {(-L-\delta )}^{-1}(I-P)(g_1(v_1+z_1)-g_1(v_2+z_2))\parallel }_{L^2(\mathrm{\Omega })}\\ \le & r{\parallel (v_1+z_1)-(v_2+z_2)\parallel }_{L^2(\mathrm{\Omega })}\\ \le & r({\parallel v_1-v_2\parallel }_{L^2(\mathrm{\Omega })}+{\parallel z_1-z_2\parallel }_{L^2(\mathrm{\Omega })})\le r\parallel v_1-v_2\parallel +r\parallel z_1-z_2\parallel .\end{array}$$

Hence,

$$\parallel z_1-z_2\parallel \le C\parallel v_1-v_2\parallel ,C=\frac{r}{1-r}.$$

(2.7)

Let $u=v+z$, $v\in V$ and $z=\theta (v,s)$. If $w\in (I-P)L^2(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega })$,

$$\begin{array}{rcl}{D}_{u}I(v+\theta (v,s),s)(w)& =& {\int }_{\mathrm{\Omega }}[-L(v+z)\cdot w-Pg(v+z)w\\ -(I-P)g(v+w)w+s{\varphi }_{1}w]dx.\end{array}$$

From (2.3), we see that

$${\int }_{\mathrm{\Omega }}[(-Lz)\cdot w-(I-P)(g(v+z)w)]dx=0.$$

Since

$${\int }_{\mathrm{\Omega }}Lv\cdot w=0\text{and}{\int }_{\mathrm{\Omega }}[Pg(v+z)w-s{\varphi }_{1}w]dx=0,$$

we have

$$D_{u}I(v+\theta (v,s),s)(w)=0.$$

(2.8)

• (ii) If w and y are in W, then

  $$(Dh(w)-Dh(y))(w-y)={\int }_{\mathrm{\Omega }}[-L(w-y)(w-y)-(g(v+w)-g(v+y))(w-y)]dx.$$

Since ${\int }_{\mathrm{\Omega }}[-L(w-y)(w-y)]dx={\parallel w-y\parallel }^2$ and $(g({\xi }_2)-g({\xi }_1))({\xi }_2-{\xi }_1)<b{({\xi }_2-{\xi }_1)}^2$, we see that if w and y are in W, then ${\parallel w-y\parallel }_{L^2(\mathrm{\Omega })}\le \frac{1}{{\lambda }_2}{\parallel w-y\parallel }^2$ and

$${\int }_{\mathrm{\Omega }}[(g(v+w)-g(v+y))(w-y)]dx\le \frac{b}{{\lambda }_2}{\parallel w-y\parallel }^2$$

and

$$(Dh(w)-Dh(y))(w-y)\ge (1+b\frac{b}{{\lambda }_2}){\parallel w-y\parallel }^2,$$

where $(1+b\frac{b}{{\lambda }_2})>0$.

• (iii) Since the functional I has a continuous Fréchet derivative $D_{u}I$, $\tilde{I}$ has a continuous Fréchet derivative $D_v\tilde{I}$ with respect to v.

• (iv) Suppose that there exists $v_0\in V$ such that $D_v\tilde{I}(v_0,s)=0$. From $D_v\tilde{I}(v,s)(h)=D_{u}I(v+\theta (v,s),s)(h)$ for all $v,h\in V$, $D_{u}I(v_0+\theta (v_0,s),s)(h)=D_v\tilde{I}(v_0,s)(h)=0$ for all $h\in V$. Since $D_{u}I(v+\theta (v,s),s)(w)=0$ for all $w\in W$ and E is the direct sum of V and W, it follows that $D_{u}I(v_0+\theta (v_0,s),s)=0$. Thus, $v_0+\theta (v_0,s)$ is a solution of (1.1). Conversely, if u is a solution of (1.1) and $v=Pu$, then $D_v\tilde{I}(v)=0$.

• (v) The proof of part (v) follows by arguing as in Lemma 2.6 of [1].

• (vi) Suppose $v_0$ is not of mountain pass type of $\tilde{I}$. Let S be an open neighborhood of $v_0$ in V such that ${\tilde{I}}^{-1}(-\mathrm{\infty },\tilde{I}(v_0))\cap S$ is empty or path connected. If ${\tilde{I}}^{-1}(-\mathrm{\infty },\tilde{I}(v_0))\cap S$ is empty, by part (i) we see that $\{v+w:v\in V,w\in W\}\cap I^{-1}(-\mathrm{\infty },I(u_0))$ is also empty. Thus $u_0$ is not of mountain pass type for I. If ${\tilde{I}}^{-1}(-\mathrm{\infty },\tilde{I}(v_0))\cap S$ is path connected, Letting $T=\{v+w:v\in V,|\parallel w-\theta (v)|\parallel <1\}$ and using again (i) it is seen that $T\cap I^{-1}(-\mathrm{\infty },I(u_0))$ is also path connected. □

We define the functional on $H_0^1(\mathrm{\Omega })$

$$I_{a,b}^{\ast }(u)=I_{a,b}(u,0)={\int }_{\mathrm{\Omega }}[\frac{1}{2}(-Lu)\cdot u-\frac{b}{2}{\left|u^{+}\right|}^2-\frac{a}{2}{\left|u^{-}\right|}^2]dx.$$

The critical points of $I_{a,b}^{\ast }(u)$ coincide with the solutions of the equation

$$Lu+b{u}^{+}-a{u}^{-}=0\text{in }{H}_0^1(\mathrm{\Omega }).$$

(2.9)

Under the assumption $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$, (2.9) has only the trivial solution and hence $I_{a,b}^{\ast }(u)$ has only one critical point $u=0$. In fact, from (2.9), we obtain

$${\int }_{\mathrm{\Omega }}[(L+{\lambda }_1)u\cdot {\varphi }_1(x)+(b-{\lambda }_1)u^{+}{\varphi }_1(x)-(a-{\lambda }_1(x))u^{-}\cdot {\varphi }_1(x)]dx=0$$

(2.10)

under the assumption $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ the left-hand side of (2.10) is nonnegative, so the only possibility to hold (2.10) is that $u=0$. Given $v\in V$, let ${\theta }^{\ast }(v)=\theta (v,0)$ be the unique solution of the equation

$$Lz+(I-P)[b{(v+z)}^{+}-a{(v+z)}^{-}]=0\text{in }W.$$

Let us define ${\tilde{I}}_{a,b}^{\ast }(v)=I_{a,b}^{\ast }(v+{\theta }^{\ast }(v))$. We note that ${\tilde{I}}_{a,b}^{\ast }(v)$ has only the trivial critical point $v=0$.

Lemma 2.3 Let $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$. Then we have

$${\tilde{I}}_{a,b}^{\ast }(v)>0\mathit{\text{for all}}v\in V\mathit{\text{with}}v\ne 0.$$

Proof To prove the conclusion, it suffices to show that ${\tilde{I}}_{a,b}^{\ast }(v)$ does not satisfies the following cases:

• (i) ${\tilde{I}}_{a,b}^{\ast }(v)\le 0$ and ${\tilde{I}}_{a,b}^{\ast }(v_0)=0$ for some $v_0\in V$ with $v_0\ne 0$.

• (ii) ${\tilde{I}}_{a,b}^{\ast }(v)\ge 0$ and ${\tilde{I}}_{a,b}^{\ast }(v_1)=0$ for some $v_1\in V$ with $v_1\ne 0$.

• (iii) ${\tilde{I}}_{a,b}^{\ast }(v)<0$ for all $v\in V$ with $v\ne 0$.

• (iv) There exist $v_1$ and $v_2$ in V such that ${\tilde{I}}_{a,b}^{\ast }(v_1)<0$ and ${\tilde{I}}_{a,b}^{\ast }(v_2)>0$.

Suppose that (i) holds. It follows that ${\tilde{I}}_{a,b}^{\ast }(v)$ has an absolute maximum at $v_0$, and hence $D{\tilde{I}}_{a,b}^{\ast }(v_0)=0$. Therefore, by Lemma 2.2, $u_0=v_0+{\theta }^{\ast }(v_0)$ is a nontrivial solution of (2.9), which is a contradiction. A similar argument show that it is impossible that (ii) holds. Suppose that (iii) holds. Then there exists $t_0\in (0,1)$ such that for all t with $0<t\le t_0$,

$$t{\tilde{I}}_{a,b}^{\ast }(v)+(1-t){\tilde{I}}_{0,b}^{\ast }(v)\le 0\text{for all }v\ne 0.$$

We note that there exist $v_0\ne 0$ and t with $0<t\le t_0$ such that $t{\tilde{I}}_{a,b}^{\ast }(v_0)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_0)=0$ for some $v_0\ne 0$ and t. Let $t_1$ be the greatest number such that

$$t{\tilde{I}}_{a,b}^{\ast }(v_0)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_0)=0.$$

Then $0<t_1\le t_0$. Since $t_1{\tilde{I}}_{a,b}^{\ast }(v)+(1-t_1){\tilde{I}}_{0,b}^{\ast }(v)\le 0$ for all $v\ne 0$, and hence $v_0$ is a point of maximum of $t_1{\tilde{I}}_{a,b}^{\ast }(v)+(1-t_1){\tilde{I}}_{0,b}^{\ast }(v)$, we have

$$D[t_1{\tilde{I}}_{a,b}^{\ast }(v)+(1-t_1){\tilde{I}}_{0,b}^{\ast }(v)]=0.$$

Let $v\in V$ be given and $0<t_1<1$. Let ${\theta }_{t_1}^{\ast }(v)$ be the unique solution of the equation

$$Lz+(I-P)(b{u}^{+}-ta{u}^{-})=0\text{in }W.$$

By Lemma 2.2, $v_{0+{\theta }_{t_1}^{\ast }(v_0)}$ is a nontrivial solution of the equation

$$t_1(Lu+b{u}^{+}-a{u}^{-})+(1-t_1)(Lu+b{u}^{+}-a{u}^{-})=0\text{in }{H}_0^1(\mathrm{\Omega }),$$

that is,

$$Lu+b{u}^{+}-t_{1}a{u}^{-}=0\text{in }{H}_0^1(\mathrm{\Omega }),$$

which contradicts the fact that the above equation has only the trivial solution because $-\mathrm{\infty }<t_{1}a<{\lambda }_1<b<{\lambda }_2$. Suppose that (iv) holds. Since the equation (2.9) has only the trivial solution, $I_{a,b}^{\ast }(u)$ has only one critical point $u=0$. By the assumption (iv), the trivial solution $u=0$ is a point of inflexion, and hence by Lemma 2.2, $v=0$ is the critical point of ${\tilde{I}}_{a,b}^{\ast }(v)$, which is a point of inflexion. By the assumption (iv), there exist $v_3$, $v_4$ in V and $t_0\in (0,1)$ such that for all t with $0<t\le t_0$, $t{\tilde{I}}_{a,b}^{\ast }(v_3)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_3)<0$ and $t{\tilde{I}}_{a,b}^{\ast }(v_4)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_4)>0$. We note that there exists t with $0<t\le t_0$ such that $t{\tilde{I}}_{a,b}^{\ast }(v_3)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_3)<0$ and $t{\tilde{I}}_{a,b}^{\ast }(v_4)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_4)>0$. Let $t_1$ be the greatest number such that

$$t{\tilde{I}}_{a,b}^{\ast }(v_3)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_3)<0\text{and}t{\tilde{I}}_{a,b}^{\ast }(v_4)+(1-t){\tilde{I}}_{0,b}^{\ast }(v_4)>0.$$

Then $0<t_1\le t_0$. Since $t_1{\tilde{I}}_{a,b}^{\ast }(v_3)+(1-t_1){\tilde{I}}_{0,b}^{\ast }(v_3)<0$ and $t_1{\tilde{I}}_{a,b}^{\ast }(v_4)+(1-t_1){\tilde{I}}_{0,b}^{\ast }(v_4)>0$. Thus, there exists a point of inflexion $v_0\ne 0$ of $t_1{\tilde{I}}_{a,b}^{\ast }(v)+(1-t_1){\tilde{I}}_{0,b}^{\ast }(v)$ and we have

$$D{t}_1{\tilde{I}}_{a,b}^{\ast }(v)+(1-t_1){\tilde{I}}_{0,b}^{\ast }(v_0)=0.$$

Let $v\in V$ be given and $0<t_1<1$. Let ${\theta }_{t_1}^{\ast }(v)$ be the unique solution of the equation

$$Lz+(I-P)(b{u}^{+}-ta{u}^{-})=0\text{in }W.$$

By Lemma 2.2, $v_0+{\theta }_{t_1}^{\ast }(v_0)$ is a nontrivial solution of the equation

$$t_1(Lu+b{u}^{+}-a{u}^{-})+(1-t_1)(Lu+b{u}^{+}-a{u}^{-})=0\text{in }{H}_0^1(\mathrm{\Omega }),$$

that is,

$$Lu+b{u}^{+}-t_{1}a{u}^{-}=0\text{in }{H}_0^1(\mathrm{\Omega }),$$

which contradicts the fact that the above equation has only the trivial solution because $-\mathrm{\infty }<t_{1}a<{\lambda }_1<b<{\lambda }_2$. □

From now on, we shall denote that $I_{a,b}=I$.

Lemma 2.4 Let $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$. Then we have

$${\tilde{I}}_{a,b}(v,s)\to \mathrm{\infty }\mathit{\text{as}}\parallel v\parallel \to \mathrm{\infty }.$$

Proof We shall prove the lemma by contradiction. We suppose that there exists a sequence ${\{v_n\}}_1^{\mathrm{\infty }}$ in V and a number $M>0$ such that $\parallel v_n\parallel \to \mathrm{\infty }$ as $n\to \mathrm{\infty }$ and $\tilde{I}(v_n,s)\le M$. For given $v_n\in V$, let $w_n=\theta (v_n,s)$ be the unique solution of the equation

$$Lw+(I-P)(b{(v_n+w)}^{+}-a{(v_n+w)}^{-}-s{\varphi }_1-h(x))=0\text{in }W.$$

By Lemma 2.2, we have that for some constant k,

$$\parallel \theta (v_n)-\theta (0)\parallel \le k\parallel v_n\parallel .$$

From this the sequence $\{\frac{\parallel v_n+w_n\parallel }{\parallel v_n\parallel }\}$ is bounded in H. Let $u_n=v_n+w_n$, $v_n^{\ast }=\frac{v_n}{\parallel v_n\parallel }$, $w_n^{\ast }=\frac{w_n}{\parallel v_n\parallel }$ and $u_n^{\ast }=v_n^{\ast }+w_n^{\ast }$ for $n\ge 1$. For $w_n=\theta (v_n,s)$ and $w_n^{\ast }=\frac{w_n}{\parallel v_n\parallel }$, we have

$$w_n^{\ast }=L^{-1}((I-P)(-b\frac{{(v_n+w_n)}^{+}}{\parallel v_n\parallel }+a\frac{{(v_n+w_n)}^{-}}{\parallel v_n\parallel }-s\frac{{\varphi }_1}{\parallel v_n\parallel }-\frac{h(x)}{\parallel v_n\parallel }))\text{in }W.$$

Since $\{\frac{v_n+w_n}{\parallel v_n\parallel }\}$ is bounded and $\frac{{\varphi }_1}{\parallel v_n\parallel }\to 0$, $-b\frac{{(v_n+w_n)}^{+}}{\parallel v_n\parallel }+a\frac{{(v_n+w_n)}^{-}}{\parallel v_n\parallel }-s\frac{{\varphi }_1}{\parallel v_n\parallel }-\frac{h(x)}{\parallel v_n\parallel }$ is bounded in H. Since $L^{-1}$ is a compact operator, by passing to a subsequence, we get that ${\{w_n^{\ast }\}}_1^{\mathrm{\infty }}$ converges to $w^{\ast }$. Since V is 1-dimensional subspace, we may assume that ${\{v_n^{\ast }\}}_1^{\mathrm{\infty }}$ converges to $v^{\ast }\in V$ with $\parallel v^{\ast }\parallel =1$. Therefore, ${\{u_n^{\ast }\}}_1^{\mathrm{\infty }}$ converges to $u^{\ast }$ in $H_0^1(\mathrm{\Omega })$. Since $\tilde{I}(v_n,s)\le M$ for all n, we have, for all n,

$${\int }_{\mathrm{\Omega }}[-\frac{1}{2}L{u}_n\cdot u_n-\frac{b}{2}{\left|u_n^{+}\right|}^2-\frac{a}{2}{\left|u_n^{-}\right|}^2+s{\varphi }_1{u}_n+h(x)u_n]dx\le M.$$

Dividing the above inequality by ${\parallel v_n\parallel }^2$, we obtain

(2.11)

From the definition of $w_n=\theta (v_n,s)$, we have that for any $y\in W$, $n\ge 1$,

$${\int }_{\mathrm{\Omega }}[L{u}_n\cdot y+b{u}_n^{+}y-a{u}_n^{-}y-s{\varphi }_{1}y-h(x)y]dx=0.$$

(2.12)

Let us set $y=w_n$ in (2.12) and divide by ${\parallel v_n\parallel }^2$. Then we have

$${\int }_{\mathrm{\Omega }}[L{u}_n^{\ast }\cdot w_n^{\ast }+b{\left(u_n^{\ast }\right)}^{+}{w}_n^{\ast }-a{\left(u_n^{\ast }\right)}_n^{-}{w}_n^{\ast }-s{\varphi }_1\frac{w_n^{\ast }}{\parallel v_n\parallel }-h(x)\frac{w_n^{\ast }}{\parallel v_n\parallel }]dx=0$$

(2.13)

for all $n\ge 1$. Let $y\in W$. Dividing (2.12) by $\parallel v_n\parallel$ and letting $n\to \mathrm{\infty }$, we obtain

$${\int }_{\mathrm{\Omega }}[L{u}^{\ast }\cdot y+b{\left(u^{\ast }\right)}^{+}y-a{\left(u^{\ast }\right)}^{-}y-s{\varphi }_{1}y-h(x)y]dx=0.$$

(2.14)

(2.14) can be rewritten in the form

$$D{\tilde{I}}_{a,b}^{\ast }(v^{\ast }+w^{\ast })(y)=0\text{for all }y\in W.$$

By $w^{\ast }=\theta (v^{\ast })$, letting $n\to \mathrm{\infty }$ in (2.13), we have

$$\begin{array}{rcl}\underset{n\to \mathrm{\infty }}{lim}{\int }_{\mathrm{\Omega }}L{w}_n^{\ast }\cdot w_n^{\ast }dx& =& -{\int }_{\mathrm{\Omega }}[b{u}^{\ast }{w}^{\ast }-a{u}^{\ast }{w}^{\ast }]dx\\ =& {\int }_{\mathrm{\Omega }}[L{u}^{\ast }\cdot w^{\ast }]dx={\int }_{\mathrm{\Omega }}[L{w}^{\ast }\cdot w^{\ast }]dx.\end{array}$$

Hence,

$$\underset{n\to \mathrm{\infty }}{lim}{\int }_{\mathrm{\Omega }}L{u}_n^{\ast }\cdot u_n^{\ast }dx={\int }_{\mathrm{\Omega }}[L{u}^{\ast }\cdot u^{\ast }]dx.$$

Letting $n\to \mathrm{\infty }$ in (2.11), we obtain

$${\tilde{I}}_{a,b}^{\ast }\left(v^{\ast }\right)={\int }_{\mathrm{\Omega }}[-\frac{1}{2}L{u}^{\ast }\cdot u^{\ast }-\frac{b}{2}{\left|{\left(u^{\ast }\right)}^{+}\right|}^2-\frac{a}{2}{\left|{\left(u^{\ast }\right)}^{-}\right|}^2]dx\le 0.$$

Since $\parallel v^{\ast }\parallel =1$, this contradicts the fact that ${\tilde{I}}^{\ast }(v)>0$ for all $v\ne 0$. Thus, $\tilde{I}(v,s)\to \mathrm{\infty }$ as $\parallel v\parallel \to \mathrm{\infty }$. □

Lemma 2.5 Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ and $s>0$. Then there exists a small open neighborhood B of $v_0$ in V such that $v_0$ is a strict local point maximum of $\tilde{I}(v,s)$ and there exists a small open neighborhood D of $v_1$ in V such that $v_1$ is a strict point of minimum of $\tilde{I}(v,s)$, where $v_0=\frac{s{\varphi }_1}{b-{\lambda }_1}$ is a positive solution and $v_1=\frac{s{\varphi }_1}{a-{\lambda }_1}$ is a negative solution of (1.1).

Proof Since the positive solution $v_0=\frac{s{\varphi }_1}{b-{\lambda }_1}$ is in V, $\theta (v_0,s)=0$ and $I+\theta$, where I is an identity map on V, is continuous on V, it follows that there exists a small open neighborhood B of $v_0$ in V such that if $v_0+v\in B$, then $v_0+v+\theta (v_0+v,s)>0$. Here, $\theta (v_0+v,s)=\theta (v_0,s)=0$. Therefore, if $v_0+v\in B$, then for $z=\theta v_0+v,s=\theta (v_0)=0$, we have

$$\begin{array}{rcl}\tilde{I}(v_0+v,s)& =& I(v_0+v,s)\\ =& {\int }_{\mathrm{\Omega }}[-\frac{1}{2}L(v_0+v)\cdot (v_0+v)-\frac{b{|v_0+v|}^2}{2}+s{\varphi }_1(v_0+v)]dx\\ =& {\int }_{\mathrm{\Omega }}[-\frac{1}{2}Lv\cdot v-\frac{b{|v|}^2}{2}]dx+C,\end{array}$$

where

$$C={\int }_{\mathrm{\Omega }}[-\frac{1}{2}L{v}_0\cdot v_0-\frac{b{|v_0|}^2}{2}+s{\varphi }_1{v}_0]dx=I(v_0,s)=\tilde{I}(v_0,s).$$

Each $v\in V$ has the form $v=c{\varphi }_1$ Therefore, we have, in B,

Since ${\lambda }_1<b<{\lambda }_2$, $v_0$ is a strict local point maximum of $\tilde{I}(v,s)$. Since the negative solution $v_1=\frac{s{\varphi }_1}{a-{\lambda }_1}$ is in V, $\theta (v_1,s)=0$ and $I+\theta$, where I is an identity map on V, is continuous on V, it follows that there exists a small open neighborhood D of $v_1$ in V such that if $v_1+v\in B$, then $v_1+v+\theta (v_1+v,s)<0$. Here, $\theta (v_1+v,s)=\theta (v_1,s)=0$. Therefore, if $v_1+v\in B$, then for $z=\theta v_1+v,s=\theta (v_1,s)=0$, we have

$$\begin{array}{rcl}\tilde{I}(v_1+v,s)& =& I(v_1+v,s)={\int }_{\mathrm{\Omega }}[-\frac{1}{2}L(v_1+v)\cdot (v_1+v)-\frac{a{|v_1+v|}^2}{2}+s{\varphi }_1(v_1+v)]dx\\ =& {\int }_{\mathrm{\Omega }}[-\frac{1}{2}Lv\cdot v-\frac{a{|v|}^2}{2}]dx+C_1,\end{array}$$

where

$$\begin{array}{rcl}{C}_1& =& {\int }_{\mathrm{\Omega }}[-\frac{1}{2}L{v}_1\cdot v_1-\frac{a{|v_1|}^2}{2}+s{\varphi }_1{v}_1]dx\\ =& I(v_1,s)=\tilde{I}(v_1,s).\end{array}$$

Each $v\in V$ has the form $v=c{\varphi }_1$ Therefore, we have, in B,

since $-\mathrm{\infty }<a<{\lambda }_1$. Thus, $v_1$ is a strict local point minimum of $\tilde{I}(v,s)$. □

Lemma 2.6 (Existence of the Third Solution)

Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ and $s>0$. Then (1.1) has the third weak solution which is a strict point of minimum of $I_{a,b}(u,s)$.

Proof We know that (1.1) has a positive solution $v_0=\frac{s{\varphi }_1}{b-{\lambda }_1}$ and a negative solution $v_1=\frac{s{\varphi }_1}{a-{\lambda }_1}$. By Lemma 2.2 (reduction method), we shall show the existence of the third weak solution of (1.1). By Lemma 2.1, $\tilde{I}(v,s)$ is continuous and Fréchet differentiable. By Lemma 2.4, $\tilde{I}(v,s)\to \mathrm{\infty }$ as $\parallel v\parallel \to \mathrm{\infty }$, so $\tilde{I}(v,s)$ is bounded from below, satisfies the (P.S.) condition. By Lemma 2.5, there exists a small open neighborhood B of $v_0$ in V such that $v_0$ is a strict local point of maximum of $\tilde{I}(v,s)$ and there exists a small open neighborhood D of $v_1$ in V such that $v_1$ is a strict local point of minimum of $\tilde{I}(v,s)$. By the shape of the graph of the functional $\tilde{I}$ on the 1-dimensional subspace V, there exists the third critical point $v_2\ne 0$ which is a strict local point of minimum of $\tilde{I}(v,s)$. By Lemma 2.2, $v_2+\theta (v_2,s)$ is a solution of (1.1) and a strict local point of minimum of $I_{a,b}(u,s)$. □

3 Existence of the fourth weak solution

In this section, we shall consider the Leray-Schauder degree of the elliptic operator for the multiplicity of the solutions of (1.1).

Lemma 3.1 Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$. Then there exists $s_1>0$, $ϵ>0$ such that the Leray-Schauder degree

$$deg(u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1),B_{ϵs}^{\ast }(v_0),0)=-1$$

(3.1)

for $s\ge s_1$. Here, $B_{\tau }^{\ast }$ denotes a ball of radius τ in $H_0^1(\mathrm{\Omega })$ and $v_0=\frac{s{\varphi }_1}{b-{\lambda }_1}$ is a positive solution of (1.1).

The proof of this lemma has the similar process to that of Theorem 1 in [2].

Lemma 3.2 If $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$, then there exist positive constants $s_2$, ϵ such that

$$deg(u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1),B_{ϵs}^{\ast }(v_1),0)=1$$

for $s\ge s_2$, where $v_1=\frac{s{\varphi }_1}{a-{\lambda }_1}$ is a negative solution of (1.1).

The proof of this lemma has the same process as that of Lemma 3.1.

Lemma 3.3 If $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$, then there exist positive constants $s_3$, $\gamma >0$ such that

$$deg(u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1),B_{\gamma }^{\ast }(v_2),0)=1$$

for $s\ge s_3$, where $v_2$ is the third solution of (1.1).

Proof We know that the third solution $v_2$ of (1.1) is an isolated local minimum of $I_{a,b}(u,s)$. By [9], there exist positive constants $s_3$, $\gamma >0$ such that

$$deg(D\tilde{I},B_{\gamma }^{\ast }(v_2)\cap V,0)=1$$

for $s\ge s_3$, where $B_{\gamma }^{\ast }(v_2)\cap V$ is a ball centered at 0 containing no other critical point. By (v) of Lemma 2.2,

$$deg(u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1),B_{\gamma }^{\ast }(v_2),0)=deg(D\tilde{I},B_{\gamma }^{\ast }(v_2)\cap V,0)=1.$$

So we prove the lemma. □

Lemma 3.4 Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$ and s is bounded. Then there exist C and $s^{\ast }>0$ such that any solution to (1.1) satisfies $\parallel u\parallel \le C$ for any s with $s\le s^{\ast }$.

Proof If not, then there exist $(u_n,s_n)$ with $\parallel u_n\parallel \to \mathrm{\infty }$, $s_n\to s^{\ast }$, $s_n$ is bounded, which satisfy equation (1.1). Now let $v_n=\frac{u_n}{\parallel u_n\parallel }$, and $v_n$ satisfies

$$L{v}_n+(b{v}_n^{+}-a{v}_n^{-})-\frac{s_n{\varphi }_1(x)}{\parallel u_n\parallel }=0.$$

(3.2)

Taking the inner product of both sides of (3.2) with ${\varphi }_1$, we have

$$0=〈-L{v}_n-{\lambda }_1{v}_n,{\varphi }_1〉=〈(b-{\lambda }_1)v_n^{+}+({\lambda }_1-a)v_n^{-},{\varphi }_1〉-〈\frac{s_n{\varphi }_1(x)}{\parallel u_n\parallel },{\varphi }_1〉.$$

(3.3)

Thus,

$$\left|〈\frac{s_n{\varphi }_1(x)}{\parallel u_n\parallel },{\varphi }_1〉\right|\ge ϵ\int |v_n|{\varphi }_1(x)\ge ϵ|\int v_n{\varphi }_1(x)|.$$

Thus, if $v_n$ is a solution of (3.3), then

$$\left|〈v_n,{\varphi }_1(x)〉\right|\le \frac{1}{ϵ}\left|〈\frac{s_n{\varphi }_1(x)}{\parallel u_n\parallel },{\varphi }_1(x)〉\right|.$$

(3.4)

Since $v_n$’s are precompact in $H_0^1(\mathrm{\Omega })$, there exists v with $\parallel v\parallel =1$ such that $v_n\to v$. Taking the limit of both sides of (3.4), we have

$$\left|〈v,{\varphi }_1(x)〉\right|\le 0.$$

Thus, we have

$$\left|〈v,{\varphi }_1(x)〉\right|=0,$$

and hence $v=0$. This is impossible, since $\parallel v\parallel =1$. □

We have the following no solvability condition for (1.1).

Lemma 3.5 Assume that $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$. Then there exists a constant $s_0<0$ so small enough that if $s\le s_0$, the problem

$$-Lu=b{u}^{+}-a{u}^{-}-s{\varphi }_1\mathit{\text{in}}{H}_0^1(\mathrm{\Omega })$$

has no solution.

Proof We can rewrite (1.1) as

$$(-L-{\lambda }_1)u=-{\lambda }_1{u}^{+}+b{u}^{+}+({\lambda }_1-a)u^{-}-s{\varphi }_1.$$

(3.5)

Taking the inner product of both sides of (3.5) with ${\varphi }_1$, we have

$$0=〈-({\lambda }_1-b)u^{+}+({\lambda }_1-a)u^{-}-s{\varphi }_1,{\varphi }_1〉\ge -s.$$

Thus, there is no solution for $s\le s_0$ if $s_0<0$. This completes the proof. □

Lemma 3.6 Let $-\mathrm{\infty }<a<{\lambda }_1<b<{\lambda }_2$. Then there exists $\beta >0$, depending on C and $s^{\ast }$ such that

$$deg(u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1),B_{\beta }^{\ast }(0),0)=0$$

for $s\le s^{\ast }$ and $\beta >C$.

Proof By Lemma 3.5, there exists a constant $s_0<0$ so small enough that if $s\le s_0$, (1.1) has no solution. By Lemma 3.4, there exist a constant C and $s^{\ast }>0$ such that if u is a solution of (1.1) with $s\le s^{\ast }$, then $\parallel u\parallel \le C$. Let us choose β so large that $\beta >C$. We note that

$$u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1)\ne 0\text{on }\partial B_{\beta }^{\ast }(0)$$

and

$$u-L^{-1}(-b{u}^{+}+a{u}^{-}+s_0{\varphi }_1+\lambda (s-s_0){\varphi }_1(x))\ne 0\text{on }\partial B_{\beta }^{\ast }(0)$$

for $0\le \lambda \le 1$. By the homotopy invariance property, we have that the Leray-Schauder degree

where $s\le s^{\ast }$ and $0\le \lambda \le 1$. Thus, we proved the lemma. □

Proof of Theorem 1.1 By Lemma 3.4 and Lemma 3.6, there exists a large number $\beta >0$ (depending on C and $s^{\ast }$) such that all solutions of (1.1) are contained in the ball $B_{\beta }(0)$ and the Leray-Schauder degree

$$deg(u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1),B_{\beta }^{\ast }(0),0)=0$$

for $\beta >C$ and $0<s<s^{\ast }$. Let us choose a positive number $s^{\ast }$ such that $s_{\ast }=max\{s_1,s_2,s_3\}$ and $s_{\ast }<s^{\ast }$. Then by Lemma 3.1, Lemma 3.2 and Lemma 3.3, for all s with $s_{\ast }\le s\le s^{\ast }$, there exist three disjoint balls $B_{ϵs}^{\ast }(v_0)$, $B_{ϵs}^{\ast }(v_1)$ and $B_{\gamma }^{\ast }(v_2)$ such that

By the excision property of Leray-Schauder degree,

$$deg(u-L^{-1}(-b{u}^{+}+a{u}^{-}+s{\varphi }_1),B_{\beta }^{\ast }(0)\mathrm{\setminus }\left\{B_{ϵs}^{\ast }\right(v_0\cup B_{ϵs}^{\ast }(v_1)\cup B_{\gamma }^{\ast }(v_2)\},0)=-1.$$

Thus, (1.1) has at least four solutions. □