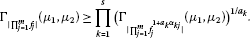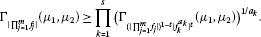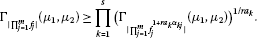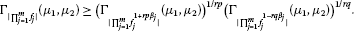Generalizations of Hölder inequalities for Csiszar’s f-divergence

Abstract

In this paper, we establish some new generalizations of the Hölder’s inequality involving Csiszar’s f-divergence of two probability measures. Some related inequalities are also presented.

MSC:26D15, 28A25, 60E15.

1 Introduction

Let $1/p+1/q=1$, assume that $f(x)$ and $g(x)$ are continuous real-valued functions on $[a,b]$. Then

• (1) for $p>1$, we have the following Hölder inequality (see [1]):

  $${\int }_a^{b}f(x)g(x)dx\le {({\int }_a^b{f}^p(x)dx)}^{1/p}{({\int }_a^b{g}^q(x)dx)}^{1/q};$$

  (1.1)

• (2) for $0<p<1$, we have the following reverse Hölder inequality (see [2]):

  $${\int }_a^{b}f(x)g(x)dx\ge {({\int }_a^b{f}^p(x)dx)}^{1/p}{({\int }_a^b{g}^q(x)dx)}^{1/q}.$$

  (1.2)

The above inequalities play an important role in many areas of pure and applied mathematics. A large number of generalizations, refinements, variations and applications of (1.1) and (1.2) have been investigated in the literature (see [3–11] and references therein). Recently, G.A. Anastassiou [12] established some Hölder’s type inequalities regarding Csiszar’s f-divergence of two probability measures as follows.

Theorem 1.1 (see [12])

Let $p,q>1$ such that $1/p+1/q=1$. Then

$${\mathrm{\Gamma }}_{|f_1{f}_2|}({\mu }_1,{\mu }_2)\le {[{\mathrm{\Gamma }}_{|f_1{|}^p}({\mu }_1,{\mu }_2)]}^{1/p}{[{\mathrm{\Gamma }}_{|f_2{|}^q}({\mu }_1,{\mu }_2)]}^{1/q}.$$

(1.3)

Theorem 1.2 (see [12])

Let $a_1,a_2,\dots ,a_m>1$, $m\in \mathrm{N}$, ${\sum }_{j=1}^m\frac{1}{a_j}=1$. Then

(1.4)

which is a generalization of Theorem 1.1.

It follows the counterpart of Theorem 1.1.

Theorem 1.3 (see [12])

Let $0<p<1$ and $q<0$ such that $1/p+1/q=1$, we assume that $p_2>0$ a.e. $[\lambda ]$. Then we have

$${\mathrm{\Gamma }}_{|f_1{f}_2|}({\mu }_1,{\mu }_2)\ge {[{\mathrm{\Gamma }}_{|f_1{|}^p}({\mu }_1,{\mu }_2)]}^{1/p}{[{\mathrm{\Gamma }}_{|f_2{|}^q}({\mu }_1,{\mu }_2)]}^{1/q}.$$

(1.5)

The aim of this paper is to give new generalizations of inequalities (1.4) and (1.5). Some related inequalities are also considered. The paper is organized as follows. In Section 2, we recall some basic facts about the Csiszar’s f-divergence of two probability measures. In Section 3, we will give the main result and its proof.

2 Preliminaries

Assume that $f:(0,+\mathrm{\infty })\to \mathrm{R}$ is an arbitrary convex function which is strictly convex at 1. As in Csiszar [12, 13], we agree with the following expressions:

Suppose that $(X,A,\lambda )$ is an arbitrary measure space with λ being a finite or σ-finite measure. Let ${\mu }_1$, ${\mu }_2$ be probability measures on X such that ${\mu }_1,{\mu }_2\ll \lambda$ (absolutely continuous).

The Radon-Nikodym derivatives (densities) of ${\mu }_i$ with respect to λ is expressed by $p_i(x)$:

$$p_i(x)=\frac{{\mu }_i(dx)}{\lambda (dx)},i=1,2.$$

Definition 2.1 (see [13])

The f-divergence of the probability measures ${\mu }_1$ and ${\mu }_2$ is defined as follows:

$${\mathrm{\Gamma }}_f({\mu }_1,{\mu }_2)={\int }_X{p}_2(x)f\left(\frac{p_1(x)}{p_2(x)}\right)\lambda (dx),$$

where the function f is named the base function. From Lemma 1.1 of [13], ${\mathrm{\Gamma }}_f({\mu }_1,{\mu }_2)$ is always well-defined and ${\mathrm{\Gamma }}_f({\mu }_1,{\mu }_2)\ge f(1)$ with equality only for ${\mu }_1={\mu }_2$. From [13], we know that ${\mathrm{\Gamma }}_f({\mu }_1,{\mu }_2)$ does not depend on the choice of λ. If $f(1)=0$, then ${\mathrm{\Gamma }}_f$ can be considered as the most general measure of difference between probability measures. For arbitrary convex function f, we notice that ${\mathrm{\Gamma }}_f({\mu }_1,{\mu }_2)\le {\mathrm{\Gamma }}_{|f|}({\mu }_1,{\mu }_2)$.

The Csiszar’s f-divergence ${\mathrm{\Gamma }}_f$ incorporated most of special cases of probability measure distances, including the variation distance, ${\chi }^2$-divergence, information for discrimination or generalized entropy, information gain, mutual information, mean square contingency, etc. ${\mathrm{\Gamma }}_f$ has many applications to almost all applied sciences where stochastics enters. For more references, one can see [12–22].

In this paper, we assume that the base function f appearing in the function ${\mathrm{\Gamma }}_f$ have all the above properties of f.

3 Main results

In the section, we establish some new generalizations of the Hölder inequality involving Csiszar’s f-divergence of two probability measures.

Theorem 3.1 Let $0<a_m<1$, $a_j<0$ ($j=1,2,\dots ,m-1$), $m\in \mathrm{N}$, ${\sum }_{j=1}^m\frac{1}{a_j}=1$. Then

(3.1)

Proof Here, we use the generalized Hölder’s inequality (see [23]). We obtain

(3.2)

Hence, we get the desired inequality. □

Theorem 3.2 Let ${\alpha }_{kj}\in \mathrm{R}$ ($j=1,2,\dots ,m$, $k=1,2,\dots ,s$), ${\sum }_k^s\frac{1}{a_k}=1$, ${\sum }_{k=1}^s{\alpha }_{kj}=0$. Then

• (1) for $a_k>1$, we have the following inequality:

  

  (3.3)

• (2) for $0<a_s<1$, $a_k<0$ ($k=1,2,\dots ,s-1$), we have the following reverse inequality:

  

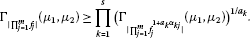  (3.4)

Proof

• (1) Set

  $$g_k(x)={(\prod _{j=1}^m{f}_j^{1+a_k{\alpha }_{kj}}(x))}^{1/a_k}.$$

  (3.5)

Applying the assumptions ${\sum }_k^s\frac{1}{a_k}=1$ and ${\sum }_{k=1}^s{\alpha }_{kj}=0$, we have

$$\begin{array}{rcl}\prod _{k=1}^s{g}_k(x)& =& g_1{g}_2\cdots g_s\\ =& {(\prod _{j=1}^m{f}_j^{1+a_1{\alpha }_{1j}}(x))}^{1/a_1}{(\prod _{j=1}^m{f}_j^{1+a_2{\alpha }_{2j}}(x))}^{1/a_2}\cdots {(\prod _{j=1}^m{f}_j^{1+a_s{\alpha }_{sj}}(x))}^{1/a_s}\\ =& \prod _{j=1}^m{f}_j^{1/a_1+{\alpha }_{1j}}(x)\prod _{j=1}^m{f}_j^{1/a_2+{\alpha }_{2j}}(x)\cdots \prod _{j=1}^m{f}_j^{1/a_s+{\alpha }_{sj}}(x)\\ =& \prod _{j=1}^m{f}_j^{1/a_1+1/a_2+\cdots +1/a_s+{\alpha }_{1j}+{\alpha }_{2j}+\cdots +{\alpha }_{sj}}(x)=\prod _{j=1}^m{f}_j(x).\end{array}$$

That is,

$$\prod _{k=1}^s{g}_k(x)=\prod _{j=1}^m{f}_j(x).$$

Then we find

(3.6)

By the inequality (1.4), we obtain

(3.7)

In view of (3.5), we have

(3.8)

By (3.6), (3.7) and (3.8), we obtain inequality (3.3).

• (2) Similar to the proof of inequality (3.3), by (3.5), (3.6), (3.8) and the inequality (3.1), we have inequality (3.4) immediately. □

Corrollary 3.1 Under the assumptions of Theorem 3.2, taking $s=m$, ${\alpha }_{kj}=-t/a_k$ for $j\ne k$ and ${\alpha }_{kk}=t(1-1/a_k)$ with , then we have

• (1) for ${\alpha }_k>0$, we have the following inequality:

  

  (3.9)

• (2) for $0<{\alpha }_m<1$, ${\alpha }_k<0$ ($k=1,2,\dots ,m-1$), we have the following reverse inequality:

  

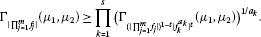  (3.10)

Theorem 3.3 Let ($j=1,2,\dots ,m$, $k=1,2,\dots ,s$), ${\sum }_k^s\frac{1}{{\alpha }_k}=r$, ${\sum }_{k=1}^s{\alpha }_{kj}=0$. Then

• (1) for $r{\alpha }_k>1$, we have the following inequality:

  

  (3.11)

• (2) for $0<r{\alpha }_s<1$, $r{\alpha }_k<0$ ($k=1,2,\dots ,s-1$), we have the following reverse inequality:

  

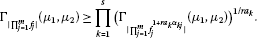  (3.12)

Proof (1) Since $r{\alpha }_k>1$ and ${\sum }_k^s\frac{1}{{\alpha }_k}=r$, we get ${\sum }_k^s\frac{1}{r{\alpha }_k}=1$. Then by (3.3), we immediately obtain the inequality (3.11).

• (2) Since $0<r{\alpha }_s<1$, $r{\alpha }_k<0$ and ${\sum }_k^s\frac{1}{{\alpha }_k}=r$, we have ${\sum }_k^s\frac{1}{r{\alpha }_k}=1$, by (3.4), we immediately have the inequality (3.12). This completes the proof. □

Theorem 3.4 Under the assumptions of Theorem 3.3, and let $s=2$, ${\alpha }_1=p$, ${\alpha }_2=q$, ${\alpha }_{1j}=-{\alpha }_{2j}={\beta }_j$, then

• (1) for $rp>0$, we have the following inequality:

  

  (3.13)

• (2) for $0<rp<1$, we have the following reverse inequality:

  

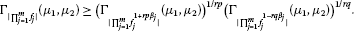  (3.14)

Proof (1) By inequality (1.3), we get

• (2) Similar to the proof of inequality (3.13), by inequality (1.5), we obtain inequality (3.14). □

Remark Assume that X is a finite or countable discrete set, A is its power set $P(X)$ and λ has mass 1 for each $x\in X$, then ${\mathrm{\Gamma }}_f$ becomes a finite or infinite sum, respectively. As a consequence, all the above obtained integral inequalities are discretized and become summation inequalities.