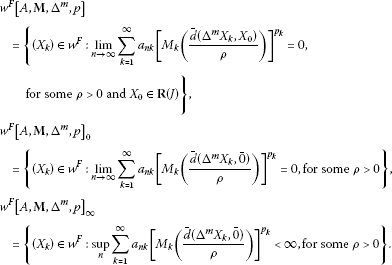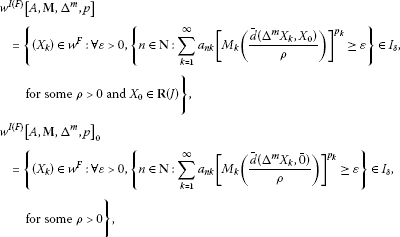- Research
- Open access
- Published:
On some -convergent difference sequence spaces of fuzzy numbers defined by the sequence of Orlicz functions
Journal of Inequalities and Applications volume 2012, Article number: 261 (2012)
Abstract
In this paper, using the difference operator of order m, the sequences of Orlicz functions, and an infinite matrix, we introduce and examine some classes of sequences of fuzzy numbers defined by I-convergence. We study some basic topological and algebraic properties of these spaces. In addition, we shall establish inclusion theorems between these sequence spaces.
MSC:40A05, 40G15, 46A45.
1 Introduction
The notion of ideal convergence was introduced first by Kostyrko et al. [1] as a generalization of statistical convergence [2, 3], which was further studied in topological spaces [4]. More applications of ideals can be seen in [5–9].
The concepts of fuzzy sets and fuzzy set operations were first introduced by Zadeh [10]. Subsequently, several authors have discussed various aspects of the theory and applications of fuzzy sets such as fuzzy topological spaces, similarity relations and fuzzy ordering, fuzzy measures of fuzzy events, and fuzzy mathematical programming. In particular, the concept of fuzzy topology has very important applications in quantum particle physics, especially in connection with both string and theory, which were given and studied by El Naschie [11]. The theory of sequences of fuzzy numbers was first introduced by Matloka [12]. Matloka introduced bounded and convergent sequences of fuzzy numbers, studied some of their properties, and showed that every convergent sequence of fuzzy numbers is bounded. In [13], Nanda studied sequences of fuzzy numbers and showed that the set of all convergent sequences of fuzzy numbers forms a complete metric space. Different classes of sequences of fuzzy real numbers have been discussed by Nuray and Savas [14], Altinok, Colak, and Et [15], Savas [16–20], Savas and Mursaleen [21], and many others.
The study of Orlicz sequence spaces was initiated with a certain specific purpose in Banach space theory. Lindenstrauss and Tzafriri [22] investigated Orlicz sequence spaces in more detail, and they proved that every Orlicz sequence space contains a subspace isomorphic to (). The Orlicz sequence spaces are the special cases of Orlicz spaces studied in [23]. Orlicz spaces find a number of useful applications in the theory of nonlinear integral equations. Although the Orlicz sequence spaces are the generalization of spaces, the -spaces find themselves enveloped in Orlicz spaces [24]. Recently, Savas [19] generalized and for a single sequence of fuzzy numbers by using the Orlicz function and also established some inclusion theorems.
In the later stage, different classes of Orlicz sequence spaces were introduced and studied by Parashar and Choudhary [25], Savas [26–29], and many others.
Throughout the article, denotes the class of all fuzzy real-valued sequence spaces. Also, N and R denote the set of positive integers and the set of real numbers, respectively.
The operator is defined by ; ; () for all . The generalized difference has the following binomial expression for :
In this paper, we study some new sequence spaces of fuzzy numbers using I-convergence, the sequence of Orlicz functions, an infinite matrix, and the difference operator. We establish the inclusion relation between the sequence spaces , , , and , where denotes the sequence of positive real numbers for all and is a sequence of Orlicz functions. In addition, we study some algebraic and topological properties of these new spaces.
2 Definitions and notations
Before continuing with this paper, we present some definitions and preliminaries which we shall use throughout this paper.
Let X and Y be two nonempty subsets of the space w of complex sequences. Let () be an infinite matrix of complex numbers. We write if converges for each n. (Throughout, denotes summation over k from to ). If , we say that A defines a (matrix) transformation from X to Y and we denote it by .
Let X be a nonempty set, then a family of sets (the class of all subsets of X) is called an ideal if and only if for each , we have , and for each and each , we have . A nonempty family of sets is a filter on X if and only if , for each , we have , and for each and each , we have . An ideal I is called non-trivial ideal if and . Clearly, is a non-trivial ideal if and only if is a filter on X. A non-trivial ideal is called admissible if and only if . A non-trivial ideal I is maximal if there cannot exist any non-trivial ideal containing I as a subset. Further details on ideals of can be found in Kostyrko et al. [1].
Let D denote the set of all closed and bounded intervals on the real line R. For , we define if and only if and ,
Then it can be easily seen that d defines a metric on D and is a complete metric space (see [30]). Also, the relation ‘≤’ is a partial order on D. A fuzzy number X is a fuzzy subset of the real line R, i.e., a mapping () associating each real number t with its grade of membership . A fuzzy number X is convex if , where . If there exists such that , then the fuzzy number X is called normal. A fuzzy number X is said to be upper semicontinuous if for each , for all is open in the usual topology in R. Let denote the set of all fuzzy numbers which are upper semicontinuous and have compact support, i.e., if , then for any , is compact, where

The set R of real numbers can be embedded in if we define by
The additive identity and multiplicative identity of are defined by and respectively.
The arithmetic operations on are defined as follows:

Let and the α-level sets be , , . Then the above operations can be defined in terms of α-level sets as follows:

For and , the product rX is defined as follows:
The absolute value of is defined by
Define a mapping by
A metric on is said to be a translation invariant if for .
Proposition 2.1 If is a translation invariant metric on , then
-
(i)
,
-
(ii)
, .
The proof is easy and so it is omitted.
A sequence of fuzzy numbers is said to converge to a fuzzy number if for every , there exists a positive integer such that for all .
A sequence of fuzzy numbers is said to be bounded if the set of fuzzy numbers is bounded. A sequence of fuzzy numbers is said to be I-convergent to a fuzzy number if for each such that
The fuzzy number is called I-limit of the sequence of fuzzy numbers, and we write .
A sequence of fuzzy numbers is said to be I-bounded if there exists such that
Example 2.1 If we take , then is a non-trivial admissible ideal of N, and the corresponding convergence coincides with the usual convergence.
Example 2.2 If we take , where denotes the asymptotic density of the set A, then is a non-trivial admissible ideal of N, and the corresponding convergence coincides with the statistical convergence.
Lemma 2.1 (Kostyrko, Salat, and Wilczynski [1], Lemma 5.1)
If is a maximal ideal, then for each , we have either or .
Recall in [23] that the Orlicz function is a continuous, convex, non-decreasing function such that and for , and as . If convexity of the Orlicz function is replaced by , then this function is called the modulus function and characterized by Ruckle [31]. An Orlicz function M is said to satisfy the -condition for all values of u, if there exists such that , .
The following well-known inequality will be used throughout the article. Let be any sequence of positive real numbers with , , then
for all and . Also, for all .
3 Some new sequence spaces of fuzzy numbers
In this section, using the sequence of Orlicz functions, an infinite matrix, the difference operator , and I-convergence, we introduce the following new sequence spaces and examine some properties of the resulting sequence spaces. Let I be an admissible ideal of N, and let be a sequence of positive real numbers for all and be an infinite matrix. Let be a sequence of Orlicz functions and be a sequence of fuzzy numbers. We define the following new sequence spaces:

and

Let us consider a few special cases of the above sets.
-
(i)
If , then the above classes of sequences are denoted by , , , and , respectively.
-
(ii)
If for all , then the above classes of sequences are denoted by , , , and , respectively.
-
(iii)
If , then we denote the above spaces by , , , and .
-
(iv)
If we take , i.e., the Cesàro matrix, then the above classes of sequences are denoted by , , , and , respectively.
-
(v)
If we take is a de la Valée Poussin mean, i.e.,
where is a non-decreasing sequence of positive numbers tending to ∞ and , , then the above classes of sequences are denoted by , , , and , respectively (see [32]).
-
(vi)
By a lacunary , where , we shall mean an increasing sequence of non-negative integers with as . The intervals determined by θ will be denoted by and . As a final illustration, let
Then we denote the above classes of sequences by , , , and , respectively.
-
(vii)
If , then we obtain
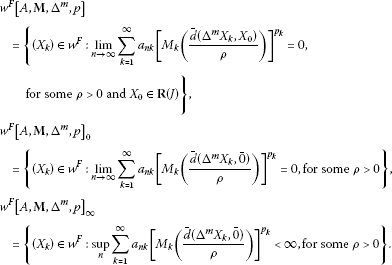
If , then we say that is strongly A-convergent with respect to the sequence of Orlicz functions M.
-
(viii)
If is an admissible ideal of N, then we obtain
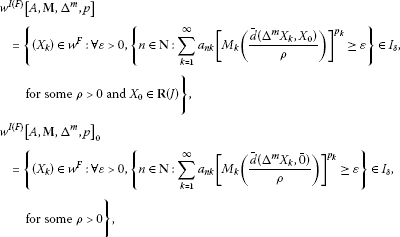
and

4 Main results
In this section, we examine the basic topological and algebraic properties of the new sequence spaces and obtain the inclusion relation related to these spaces.
Theorem 4.1 Let be a bounded sequence. Then the sequence spaces , , and are linear spaces.
Proof We will prove the result for the space only and others can be proved in a similar way.
Let and be two elements in . Then there exist and such that
and
Let α, β be two scalars. By the continuity of the function , the following inequality holds:

where .
From the above relation, we obtain the following:

This completes the proof. □
Theorem 4.2 , , and are linear topological spaces with the paranorm defined by
where .
Proof Clearly, and . Let and be two elements in . Then for every , we write
and
Let and . If , then we get the following:
Hence, we obtain
and
□
Let , where , , and let as . To prove that as , let , where and as .
We have
and
If and and by continuity of the function , we have that

From the above inequality, it follows that
and consequently
Note that for all .
Hence, by our assumption, the right-hand side tends to 0 as . This completes the proof of the theorem.
Theorem 4.3 Let I be an admissible ideal and be a sequence of Orlicz functions. Then the following hold:
; ; for and the inclusions are strict.
In general, for all , the following hold:
; ; and the inclusions are strict.
Proof Let be an element in . Then there exists , and for given , , we have
Since is non-decreasing and convex, it follows that

Hence, we have

□
The inclusion is strict, it follows from the following example.
Example 4.1 Let , for all and , i.e., the Cesàro matrix, . Consider the sequence of fuzzy numbers as follows:
For , α-level sets of , , , and are

respectively. It is easy to see that the sequence is not I-bounded although is I-bounded.
Theorem 4.4 (a) Let . Then
; .
(b) Let . Then
; .
Proof (a) Let be an element in . Since , we have
Therefore,

The other part can be proved in a similar way.
-
(b)
Let be an element in . Since , then for each , there exists a positive integer such that
This implies that
Therefore, we have

□
The other part can be proved in a similar way.
The following corollary follows immediately from the above theorem.
Corollary 4.5 Let , i.e., the Cesàro matrix, and be a sequence of Orlicz functions.
(a) Let . Then
; .
(b) Let . Then
; .
References
Kostyrko P, Salat T, Wilczyński W: I -Convergence. Real Anal. Exch. 2000, 26(2):669–686.
Fast H: Sur la convergence statistique. Colloq. Math. 1951, 2: 241–244.
Steinhaus H: Sur la convergence ordinarie et la convergence asymptotique. Colloq. Math. 1951, 2: 73–74.
Pratulananda D, Lahiri BK: I and convergence in topological spaces. Math. Bohem. 2005, 130(2):153–160.
Pratulananda D, Kostyrko P, Wilczyński W, Malik P: I and -convergence of double sequences. Math. Slovaca 2008, 58: 605–620. 10.2478/s12175-008-0096-x
Savas E, Pratulananda D: A generalized statistical convergence via ideals. Appl. Math. Lett. 2011. doi:10.1016/j.aml.2010.12.022
Savas E:-strongly summable sequences spaces in 2-normed spaces defined by ideal convergence and an Orlicz function. Appl. Math. Comput. 2010, 217: 271–276. 10.1016/j.amc.2010.05.057
Savas E: A-sequence spaces in 2-normed space defined by ideal convergence and an Orlicz function. Abstr. Appl. Anal. 2011., 2011: Article ID 741382
Savas E: On some new sequence spaces in 2-normed spaces using Ideal convergence and an Orlicz function. J. Inequal. Appl. 2010., 2010: Article ID 482392. doi:10.1155/2010/482392
Zadeh LA: Fuzzy sets. Inf. Control 1965, 8: 338–353. 10.1016/S0019-9958(65)90241-X
El Naschie MS:A review of , theory and the mass spectrum of high energy particle physics. Chaos Solitons Fractals 2004, 19(1):209–236. 10.1016/S0960-0779(03)00278-9
Matloka M: Sequences of fuzzy numbers. BUSEFAL 1986, 28: 28–37.
Nanda S: On sequences of fuzzy numbers. Fuzzy Sets Syst. 1989, 33: 123–126. 10.1016/0165-0114(89)90222-4
Nuray F, Savas S: Statistical convergence of sequences of fuzzy numbers. Math. Slovaca 1995, 45: 269–273.
Altinok H, Colak R, Et M: λ -Difference sequence spaces of fuzzy numbers. Fuzzy Sets Syst. 2009, 160: 3128–3139. 10.1016/j.fss.2009.06.002
Savaş E: A note on sequence of fuzzy numbers. Inf. Sci. 2000, 124: 297–300. 10.1016/S0020-0255(99)00073-0
Savaş E: On strongly λ -summable sequences of fuzzy numbers. Inf. Sci. 2000, 125: 181–186. 10.1016/S0020-0255(99)00151-6
Savaş E: On statistically convergent sequence of fuzzy numbers. Inf. Sci. 2001, 137: 272–282.
Savaş E: Difference sequence spaces of fuzzy numbers. J. Fuzzy Math. 2006, 14(4):967–975.
Savaş E: On lacunary statistical convergent double sequences of fuzzy numbers. Appl. Math. Lett. 2008, 21: 134–141. 10.1016/j.aml.2007.01.008
Savaş E, Mursaleen M: On statistically convergent double sequence of fuzzy numbers. Inf. Sci. 2004, 162: 183–192. 10.1016/j.ins.2003.09.005
Lindenstrauss J, Tzafriri L: On Orlicz sequence spaces. Isr. J. Math. 1971, 101: 379–390.
Krasnoselskii MA, Rutitsky YB: Convex Functions and Orlicz Functions. Noordhoff, Groningen; 1961.
Kamthan PK, Gupta M: Sequence Spaces and Series. Marcel Dekker, New York; 1980.
Parashar SD, Choudhury B: Sequence space defined by Orlicz functions. Indian J. Pure Appl. Math. 1994, 25(14):419–428.
Savaş E, Patterson RF: An Orlicz extension of some new sequence spaces. Rend. Ist. Mat. Univ. Trieste 2005, 37(1–2):145–154. (2006)
Savaş E, Savas R: Some sequence spaces defined by Orlicz functions. Arch. Math. 2004, 40(1):33–40.
Savas E, Patterson RF: Some double lacunary sequence spaces defined by Orlicz functions. Southeast Asian Bull. Math. 2011, 35(1):103–110.
Savas E: On some new double lacunary sequences spaces via Orlicz function. J. Comput. Anal. Appl. 2009, 11(3):423–430.
Kaleva O, Seikkala S: On fuzzy metric spaces. Fuzzy Sets Syst. 1984, 12: 215–229. 10.1016/0165-0114(84)90069-1
Ruckle WH: FK-spaces in which the sequence of coordinate vectors is bounded. Can. J. Math. 1973, 25: 973–978. 10.4153/CJM-1973-102-9
Hazarika B, Savaş E: Some I -convergent lamda-summable difference sequence spaces of fuzzy real numbers defined by a sequence of Orlicz. Math. Comput. Model. 2011, 54: 2986–2998. 10.1016/j.mcm.2011.07.026
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Savas, E. On some -convergent difference sequence spaces of fuzzy numbers defined by the sequence of Orlicz functions. J Inequal Appl 2012, 261 (2012). https://doi.org/10.1186/1029-242X-2012-261
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-261