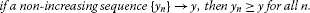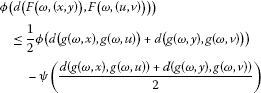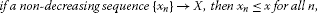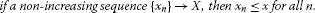- Research
- Open access
- Published:
Weak contractive inequalities and compatible mixed monotone random operators in ordered metric spaces
Journal of Inequalities and Applications volume 2012, Article number: 257 (2012)
Abstract
The aim of this work is to define the notion of compatible random operators in a partially ordered metric space and prove some coupled random coincidence theorems for a pair of compatible mixed monotone random operators satisfying -weak contractive conditions. These results present random versions and extensions of recent results of Ćirić and Lakshmikantham (Stoch. Anal. Appl. 27:1246-1259, 2009), Choudhury and Kundu (Nonlinear Anal. 73:2524-2531, 2010), Alotaibi and Alsulami (Fixed Point Theory Appl. 2011:44, 2011) and many others.
1 Introduction
Random coincidence point theorems are stochastic generalizations of classical coincidence point theorems. Some random fixed point theorems play an important role in the theory of random differential and random integral equations (see [1, 2]). Random fixed point theorems for contractive mappings on separable complete metric spaces have been proved by several authors [3–8]. Sehgal and Singh [9] have proved different stochastic versions of the well-known Schauder fixed point theorem. Fixed point theorems for monotone operators in ordered Banach spaces have been investigated and have found various applications in differential and integral equations (see [10–12] and references therein). Fixed point theorems for mixed monotone mappings in partially ordered metric spaces are of great importance and have been utilized for matrix equations, ordinary differential equations, and for the existence and uniqueness of solutions for some boundary value problems (see [13–19]).
Recently Ćirić and Lakshmikantham [20] and Zhu and Xiao [21] proved some coupled random fixed point and coupled random coincidence results in partially ordered complete metric spaces. The purpose of this article is to improve these results for a pair of compatible mixed monotone random mappings and , where F and g satisfy the -weak contractive conditions. Presented results are also the extensions and improvements of the corresponding results in [22–24] and many others.
2 Preliminaries
Recall that if is a partially ordered set and is such that for , implies , then a mapping F is said to be non-decreasing. Similarly, a non-increasing map may be defined. Bhaskar and Lakshmikantham [25] introduced the following notions of a mixed monotone mapping and a coupled fixed point.
Definition 2.1 ([25])
Let be a partially ordered set and . The mapping F is said to have the mixed monotone property if F is monotone non-decreasing in its first argument and is monotone non-increasing in its second argument, that is, for any ,
and
Definition 2.2 ([25])
An element is called a coupled fixed point of the mapping if
The concept of the mixed monotone property is generalized in [24].
Definition 2.3 ([24])
Let be a partially ordered set and and . The mapping F is said to have the mixed g-monotone property if F is monotone g-non-decreasing in its first argument and is monotone g-non-increasing in its second argument, that is, for any ,
and
Definition 2.4 An element is called a coupled fixed point of the mapping and if
Definition 2.5 The mappings F and g, where and , are said to be compatible if
and
whenever , are sequences in X such that and for all are satisfied.
Using the concept of compatible maps and the mixed g-monotone property, Choudhury and Kundu [23] proved the following theorem.
Theorem 2.6 Let be a partially ordered set, and let there be a metric d on X such that is a complete metric space. Let be such that and for all . Let and be two mappings such that F has the mixed g-monotone property and satisfy
for all , for which and . Let , g be continuous and monotone increasing and F and g be compatible mappings. Also, suppose either
-
(a)
F is continuous or
-
(b)
X has the following properties:
-
(i)
if a non-decreasing sequence , then for all ,
-
(ii)
if a non-increasing sequence , then for all .
If there exist , such that and , then there exist such that and , that is, F and g have a coupled coincidence point in X.
As in [17], let Φ denote all functions which satisfy
-
1.
ϕ is continuous and non-decreasing,
-
2.
if and only if ,
-
3.
, ,
and let Ψ denote all the functions which satisfy for all and .
Alotaibi and Alsulami in [22] proved the following coupled coincidence result for monotone operators in partially ordered metric spaces.
Theorem 2.7 Let be a partially ordered set and suppose there is a metric d on X such that is a complete metric space. Let be a mapping having the mixed g-monotone property on X such that there exist two elements with
Suppose there exist and such that
for all with and . Suppose , g is continuous and compatible with F and also suppose either
-
(a)
F is continuous or
-
(b)
X has the following property:
-
(i)
if a non-decreasing sequence , then for all n,
-
(ii)
if a non-increasing sequence , then for all n.
Then there exists such that
that is, F and g have a coupled coincidence point in X.
3 Main results
Let be a measurable space with Σ being a sigma algebra of subsets of Ω, and let be a metric space. A mapping is called Σ-measurable if for any open subset U of X, . In what follows, when we speak of measurability, we will mean Σ-measurability. A mapping is called a random operator if for any , is measurable. A measurable mapping is called a random fixed point of a random function if for every . A measurable mapping is called a random coincidence of and if for every .
Definition 3.1 Let be a separable metric space and be a measurable space. Then and are said to be compatible random operators if
and
whenever , are sequences in X, such that and for all and are satisfied.
As in [23], let be such that and for all .
Now, we state our main result.
Theorem 3.2 Let be a complete separable partially ordered metric space, be a measurable space, and and be mappings such that
-
(i)
is continuous for all ;
-
(ii)
, are measurable for all and respectively;
-
(iii)
has the mixed -monotone property for each and
(1)
for all , for which and for all .
Suppose for each , g is monotone increasing, and F and g are compatible random operators. Also suppose either
-
(a)
is continuous for all or
-
(b)
X has the following property:
 (2)
(2)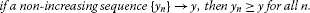 (3)
(3)
If there exist measurable mappings such that and for all , then there are measurable mappings such that and for all , that is, F and g have a coupled random coincidence point.
Proof Let be a family of measurable mappings. Define a function as follows:
Since is continuous for all , we conclude that is continuous for all . Also, since is measurable for all , we conclude that is measurable for all (see [26], p.868). Thus, is the Caratheodory function. Therefore, if is a measurable mapping, then is also measurable (see [27]). Also, for each , the function defined by is measurable, that is, .
Now, we shall construct two sequences of measurable mappings and in Θ, and two sequences and in X as follows. Let be such that and for all . Since by an appropriate Filippov measurable implicit function theorem [1, 20, 28, 29], there is such that . Similarly, as , there is such that . Now and are well defined. Again from , there are such that and . Continuing this process, we can construct sequences and in X such that
for all .
We shall prove that
and
The proof will be given by mathematical induction. Let . By assumption we have and . Since and , we have
Therefore, (5) and (6) hold for .
Suppose now that (5) and (6) hold for some fixed . Then, since and and as F is monotone g-non-decreasing in its first argument, from (2) and (4), we have
Similarly, from (3) and (4), as and ,
Now from (7), (8), and (4), we get
and
Thus, by mathematical induction we conclude that (5) and (6) hold for all .
Denote for each
We show that
Since from (5) and (6) we have and , therefore from (4) and (1), we get

Similarly, from (4) and (1), as and ,

By adding (12) and (13), and dividing by 2, we obtain (11).
From (11), since for , it follows that is the monotone decreasing sequence of positive reals. Therefore, there is some such that
We show that . Suppose, to the contrary, that . Taking the limit in (11) when and having in mind that we assume that for all , we have
a contradiction. Thus, .
Now we prove that for each , and are Cauchy sequences. Suppose, to the contrary, that at least one, or , is not a Cauchy sequence. Then there exist an and two subsequences of positive integers , , with
for .
We may also assume
By choosing to be the smallest number exceeding for which (14) holds, such for which (15) holds exists, because . From (14), (15) and by the triangle inequality, we have
Taking the limit as , we get
Inequality (14) and the triangle inequality imply now
Hence,
From (5) and (6), we conclude that and .
Now (1) and (4) imply that

Also, from (1) and (4), as and ,

Inserting (18) and (19) in (17), we obtain
Letting , we get by (16)
a contradiction. Therefore, our supposition (14) was wrong. Thus, we proved that and are Cauchy sequences in X.
Since X is complete and , there exist such that and . Since and are measurable, therefore the functions and , defined by and are measurable. Thus,
Since F and g are compatible mappings, we have by (21)


Next, we prove that
and
Let (a) hold. We have

Taking the limit as , using (4), (21), and (22) and the fact that F and g are continuous, we have
Similarly, from (4), (21), and (23) and the continuity of F and g, we have
Combining the above two results, we obtain
and
for each .
Next, suppose that (b) holds. From (5), (6), and (21), we have is non-decreasing and is non-increasing sequence and
So, from (2) and (3), we have for all
Since F and g are compatible mappings and g is continuous, by (22) and (23) we have

and

Now, we have

Taking the limit as in the above inequality, using (4) and (25), we have

Since the mapping g is monotone increasing, by (1), (24), and the above inequality, we have for all

Using (21) and the property of a φ-function, we obtain
That is,
And similarly, by the virtue of (4), (21), and (26), we obtain
This proves that F and g have a coupled random coincidence point. □
Corollary 3.3 Let be a complete separable partially ordered metric space, be a measurable space, and and be mappings such that
-
(i)
is continuous for all ;
-
(ii)
, are measurable for all and respectively;
-
(iii)
has the mixed -monotone property for each and for some
for all , for which and for all .
Suppose for each , g is monotone increasing, and F and g are compatible random operators. Also suppose either
-
(a)
is continuous for all or
-
(b)
X has the following property:
-
(i)
if a non-decreasing sequence , then for all n,
-
(ii)
if a non-increasing sequence , then for all n.
If there exist measurable mappings such that and for all , then there are measurable mappings such that and for all , that is, F and g have a coupled random coincidence point.
Proof Taking with in Theorem 3.2, we obtain the result. □
The following theorem presents the stochastic version of Theorem 2.7 and generalizes the recent results in [20].
Theorem 3.4 Let be a complete separable partially ordered metric space, be a measurable space, and and be mappings such that
-
(i)
is continuous for all ;
-
(ii)
, are measurable for all and , respectively;
-
(iii)
and are such that has the mixed -monotone property for each ; and suppose there exist and , satisfying conditions of Theorem 2.7, such that
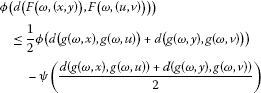 (27)
(27)
for all , for which and for all .
Suppose for each , g is monotone increasing, and F and g are compatible random operators. Also suppose either
-
(a)
is continuous for all or
-
(b)
X has the following property:
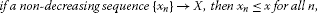 (28)
(28)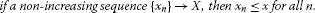 (29)
(29)
If there exist measurable mappings such that and for all , then there are measurable mappings such that and for all , that is, F and g have a coupled random coincidence.
Proof Let be a family of measurable mappings. Define a function as follows:
Since is continuous for all , we conclude that is continuous for all . Also, since is measurable for all , we conclude that is measurable for all (see [26], p.868). Thus, is the Caratheodory function. Therefore, if is a measurable mapping, then is also measurable (see [27]). Also, for each , the function defined by is measurable, that is, . Now, we shall construct two sequences of measurable mappings and in ⊖, and two sequences and in X as follows. Let such that and for all . Since , by an appropriate Filippov measurable implicit function theorem [1, 20, 28, 29], there is such that . Similarly, as , there is such that . Now, and are well defined. Again, from , there are such that and . Continuing this process, we can construct sequences and in X such that
for all .
We shall prove that
and
The proof will be given by mathematical induction. Let . By assumption, we have and . Since and , we have and . Therefore, (31) and (32) hold for . Suppose now that (31) and (32) hold for some fixed . Then and as F is monotone g-non-decreasing in its first argument, from (28) and (30),
Similarly, from (29) and (30), as and , we have
Now, from (30), (33), and (34), we get
and
Thus, by mathematical induction we conclude that (31) and (32) hold for all .
Therefore,
and
Since and , using (27) and (30), we have

Similarly, since and , using (27) and (30), we also have

Using (39) and (40), we have

From the property (iii) of ϕ, we have

Using (41) and (42), we have

Since ψ is a non-negative function, therefore we have

Using the fact that ϕ is non-decreasing, we get

Let
Now, we show that as . It is clear that the sequence is decreasing; therefore, there is some such that
We shall show that . Suppose, to the contrary, that . Then taking the limit as on both sides of (43) and as for all and ϕ is continuous, we have
a contradiction. Thus, , that is
Now, we will prove that , are Cauchy sequences. Suppose, to the contrary, that at least one of or is not a Cauchy sequence. Then there exists an for which we can find subsequences of positive integers , with such that
for . We may also assume
by choosing in such a way that it is the smallest integer with and satisfying (46). Using (46), (47), and the triangle inequality, we have
Letting and using (45), we get
By the triangle inequality,

Using the property of ϕ, we have
Since , hence and . Using (27) and (30), we get

By the same way, we also have

Putting (50) and (51) in (49), we have
Taking and using (45) and (48), we get
a contradiction. This shows that and are Cauchy sequences.
Since X is complete and , there exist such that and . Since and are measurable, then the functions and , defined by and , are measurable. Thus,
Using the compatibility of F and g and the technique of the proof of Theorem 3.2, we obtain the required conclusion. □
Corollary 3.5 Let be a complete separable partially ordered metric space, be a measurable space, and and be mappings such that
-
(i)
is continuous for all ;
-
(ii)
, are measurable for all and respectively;
-
(iii)
has the mixed -monotone property for each ; and suppose there exist and such that
for all , for which and for all .
Suppose for each , g is continuous and monotone increasing, and F and g are compatible mappings. Also suppose either
-
(a)
is continuous for all or
-
(b)
X has the following property:
-
(i)
if a non-decreasing sequence , then for all n,
-
(ii)
if a non-increasing sequence , then for all n.
If there exist measurable mappings such that and for all , then there are measurable mappings such that and for all , that is, F and g have a coupled random coincidence.
Proof Take in Theorem 3.4. □
Corollary 3.6 Let be a complete separable partially ordered metric space, be a measurable space, and and be mappings such that
-
(i)
is continuous for all ;
-
(ii)
, are measurable for all and respectively;
-
(iii)
has the mixed -monotone property for each ; and suppose there exists such that
for all , for which and for all .
Suppose for each , g is monotone increasing, and F and g are compatible random operators. Also suppose either
-
(a)
is continuous for all or
-
(b)
X has the following property:
-
(i)
if a non-decreasing sequence , then for all n,
-
(ii)
if a non-increasing sequence , then for all n.
If there exist measurable mappings such that and for all , then there are measurable mappings such that and for all , that is, F and g have a coupled random coincidence point.
Proof Take in Corollary 3.5. □
Remark 3.7 By defining as for all in Theorem 3.2-Corollary 3.6, we obtain corresponding coupled random fixed point results.
References
Itoh S: A random fixed point theorem for a multi-valued contraction mapping. Pac. J. Math. 1977, 68: 85–90. 10.2140/pjm.1977.68.85
Lin TC: Random approximations and random fixed point theorems for non-self maps. Proc. Am. Math. Soc. 1988, 103: 1129–1135. 10.1090/S0002-9939-1988-0954994-0
Abbas M, Hussain N, Rhoades BE: Coincidence point theorems for multivalued f -weak contraction mappings and applications. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A, Mat. 2011, 105: 261–272.
Agarwal RP, O’Regan D, Sambandham M: Random and deterministic fixed point theory for generalized contractive maps. Appl. Anal. 2004, 83: 711–725. 10.1080/00036810410001657206
Beg I, Khan AR, Hussain N: Approximation of ∗-nonexpansive random multivalued operators on Banach spaces. J. Aust. Math. Soc. 2004, 76: 51–66. 10.1017/S1446788700008697
Ćirić LB, Ješić SN, Ume JS: On random coincidence for a pair of measurable mappings. J. Inequal. Appl. 2006., 2006: Article ID 81045
Huang NJ: A principle of randomization of coincidence points with applications. Appl. Math. Lett. 1999, 12: 107–113.
Khan AR, Hussain N: Random coincidence point theorem in Frechet spaces with applications. Stoch. Anal. Appl. 2004, 22: 155–167.
Sehgal VM, Singh SP: On random approximations and a random fixed point theorem for set valued mappings. Proc. Am. Math. Soc. 1985, 95: 91–94. 10.1090/S0002-9939-1985-0796453-1
Agarwal RP, Hussain N, Taoudi MA: Fixed point theorems in ordered Banach spaces and applications to nonlinear integral equations. Abstr. Appl. Anal. 2012., 2012: Article ID 245872
Chen Y-Z: Fixed points for discontinuous monotone operators. J. Math. Anal. Appl. 2004, 291: 282–291. 10.1016/j.jmaa.2003.11.003
Hussain N, Khan AR, Agarwal RP: Krasnosel’skii and Ky Fan type fixed point theorems in ordered Banach spaces. J. Nonlinear Convex Anal. 2010, 11(3):475–489.
Agarwal RP, El-Gebeily MA, O’Regan D: Generalized contractions in partially ordered metric spaces. Appl. Anal. 2008, 87: 109–116. 10.1080/00036810701556151
Hussain N, Alotaibi A: Coupled coincidences for multi-valued nonlinear contractions in partially ordered metric spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 82. doi:10.1186/1687–1812–2011–82
Hussain N, Latif A, Shah MH: Coupled and tripled coincidence point results without compatibility. Fixed Point Theory Appl. 2012., 2012: Article ID 77
Lakshimkantham V, Vatsala AS: General uniqueness and monotone iterative technique for fractional differential equations. Appl. Math. Lett. 2008, 21: 828–834. 10.1016/j.aml.2007.09.006
Luong NV, Thuan NX: Coupled fixed point in partially ordered metric spaces and applications. Nonlinear Anal. 2011, 74: 983–992. 10.1016/j.na.2010.09.055
Nieto JJ, Rodriguez-Lopez R: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005, 22: 223–239. 10.1007/s11083-005-9018-5
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proc. Am. Math. Soc. 2004, 132: 1435–1443. 10.1090/S0002-9939-03-07220-4
Ćirić LB, Lakshmikantham V: Coupled random fixed point theorems for nonlinear contractions in partially ordered metric spaces. Stoch. Anal. Appl. 2009, 27: 1246–1259. 10.1080/07362990903259967
Zhu X-H, Xiao J-Z: Random periodic point and fixed point results for random monotone mappings in ordered Polish spaces. Fixed Point Theory Appl. 2010., 2010: Article ID 723216
Alotaibi A, Alsulami S: Coupled coincidence points for monotone operators in partially ordered metric spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 44
Choudhury BS, Kundu A: A coupled coincidence point in partially ordered metric spaces for compatible mappings. Nonlinear Anal. 2010, 73: 2524–2531. 10.1016/j.na.2010.06.025
Lakshimkantham V, Ćirić LB: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal. 2009, 70: 4341–4349. 10.1016/j.na.2008.09.020
Bhaskar TG, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. 2006, 65: 1379–1393. 10.1016/j.na.2005.10.017
Wagner DH: Survey of measurable selection theorems. SIAM J. Control Optim. 1977, 15: 859–903. 10.1137/0315056
Rockafellar RT: Measurable dependence of convex sets and functions in parameters. J. Math. Anal. Appl. 1969, 28: 4–25. 10.1016/0022-247X(69)90104-8
Himmelberg CJ: Measurable relations. Fundam. Math. 1975, 87: 53–72.
McShane EJ, Warified RB Jr.: On Filippov’s implicit functions lemma. Proc. Am. Math. Soc. 1967, 18: 41–47.
Acknowledgements
The first and second author gratefully acknowledge the support from the Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU) during this research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hussain, N., Latif, A. & Shafqat, N. Weak contractive inequalities and compatible mixed monotone random operators in ordered metric spaces. J Inequal Appl 2012, 257 (2012). https://doi.org/10.1186/1029-242X-2012-257
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-257