- Research
- Open access
- Published:
Solvability and iterative algorithms for a system of generalized nonlinear mixed quasivariational inclusions with -monotone operators
Journal of Inequalities and Applications volume 2012, Article number: 235 (2012)
Abstract
In this paper, we introduce and discuss a new system of generalized nonlinear mixed quasivariational inclusions with -monotone operators in Hilbert spaces, which includes several systems of variational inequalities and variational inclusions as special cases. By employing the resolvent operator technique associated with -monotone operators, we suggest two iterative algorithms for computing the approximate solutions of the system of generalized nonlinear mixed quasivariational inclusions. Under certain conditions, we obtain the existence of solutions for the system of generalized nonlinear mixed quasivariational inclusions and prove the convergence of the iterative sequences generated by the iterative algorithms. The results presented in this paper extend, improve and unify many known results in recent literature.
MSC:47J20, 49J40.
1 Introduction
Variational inclusions, as important extensions of the classical variational inequalities, provide us with simple, natural, general and unified frameworks in the study of many fields including mechanics, physics, optimization and control, nonlinear programming, economics and transportation equilibrium, as well as engineering sciences. Owing to their wide applications, a lot of existence results and iterative algorithms of solutions for various variational inclusions have been studied in recent years. For details, we refer to [1–20] and the references therein. Among these methods, the resolvent operator techniques to solve various variational inclusions are interesting and important.
In the past years, Agarwal-Huang-Tan [1] introduced a system of generalized nonlinear mixed quasivariational inclusions and investigated the sensitivity analysis of solutions for the system of generalized nonlinear mixed quasivariational inclusions in Hilbert spaces. Kazmi-Bhat [8] introduced a system of nonlinear variational-like inclusions and gave an iterative algorithm for finding its approximate solution. Fang-Huang [4], Huang-Fang [6] and Liu-Kang-Ume [13] introduced some new systems of variational inclusions in Hilbert spaces using the resolvent operator associated with H-monotone operators, maximal η-monotone operators, maximal monotone operators and A-monotone operators, respectively. Afterward, Fang-Huang-Thompson [5] studied a class of variational inclusions with -monotone operators, which provides a unifying framework for the classes of maximal monotone operators, maximal η-monotone operators and H-monotone operators. Jin-Liu-Lee [7] studied a class of generalized nonlinear mixed quasivariational inclusions including relaxed Lipschitz and relaxed monotone operators.
Motivated and inspired by the above works, the goal of this paper is as follows. First, a new system of generalized nonlinear mixed quasivariational inclusions with -monotone operators is introduced and studied in Hilbert spaces. Secondly, by utilizing some properties of the resolvent operators with -monotone operators, two new iterative algorithms for approximating solutions of the system of generalized nonlinear mixed quasivariational inclusions are constructed. Finally, we prove the existence of solutions for the system of generalized nonlinear mixed quasivariational inclusions and show the convergence of the iterative sequences generated by the iterative algorithms in Hilbert spaces. Our results generalize, improve and unify a lot of previously known results in this area.
2 Preliminaries
In this paper, we assume that ℋ is a real Hilbert space whose norm and inner product are denoted by and , respectively. Let denote the family of all nonempty closed bounded subsets of ℋ and denote the Hausdorff metric on defined by
where , . Set  , ω and
, ω and  denote the sets of all nonnegative and positive integers, respectively.
denote the sets of all nonnegative and positive integers, respectively.
In what follows, we recall some basic concepts, assumptions and results, which will be used in the sequel.
Definition 2.1 Let , be two operators and be a set-valued operator. M is said to be
-
(1)
η-monotone if , , , ;
-
(2)
-monotone if M is η-monotone and for all .
Remark 2.1 The class of -monotone operators is much more universal than all maximal η-monotone, maximal monotone, H-monotone and η-monotone operators.
Definition 2.2 An operator is said to be Lipschitz continuous if there exists a constant such that
Definition 2.3 Let , be operators. The operator g is said to be
-
(1)
Lipschitz continuous if there exists a constant such that
-
(2)
strongly monotone if there exists a constant satisfying
-
(3)
η-monotone if , ;
-
(4)
strictly η-monotone if g is η-monotone and if and only if ;
-
(5)
strongly η-monotone if there exists a constant fulfilling
-
(6)
m-relaxed monotone if there exists a constant such that
Definition 2.4 A set-valued operator is said to be -Lipschitz continuous if there exists a constant such that
Definition 2.5 ([5])
Let be an operator, be a strictly η-monotone operator and be an -monotone operator. Then the resolvent operator is defined by
Lemma 2.1 ([5])
Let be a Lipschitz continuous operator with a constant , be a strongly η-monotone operator with a constant and be an -monotone operator. Then the resolvent operator is Lipschitz continuous with a constant , that is,
Lemma 2.2 ([21])
Let , , be three nonnegative real sequences satisfying
where , , and . Then .
Lemma 2.3 ([22])
Let be a metric space and be a set-valued mapping. Then for any given and any given , , there exists such that
where H is the Hausdorff metric on .
In what follows, unless specified otherwise, we always assume that for each , is a real Hilbert space with norm , inner product and Hausdorff metric .
Definition 2.6 Let , be two operators. The operator F is said to be
-
(1)
Lipschitz continuous in the first argument if there exists a constant such that
-
(2)
H-relaxed monotone in the first argument if there exists a constant satisfying
In a similar way, we can define the corresponding concepts for the operator F in the second argument.
3 A system of generalized nonlinear mixed quasivariational inclusions and iterative algorithms
In this section, we shall introduce a new system of generalized nonlinear mixed quasivariational inclusions including -monotone operators in Hilbert spaces, and construct a new iterative algorithm for solving the system of generalized nonlinear mixed quasivariational inclusions. Furthermore, a more general and unified iterative algorithm called the Mann perturbed iterative algorithm with mixed errors is constructed as well in Hilbert spaces.
For each , let , be operators, be set-valued operator such that for each fixed , is -monotone and is -monotone, , be operators and , be four set-valued operators. Let ρ and ν be two positive constants. For any , we consider the following problem:
Find such that , , , , , , and
where , , . The problem (3.1) is called a system of generalized nonlinear mixed quasivariational inclusions.
Below are some special cases of the problem (3.1):
-
(A)
If , , and for all , then the problem (3.1) is equivalent to finding such that , , , , , , and
(3.2)
which is called the system of generalized mixed quasivariational inclusions introduced and studied by Peng-Zhu [16], and the problem (3.2) includes those systems of variational inequalities and variational inclusions in [2, 4, 5, 18] as special cases;
-
(B)
If , (the identity map on ), (the identity map on ), for every , for any , and , where
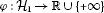 and
and 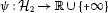 are two proper, convex, lower semi-continuous functionals, is the subdifferential of φ at x, is the subdifferential of ψ at y, then the problem (3.2) reduces to the following system of nonlinear variational inequalities introduced by Cho-Fang-Huang-Hwang [2]: seek such that (3.3)
are two proper, convex, lower semi-continuous functionals, is the subdifferential of φ at x, is the subdifferential of ψ at y, then the problem (3.2) reduces to the following system of nonlinear variational inequalities introduced by Cho-Fang-Huang-Hwang [2]: seek such that (3.3)
In brief, for suitable choices of the mappings presented in the problem (3.1) and the constants ρ, ν, one can obtain various new and previously known systems of variational inequalities and variational inclusions as special cases of the problem (3.1).
Lemma 3.1 Let λ and μ be two positive constants. For each , let be an operator, be a strictly -monotone operator, be a set-valued operator such that for each , is -monotone and is -monotone. Then with , , , , is a solution of the problem (3.1) if and only if

where , and λ, μ are both positive constants.
Proof Observe that

Analogously, we obtain directly that
This completes the proof. □
Based on Lemma 2.3 and Lemma 3.1, we suggest the following two sorts of iterative algorithms for the system of generalized nonlinear mixed quasivariational inclusions (3.1).
Algorithm 3.1 Let λ and μ be two positive constants. For each , let be an operator, be a strictly -monotone operator, be a set-valued operator such that for each , is -monotone and is -monotone.
Step 0: Choose and take , , , . Set .
Step 1: For any , compute by the iterative schemes


Step 2: If , , , , , satisfy Lemma 3.1 to sufficient accuracy, stop; otherwise, set and return to Step 1.
Algorithm 3.2 Let λ and μ be two positive constants. For each and , let be an operator, be a strictly -monotone operator, be set-valued operators such that for each , is -monotone and is -monotone. Given , compute by the iterative schemes
where satisfies (3.5), is a real sequence in and , are two sequences of the elements of and , respectively, which are introduced to take into account possible inexact computation, satisfying
-
(a)
;
-
(b)
, , , , ;
-
(c)
, , , , .
Remark 3.1 Algorithm 3.2 includes several known algorithms in [2–6, 13, 15–18] as special cases.
4 Existence and convergence theorems
At present, we seek those conditions which ensure the existence of solutions for the problem (3.1) and the convergence of the iterative sequence generated by Algorithm 3.1. Furthermore, based on the existence of the solutions for the problem (3.1), the convergence of the Mann perturbed iterative sequence generated by Algorithm 3.2 is discussed.
Theorem 4.1 Let ρ and ν be two positive constants. For , let be Lipschitz continuous with a constant , be strongly -monotone and Lipschitz continuous with constants and , respectively, be Lipschitz continuous with constants and , respectively, be -relaxed monotone with a constant , be strongly monotone with a constant , be set-valued operators such that for each , is -monotone and is -monotone. Let be -Lipschitz continuous with constants , , respectively, and be  -Lipschitz continuous with constants , , respectively. Let be -relaxed monotone in the first argument with a constant , Lipschitz continuous in the first and second arguments with constants and , respectively. Let be -relaxed monotone in the second argument with a constant , Lipschitz continuous in the first and second arguments with constants and , respectively. Assume that is Lipschitz continuous in the first and second arguments with constants and , respectively, is Lipschitz continuous in the first and second arguments with constants and , respectively. Assume that there exist positive constants , , λ and μ satisfying
-Lipschitz continuous with constants , , respectively. Let be -relaxed monotone in the first argument with a constant , Lipschitz continuous in the first and second arguments with constants and , respectively. Let be -relaxed monotone in the second argument with a constant , Lipschitz continuous in the first and second arguments with constants and , respectively. Assume that is Lipschitz continuous in the first and second arguments with constants and , respectively, is Lipschitz continuous in the first and second arguments with constants and , respectively. Assume that there exist positive constants , , λ and μ satisfying


where
Then the problem (3.1) admits a solution and the sequence generated by Algorithm 3.1 converges to as .
Proof Set
Let  . In view of (3.4), (4.1) and Lemma 2.1, we arrive at
. In view of (3.4), (4.1) and Lemma 2.1, we arrive at

By the Lipschitz continuity of and , strong monotonicity of and -relaxed monotonicity of , we obtain that

Note that

Since is Lipschitz continuous, F is relaxed monotone with respect to in the first argument and Lipschitz continuous in the first argument, respectively, , are both Lipschitz continuous, and is -relaxed monotone, we derive that

Since F is Lipschitz continuous in the second argument, we get that
By virtue of the Lipschitz continuity in the first and second arguments of , and  -Lipschitz continuity of A and B, we arrive at
-Lipschitz continuity of A and B, we arrive at

By (4.6)-(4.9), we obtain that
Keeping in mind (4.4), (4.5) and (4.10), we conclude directly that
In a similar way, we see that
Adding the inequalities (4.11) and (4.12), we have
where
In view of (4.2) and (4.14), we know that and so (4.13) implies that , are both Cauchy sequences. Thus, there exist and satisfying and as .
It follows from the Lipschitz continuity of A and (3.5) that
which together with (4.2), (4.13) and (4.14) yields that is a Cauchy sequence. Similarly, we infer that , , are Cauchy sequences as well. Further, there exist such that , , , as . Moreover,

Since is closed, we have . In a similar way, we obtain that , , . On account of the continuity of , , , F, G, , , and Algorithm 3.1, we find that satisfy the following relations:

It follows that is a solution of the problem (3.1) from Lemma 3.1. This completes the proof. □
Remark 4.1 Theorem 4.1 generalizes and unifies those results in [2–6, 13, 15–18] from the following aspects:
(d1) The problem (3.1) includes the variational inequalities and variational inclusions in [2, 15–17] as special cases;
(d2) For every , the -monotone operators and -relaxed monotone operators we utilized here are much more universal than those used in [3, 4, 6, 13, 18];
(d3) Algorithm 3.1 is very different from those in [2–6, 13, 15–18] for finding approximate solutions.
Theorem 4.2 Let ρ, ν, , , , , A, B, C, D, F, G, , , , be the same as in Theorem 4.1. For , let , be set-valued operators such that is -monotone for each fixed , is -monotone for each fixed . Assume that there exist positive constants , , λ and μ satisfying (4.2)-(4.3),
and
Then the problem (3.1) admits a solution and the sequence generated by Algorithm 3.2 converges to as .
Proof It follows from Theorem 4.1 that the problem (3.1) possesses a solution . Further, we get that by Lemma 3.1
where

As in the proof of Theorem 4.1, we conclude that by (3.6) and (4.17)

where . Similarly, we get directly that

where . Adding (4.18) and (4.19), we conclude that

here, and ζ are defined by (4.14). Thus, as and . Hence, for , there exist  such that for every . By (b) and (c) in Algorithm 3.2 and (4.20), we gain that
such that for every . By (b) and (c) in Algorithm 3.2 and (4.20), we gain that

On the grounds of (4.16), (a)-(c) in Algorithm 3.2 and Lemma 2.2, we obtain that and as . The remainder of the proof is the same as that in Theorem 4.1 and is omitted. This completes the proof. □
Remark 4.2 Theorem 4.2 improves and extends those corresponding results in [1, 2, 4, 5, 15–18, 21].
References
Agarwal RP, Huang NJ, Tan MY: Sensitivity analysis for a new system of generalized nonlinear mixed quasivariational inclusions. Appl. Math. Lett. 2004, 17: 345–352. 10.1016/S0893-9659(04)90073-0
Cho YJ, Fang YP, Huang NJ, Hwang HJ: Algorithms for systems of nonlinear variational inequalities. J. Korean Math. Soc. 2004, 41: 489–499.
Fang YP, Huang NJ: H -monotone operator and resolvent operator technique for variational inclusions. Appl. Math. Comput. 2003, 145: 795–803. 10.1016/S0096-3003(03)00275-3
Fang YP, Huang NJ: H -monotone operators and system of variational inclusions. Commun. Appl. Nonlinear Anal. 2004, 11(1):93–101.
Fang YP, Huang NJ, Thompson HB:A new system of variational inclusions withM -monotone operators in Hilbert spaces. Comput. Math. Appl. 2005, 49: 365–374. 10.1016/j.camwa.2004.04.037
Huang NJ, Fang YP: A new class of general variational inclusions involving maximal η -monotone mappings. Publ. Math. (Debr.) 2003, 62(1–2):83–98.
Jin L, Liu Z, Lee BS: Generalized nonlinear multivalued quasivariational inclusions involving relaxed Lipschitz and relaxed monotone mappings. Nonlinear Anal. Forum 2003, 8(1):29–41.
Kazmi KR, Bhat MI: Iterative algorithm for a system of nonlinear variational-like inclusions. Comput. Math. Appl. 2004, 48: 1929–1935. 10.1016/j.camwa.2004.02.009
Liu Z, Debnath L, Kang SM, Ume JS: Generalized mixed quasivariational inclusions and generalized mixed resolvent equations for fuzzy mappings. Appl. Math. Comput. 2004, 149: 879–891. 10.1016/S0096-3003(03)00192-9
Liu Z, Kang SM: Generalized multivalued nonlinear quasivariational inclusions. Math. Nachr. 2003, 253: 45–54. 10.1002/mana.200310044
Liu Z, Kang SM, Ume JS: Completely generalized multivalued strongly quasivariational inequalities. Publ. Math. (Debr.) 2003, 62(1–2):187–204.
Liu Z, Kang SM, Ume JS: Generalized variational inclusions for fuzzy mappings. Adv. Nonlinear Var. Inequal. 2003, 6: 31–40.
Liu Z, Kang SM, Ume JS: On general variational inclusions with noncompact valued mappings. Adv. Nonlinear Var. Inequal. 2002, 5(2):11–25.
Liu Z, Ume JS, Kang SM: General strongly nonlinear quasivariational inequalities with relaxed Lipschitz and relaxed monotone mappings. J. Optim. Theory Appl. 2002, 114(3):639–656. 10.1023/A:1016079130417
Nie HZ, Liu Z, Kim KH, Kang SM: A system of nonlinear variational inequalities involving strongly monotone and pseudocontractive mappings. Adv. Nonlinear Var. Inequal. 2003, 6: 91–99.
Peng JW, Zhu DL:A new system of generalized mixed quasi-variational inclusions with -monotone operators. J. Math. Anal. Appl. 2007, 327: 175–187. 10.1016/j.jmaa.2006.04.015
Wu QH, Liu Z, Shim SH, Kang SM: Approximation-solvability of a new system of nonlinear variational inequalities. Math. Sci. Res. J. 2003, 7(8):338–346.
Yan WY, Fang YP, Huang NJ: A new system of set-valued variational inclusions with H -monotone operators. Math. Inequal. Appl. 2005, 8(3):537–546.
Zeng LC: Iterative algorithm for finding approximate solutions to general strongly nonlinear variational inequalities. J. Math. Anal. Appl. 1994, 187: 352–360. 10.1006/jmaa.1994.1361
Zeng LC, Guo SM, Yao JC: Iterative algorithm for completely generalized set-valued strongly nonlinear mixed variational-like inequalities. Comput. Math. Appl. 2005, 50: 935–945. 10.1016/j.camwa.2004.12.017
Liu LS: Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach spaces. J. Math. Anal. Appl. 1995, 194(1):114–125. 10.1006/jmaa.1995.1289
Nadler SB: Multivalued contraction mappings. Pac. J. Math. 1969, 30: 475–488. 10.2140/pjm.1969.30.475
Acknowledgements
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2012R1A1A2002165).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All the authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, Z., Wang, L., Ume, J.S. et al. Solvability and iterative algorithms for a system of generalized nonlinear mixed quasivariational inclusions with -monotone operators. J Inequal Appl 2012, 235 (2012). https://doi.org/10.1186/1029-242X-2012-235
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-235
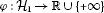 and
and 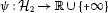 are two proper, convex, lower semi-continuous functionals, is the subdifferential of φ at x, is the subdifferential of ψ at y, then the problem (3.2) reduces to the following system of nonlinear variational inequalities introduced by Cho-Fang-Huang-Hwang [
are two proper, convex, lower semi-continuous functionals, is the subdifferential of φ at x, is the subdifferential of ψ at y, then the problem (3.2) reduces to the following system of nonlinear variational inequalities introduced by Cho-Fang-Huang-Hwang [