Weakly isotone increasing mappings and endpoints in partially ordered metric spaces

Abstract

The aim of this work is to extend the notion of weakly isotone increasing mappings to multivalued and present common endpoint theorems for $\mathcal{T}$-weakly isotone increasing multivalued mappings satisfying generalized $(\psi ,\phi )$-weak contractive as well as almost contractive inequalities in complete partially ordered metric spaces. Examples are given in support of the new results obtained.

MSC:47H10, 54H25, 54H10.

1 Introduction and preliminaries

The Banach contraction principle [1] is a remarkable result in the metric fixed point theory. Over the years, it has been generalized in different directions and spaces by several mathematicians. In 1997, Alber and Guerre-Delabriere [2] introduced the concept of weak contraction in the following way.

Definition 1.1 Let $(\mathcal{X},d)$ be a metric space. A mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ is said to be weakly contractive provided that

$$d(\mathcal{T}x,\mathcal{T}y)\le d(x,y)-\phi (d(x,y)),$$

where $x,y\in \mathcal{X}$ and $\phi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ is a continuous nondecreasing function such that $\phi (t)=0$ if and only if $t=0$.

Using the concept of weak contractiveness, they succeeded in establishing the existence of fixed points for such mappings in Hilbert spaces. Later on, Rhoades [3] proved that the results in [2] are also valid in complete metric spaces. He also proved the following fixed point theorem which is a generalization of the Banach contraction principle.

Theorem 1.2 Let $(\mathcal{X},d)$ be a complete metric space, and let $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ be a weakly contractive mapping. Then $\mathcal{T}$ has a fixed point.

Weak contractive inequalities of the above type have been used to establish fixed point results in a number of subsequent works, some of which are noted in [4, 5]. Since then, fixed point theory for single-valued as well as for multivalued weakly contractive type mappings was studied by many authors. Fixed point theorems for multivalued mappings are quite useful in Control theory and have been frequently used in solving problems in Economics and Game theory.

The development of a geometric fixed point theory for multifunctions was initiated by Nadler [6] in 1969. He used the concept of a Hausdorff metric ℋ to establish the multivalued contraction principle containing the Banach contraction principle as a special case as follows.

Theorem 1.3 Let $(\mathcal{X},d)$ be a complete metric space and $\mathcal{T}$ be a mapping from $\mathcal{X}$ into $CB(\mathcal{X})$ such that for all $x,y\in \mathcal{X}$,

$$\mathcal{H}(\mathcal{T}x,\mathcal{T}y)\le \lambda d(x,y),$$

where $0\le \lambda <1$. Then $\mathcal{T}$ has a fixed point.

Since then, this discipline has been developed further, and many profound concepts and results have been established with considerable generality; see, for example, the works of Itoh and Takahashi [7], Mizoguchi and Takahashi [8], Hussain and Abbas [9], and references cited therein. Very recently, results on common fixed points for a pair of multivalued operators have been obtained by applying various types of contractive conditions; we refer the reader to [10–14]. In some cases, multivalued mapping $\mathcal{T}$ defined on a nonempty set $\mathcal{X}$ assumes a compact value $\mathcal{T}x$ for each x in $\mathcal{X}$. There are situations when, for each x in $\mathcal{X}$, $\mathcal{T}x$ is assumed to be a closed and bounded subset of $\mathcal{X}$. To prove the existence of a fixed point of such mappings, it is essential for mappings to satisfy certain contractive conditions which may involve the Hausdorff metric.

Let $(\mathcal{X},d)$ be a metric space, and let $\mathcal{N}(\mathcal{X})$ (resp. $\mathcal{B}(\mathcal{X})$) be the class of all nonempty (resp. nonempty bounded) subsets of $\mathcal{X}$. We define functions $\mathcal{D}:\mathcal{N}(\mathcal{X})\times \mathcal{N}(\mathcal{X})\to {\mathbb{R}}^{+}$ and $\delta :\mathcal{B}(\mathcal{X})\times \mathcal{B}(\mathcal{X})\to {\mathbb{R}}^{+}$ as follows:

where ${\mathbb{R}}^{+}$ denotes the set of all positive real numbers. For $\mathcal{D}(\{a\},B)$ and $\delta (\{a\},B)$, we write $\mathcal{D}(a,B)$ and $\delta (a,B)$, respectively. Clearly, $\delta (A,B)=\delta (B,A)$. We appeal to the fact that $\delta (A,B)=0$ if and only if $A=B=\{x\}$ for $A,B\in \mathcal{B}(\mathcal{X})$ and

$$0\le \delta (A,B)\le \delta (A,C)+\delta (C,B)$$

for $A,B,C\in \mathcal{B}(\mathcal{X})$. Obviously, for $A=B$, $\delta (A,A)$ reduces to the standard notion of the diameter of a set in a metric space $(\mathcal{X},d)$:

$$diam(A)=\delta (A,A)=sup\{d(x,y):x,y\in \mathcal{A}\}$$

for any subset $A\in \mathcal{B}(\mathcal{X})$.

A point $x\in \mathcal{X}$ is called a fixed point of a multivalued mapping $\mathcal{T}:\mathcal{X}\to \mathcal{N}(\mathcal{X})$ if $x\in \mathcal{T}x$. If there exists a point $x\in \mathcal{X}$ such that $\mathcal{T}x=\{x\}$, then x is called an endpoint of $\mathcal{T}$.

The Fixed Point Theory has developed rapidly in metric spaces endowed with a partial ordering. The first result in this direction was given by Ran and Reurings [[15], Theorem 2.1] who presented its applications to matrix equations. Subsequently, Nieto and Rodríguez-López [16] extended the result of [15] for nondecreasing mappings and applied it to obtain a unique solution for a first-order ordinary differential equation with periodic boundary conditions. Thereafter, several authors obtained many fixed point theorems in ordered metric spaces. In [17], Nashine et al. extended the results in [18] by using $\mathcal{T}$-weakly isotone increasing mappings and relaxing other conditions without taking into account any commutativity condition. Beg and Butt [19] studied set-valued mappings and proved common fixed point results for mappings satisfying implicit relation in a partially ordered metric space. Recently, Amini [20] proved endpoint theorems for multivalued mappings in a metric space. More recently, Choudhury and Metiya [21] as well as Nashine and Kadelburg [22] also proved fixed point theorems for multivalued mappings in the framework of a partially ordered metric space.

We will use the following terminology.

Definition 1.4 Let $\mathcal{X}$ be a nonempty set. Then $(\mathcal{X},d,⪯)$ is called a partially metric space if:

• (i) $(\mathcal{X},d)$ is a metric space,

• (ii) $(\mathcal{X},⪯)$ is a partially ordered set.

Elements $x,y\in \mathcal{X}$ are called comparable if $x⪯y$ or $y⪯x$ holds.

Definition 1.5 ([19])

Let A and B be two nonempty subsets of a partially ordered set $(\mathcal{X},⪯)$. The relation ⪯₁ between A and B is defined as follows:

$$A{⪯}_{1}B⟺\text{for each }a\in A\text{, there exists }b\in B\text{ such that }a⪯b.$$

The purpose of this paper is to prove the existence of a common endpoint for a pair of $\mathcal{T}$-weakly isotone increasing multivalued mappings under a generalized $(\psi ,\phi )$-weakly contractive condition and under a variant of so-called almost contractive conditions of Berinde [23] without using the continuity of any map and any commutativity condition in a complete ordered metric space. Our results generalize the results of Abbas and Ðorić [24], Choudhury and Metiya [21] and Hussain et al. [10] for more general contractive and weakly contractive conditions for a pair of weakly isotone increasing multivalued mappings. They also extend the results of Babu et al. [25], Berinde [23], Choudhury et al. [26] and Ćirić et al. [27] from single-valued mappings in metric spaces to multivalued mappings in ordered metric spaces. Also, the results on common fixed points of weakly isotone increasing mappings in [22] are modified to the results on common endpoints of $\mathcal{T}$-weakly isotone increasing mappings under suitable conditions. Examples are presented to show the usage of the results and, in particular, that the order can be crucial.

2 Common endpoint results under generalized $(\psi ,\phi )$-weak contractive conditions

In this section, we prove common endpoint theorems for a pair of weakly isotone increasing multivalued mappings under a generalized $(\psi ,\phi )$-weak contractive condition. In order to formulate the results, we extend to multivalued mappings the notion of weakly isotone increasing mappings given by Vetro [[28], Definition 4.2].

Definition 2.1 Let $(\mathcal{X},⪯)$ be a partially ordered set and $\mathcal{S},\mathcal{T}:\mathcal{X}\to \mathcal{N}(\mathcal{X})$ be two maps. The mapping $\mathcal{S}$ is said to be $\mathcal{T}$-weakly isotone increasing if $\mathcal{S}x{⪯}_1\mathcal{T}y{⪯}_1\mathcal{S}z$ for all $x\in \mathcal{X}$, $y\in \mathcal{S}x$ and $z\in \mathcal{T}y$.

Note that, for single-valued mappings in particular, $\mathcal{T},\mathcal{S}:\mathcal{X}\to \mathcal{X}$, $\mathcal{S}$ is said to be $\mathcal{T}$-weakly isotone increasing [[28], Definition 2.2] (see also [29]) if for each $x\in \mathcal{X}$ we have $\mathcal{S}x⪯\mathcal{TS}x⪯\mathcal{STS}x$.

Definition 2.2 ([24])

Two set-valued mappings $\mathcal{T},\mathcal{S}:\mathcal{X}\to \mathcal{B}(\mathcal{X})$ are said to satisfy the property of generalized $(\psi ,\phi )$-weak contraction if the inequality

$$\psi (\delta (\mathcal{S}x,\mathcal{T}y))\le \psi (M(x,y))-\phi (M(x,y))$$

(2.1)

holds for all $x,y\in \mathcal{X}$ and for given functions $\psi ,\phi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, where

$$M(x,y)=max\{d(x,y),\delta (x,\mathcal{S}x),\delta (y,\mathcal{T}y),\frac{1}{2}[\mathcal{D}(x,\mathcal{T}y)+\mathcal{D}(y,\mathcal{S}x)]\}.$$

(2.2)

The main result of this section is as follows.

Theorem 2.3 Let $(\mathcal{X},d,⪯)$ be a complete partially ordered metric space, and let $\mathcal{T},\mathcal{S}:\mathcal{X}\to \mathcal{B}(\mathcal{X})$ be two set-valued mappings that satisfy the property of generalized $(\psi ,\phi )$-weak contraction for all comparable $x,y\in \mathcal{X}$, where

• (a) ψ is a continuous nondecreasing function with $\psi (t)=0$ if and only if $t=0$,

• (b) φ is a lower semicontinuous function with $\phi (t)=0$ if and only if $t=0$.

Also, suppose that $\mathcal{S}$ is $\mathcal{T}$-weakly isotone increasing and there exists an $x_0\in \mathcal{X}$ such that $\{x_0\}{⪯}_1\mathcal{S}{x}_0$. Assume the condition

$$\{\begin{array}{c}\mathit{\text{if}}\{x_n\}\subset \mathcal{X}\mathit{\text{is a non-decreasing sequence with}}{x}_n\to z\mathit{\text{in}}\mathcal{X},\hfill \\ \mathit{\text{then}}{x}_n⪯z\mathit{\text{for all}}n.\hfill \end{array}$$

(2.3)

Then there exists a common endpoint $u\in \mathcal{X}$ of $\mathcal{T}$ and $\mathcal{S}$, i.e. $\{u\}=\mathcal{T}u=\mathcal{S}u$.

Proof First of all, we show that if $\mathcal{S}$ or $\mathcal{T}$ has an endpoint, then it is a common endpoint of $\mathcal{S}$ and $\mathcal{T}$. Indeed, let, e.g., z be an endpoint of $\mathcal{S}$. If we use the inequality (2.1) for $x=y=z$, we have

$$\begin{array}{rcl}\psi (\delta (z,\mathcal{T}z))& =& \psi (\delta (\mathcal{S}z,\mathcal{T}z))\\ \le & \psi (M(z,z))-\phi (M(z,z))\\ =& \psi (\delta (z,\mathcal{T}z))-\phi (\delta (z,\mathcal{T}z)),\end{array}$$

and we conclude that $\delta (z,\mathcal{T}z)=0$ and $\{z\}=\mathcal{T}z$. Therefore, z is a common endpoint of $\mathcal{S}$ and $\mathcal{T}$.

We will define a sequence $\{x_n\}\subset \mathcal{X}$ and prove that the limit point of that sequence is a unique common endpoint for $\mathcal{T}$ and $\mathcal{S}$. For a given $x_0\in \mathcal{X}$ and a nonnegative integer n, let

$$x_{2n+1}\in \mathcal{S}{x}_{2n}:={\mathcal{A}}_{2n}\text{and}{x}_{2n+2}\in \mathcal{T}{x}_{2n+1}:={\mathcal{A}}_{2n+1},$$

and let

$$a_n=\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}),c_n=d(x_n,x_{n+1}).$$

(2.4)

If $x_{n_0}\in \mathcal{S}{x}_{n_0}$ or $x_{n_0}\in \mathcal{T}{x}_{n_0}$ for some $n_0$, then the proof is finished. So, assume $x_n\ne x_{n+1}$ for all n.

Since $\{x_0\}{⪯}_1\mathcal{S}{x}_0$, $x_1\in \mathcal{S}{x}_0$ can be chosen so that $x_0⪯x_1$. Since $\mathcal{S}$ is $\mathcal{T}$-weakly isotone increasing, it is $\mathcal{S}{x}_0{⪯}_1\mathcal{T}{x}_1$; in particular, $x_2\in \mathcal{T}{x}_1$ can be chosen so that $x_1⪯x_2$. Now, $\mathcal{T}{x}_1{⪯}_1\mathcal{S}{x}_2$ (since $x_2\in \mathcal{T}{x}_1$); in particular, $x_3\in \mathcal{S}{x}_2$ can be chosen so that $x_2⪯x_3$.

Continuing this process, we conclude that $\{x_n\}$ can be an increasing sequence in $\mathcal{X}$:

$$x_1⪯x_2⪯\cdots ⪯x_n⪯x_{n+1}⪯\cdots .$$

The sequences $\{a_n\}$ and $\{c_n\}$ are convergent. Suppose that n is an odd number. Substituting $x=x_{n+1}$ and $y=x_n$ in (2.1) and using the properties of functions ψ and φ, we obtain

$$\begin{array}{rcl}\psi (\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}))& =& \psi (\delta (\mathcal{T}{x}_n,\mathcal{S}{x}_{n+1}))\\ \le & \psi (M(x_n,x_{n+1}))-\phi (M(x_n,x_{n+1}))\\ \le & \psi (M(x_n,x_{n+1})),\end{array}$$

which implies that

$$\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})\le M(x_n,x_{n+1}).$$

(2.5)

Now, from (2.2) and from the triangle inequality for δ, we have

$$\begin{array}{rcl}M(x_n,x_{n+1})& =& max\{d(x_n,x_{n+1}),\delta (\mathcal{T}{x}_n,x_n),\delta (\mathcal{S}{x}_{n+1},x_{n+1}),\\ \frac{1}{2}[\mathcal{D}(\mathcal{T}{x}_n,x_{n+1})+\mathcal{D}(\mathcal{S}{x}_{n+1},x_n)]\}\\ \le & max\{\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n),\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n),\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n),\\ \frac{1}{2}[\mathcal{D}(\mathcal{T}{x}_n,x_{n+1})+\mathcal{D}(\mathcal{S}{x}_{n+1},x_n)]\}\\ \le & max\{\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n),\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n),\frac{1}{2}\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_{n-1})\}\\ \le & max\{\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n),\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n),\frac{1}{2}[\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n-1})+\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})]\}\\ =& max\{\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n),\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n)\}.\end{array}$$

Now, if $\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)<\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n)$, then

$$M(x_n,x_{n+1})\le \delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n).$$

(2.6)

From (2.5) and (2.6), it follows that

$$M(x_n,x_{n+1})=\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n)>\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)\ge 0.$$

It, furthermore, implies that

$$\begin{array}{rcl}\psi (\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}))& =& \psi (\delta (\mathcal{T}{x}_n,\mathcal{S}{x}_{n+1}))\\ \le & \psi (M(x_n,x_{n+1}))-\phi (M(x_n,x_{n+1}))\\ <& \psi (M(x_n,x_{n+1}))\\ =& \psi (\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n)),\end{array}$$

a contradiction. So, we have

$$\delta ({\mathcal{A}}_{n+1},{\mathcal{A}}_n)\le M(x_n,x_{n+1})\le \delta ({\mathcal{A}}_n,{\mathcal{A}}_{n-1}).$$

(2.7)

In a similar way, we can establish the inequality (2.7) when n is an even number. Therefore, the sequence $\{a_n\}$ defined in (2.4) is nonincreasing and bounded. Let $a_n\to a$ when $n\to \mathrm{\infty }$. From (2.7), we have

$$\underset{n\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})=\underset{n\to \mathrm{\infty }}{lim}M(x_n,x_{n+1})=a\ge 0.$$

Passing to the (upper) limit as $n\to \mathrm{\infty }$,

$$\underset{n\to \mathrm{\infty }}{lim}\psi (\delta ({\mathcal{A}}_{2n},{\mathcal{A}}_{2n+1}))\le \underset{n\to \mathrm{\infty }}{lim}\psi (M(x_{2n},x_{2n+1}))-\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\phi (M(x_{2n},x_{2n+1})),$$

and since φ is lower semicontinuous, we have

$$\psi (a)\le \psi (a)-\phi (a),$$

a contradiction unless $a=0$. Hence,

$$\underset{n\to \mathrm{\infty }}{lim}{a}_n=\underset{n\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})=0.$$

(2.8)

From (2.8) and (2.4), it follows that

$$\underset{n\to \mathrm{\infty }}{lim}{c}_n=\underset{n\to \mathrm{\infty }}{lim}d(x_n,x_{n+1})=0.$$

Next, we prove that the sequence $\{x_n\}$ is a Cauchy sequence. For this, we first prove that for each $ϵ>0$, there exists $n_0(ϵ)$ such that

$$m>n\ge n_0\Rightarrow \delta ({\mathcal{A}}_{2m},{\mathcal{A}}_{2n})<ϵ.$$

(2.9)

We proceed by negation and suppose that the inequality in (2.9) is not true. That is, there exists $ϵ>0$ for which we can find nonnegative integer sequences $\{m(k)\}$ and $\{n(k)\}$ such that $n(k)$ is the smallest element of the sequence $\{n(k)\}$ such that for each $k\in \mathbb{N}$,

$$n(k)>m(k)>k,\delta ({\mathcal{A}}_{2m(k)},{\mathcal{A}}_{2n(k)})\ge ϵ.$$

This means that

$$\delta ({\mathcal{A}}_{2m(k)},{\mathcal{A}}_{2n(k)-2})<ϵ.$$

(2.10)

From (2.10) and the triangle inequality for δ, we have

$$\begin{array}{rcl}ϵ& \le & \delta ({\mathcal{A}}_{2m(k)},{\mathcal{A}}_{2n(k)})\\ \le & \delta ({\mathcal{A}}_{2m(k)},{\mathcal{A}}_{2n(k)-2})+\delta ({\mathcal{A}}_{2n(k)-2},{\mathcal{A}}_{2n(k)-1})+\delta ({\mathcal{A}}_{2n(k)-1},{\mathcal{A}}_{2n(k)})\\ <& ϵ+\delta ({\mathcal{A}}_{2n(k)-2},{\mathcal{A}}_{2n(k)-1})+\delta ({\mathcal{A}}_{2n(k)-1},{\mathcal{A}}_{2n(k)}).\end{array}$$

Passing to the limit as $k\to \mathrm{\infty }$ and using (2.8), we can conclude that

$$\underset{k\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{2m(k)},{\mathcal{A}}_{2n(k)})=ϵ.$$

(2.11)

We note that

Using (2.8) and (2.11), we get

$$\underset{k\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2n(k)})=\underset{k\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{2m(k)},{\mathcal{A}}_{2n(k)-1})=ϵ,$$

(2.12)

and from

$$|\delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2n(k)+1})-\delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2n(k)})|\le \delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2n(k)-1}),$$

using (2.8) and (2.12), we get

$$\underset{k\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2n(k)-1})=ϵ.$$

Also, from (2.2), (2.8) and (2.12), we have

$$\underset{k\to \mathrm{\infty }}{lim}M(x_{2m(k)},x_{2n(k)+1})=ϵ.$$

(2.13)

Putting $x=x_{2m(k)}$, $y=x_{2n(k)+1}$ in (2.1), we have

$$\begin{array}{rcl}\psi (\delta ({\mathcal{A}}_{2m(k)},{\mathcal{A}}_{2n(k)+1}))& =& \psi (\delta (\mathcal{T}{x}_{2n(k)+1},\mathcal{S}{x}_{2m(k)}))\\ \le & \psi (M(x_{2m(k)},x_{2n(k)+1}))-\phi (M(x_{2m(k)},x_{2n(k)+1})).\end{array}$$

Passing to the (upper) limit as $k\to \mathrm{\infty }$ and using (2.12), (2.13), we get

$$\psi (ϵ)\le \psi (ϵ)-\phi (ϵ),$$

a contradiction to $ϵ>0$. Therefore, the conclusion (2.9) is true. From the construction of the sequence $\{x_n\}$, it follows that the same conclusion holds for $\{x_n\}$. Thus, for each $ϵ>0$ there exists $n_0(ϵ)$ such that

$$m,n\ge n_0\Rightarrow d(x_{2m},x_{2n})<ϵ.$$

(2.14)

From (2.4) and (2.14), we conclude that $\{x_n\}$ is a Cauchy sequence in $(\mathcal{X},d)$ which is complete. So, there exists $u\in \mathcal{X}$ such that

$$\underset{n\to \mathrm{\infty }}{lim}{x}_n=u.$$

To prove that u is an endpoint of $\mathcal{S}$, suppose that $\delta (u,\mathcal{S}u)>0$. From (2.3), we have $x_{2n+1}⪯u$ for all $n\in \mathbb{N}$. As the limit point u is independent of the choice of $x_n\in {\mathcal{A}}_n$, we also get

$$\underset{n\to \mathrm{\infty }}{lim}\delta (\mathcal{S}{x}_{2n},u)=\underset{n\to \mathrm{\infty }}{lim}\delta (\mathcal{T}{x}_{2n+1},u)=0.$$

(2.15)

From

$$\begin{array}{rcl}M(u,x_{2n+1})& =& max\{d(u,x_{2n+1}),\delta (u,\mathcal{S}u),\delta (\mathcal{T}{x}_{2n+1},x_{2n+1}),\\ \frac{1}{2}[\mathcal{D}(\mathcal{S}u,x_{2n+1})+\mathcal{D}(\mathcal{T}{x}_{2n+1},u)]\},\end{array}$$

we have $M(u,x_{2n+1})\to \delta (u,\mathcal{S}u)$ as $n\to \mathrm{\infty }$. Since

$$\psi (\delta (\mathcal{S}u,\mathcal{T}{x}_{2n+1}))\le \psi (M(u,x_{2n+1}))-\phi (M(u,x_{2n+1}))$$

passing to the (upper) limit as $n\to \mathrm{\infty }$ and using (2.15), we obtain

$$\psi (\delta (\mathcal{S}u,u))\le \psi (\delta (\mathcal{S}u,u))-\phi (\delta (\mathcal{S}u,u)),$$

which implies $\phi (\delta (\mathcal{S}u,u))=0$. Hence, $\delta (\mathcal{S}u,u)=0$ and $\mathcal{S}u=\{u\}$ and this proves that u is an endpoint of $\mathcal{S}$ and also an endpoint of $\mathcal{T}$. The proof is completed. □

If $\mathcal{T}$ and $\mathcal{S}$ are two single-valued mappings, then we obtain the following consequence.

Corollary 2.4 Let $(\mathcal{X},d,⪯)$ be a complete partially ordered metric space, and let $\mathcal{T},\mathcal{S}:\mathcal{X}\to \mathcal{X}$ be two mappings that satisfy, for all comparable $x,y\in \mathcal{X}$,

$$\psi (d(\mathcal{T}x,\mathcal{S}y))\le \psi (M(x,y))-\phi (M(x,y)),$$

where φ, ψ are as in Theorem  2.3 and

$$M(x,y)=max\{d(x,y),d(\mathcal{T}x,x),d(y,\mathcal{S}y),\frac{1}{2}[d(y,\mathcal{T}x)+d(x,\mathcal{S}y)]\}.$$

Also, suppose that $\mathcal{S}$ is $\mathcal{T}$-weakly isotone increasing. If the condition (2.3) holds, then $\mathcal{S}$ and $\mathcal{T}$ have a common fixed point $z\in \mathcal{X}$, i.e., $\mathcal{S}z=\mathcal{T}z=z$.

Putting $\mathcal{S}=\mathcal{T}$ in Theorem 2.3, we obtain the following

Corollary 2.5 Let $(\mathcal{X},d,⪯)$ be a complete partially ordered metric space, and let $\mathcal{T}:\mathcal{X}\to \mathcal{B}(\mathcal{X})$ be a set-valued mapping that satisfies

$$\psi (\delta (\mathcal{T}x,\mathcal{T}y))\le \psi (M(x,y))-\phi (M(x,y)),$$

(2.16)

for all comparable $x,y\in \mathcal{X}$, where

$$M(x,y)=max\{d(x,y),\delta (x,\mathcal{T}x),\delta (y,\mathcal{T}y),\frac{1}{2}[\mathcal{D}(x,\mathcal{T}y)+\mathcal{D}(y,\mathcal{T}x)]\}$$

and where φ, ψ are as in Theorem  2.3. Also, suppose that $\mathcal{T}x{⪯}_1\mathcal{T}(\mathcal{T}x)$ for all $x\in \mathcal{X}$ and there is $x_0\in \mathcal{X}$ such that $\{x_0\}{⪯}_1\mathcal{T}{x}_0$. If the condition (2.3) holds, then there exists an endpoint $u\in \mathcal{X}$ of $\mathcal{T}$, i.e., that $\{u\}=\mathcal{T}u$.

If $\mathcal{T}$ is a single-valued mapping in Corollary 2.5, then we have the following

Corollary 2.6 Let $(\mathcal{X},d,⪯)$ be a complete partially ordered metric space, and let $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ be a mapping that satisfies, for all comparable $x,y\in \mathcal{X}$,

$$\psi (d(\mathcal{T}x,\mathcal{T}y))\le \psi (M(x,y))-\phi (M(x,y)),$$

(2.17)

where φ, ψ are as in Theorem  2.3 and

$$M(x,y)=max\{d(x,y),d(\mathcal{T}x,x),d(y,\mathcal{T}y),\frac{1}{2}[d(y,\mathcal{T}x)+d(x,\mathcal{T}y)]\}.$$

Also, suppose that $\mathcal{T}x⪯\mathcal{T}(\mathcal{T}x)$ for all $x\in \mathcal{X}$. If the condition (2.3) holds, then $\mathcal{T}$ has a fixed point $z\in \mathcal{X}$, i.e., $\mathcal{T}z=z$.

Remark 2.7 In [[15], Corollary 2.5], it was proved that if

$$\text{every pair of elements has a lower bound and an upper bound,}$$

(2.18)

then for every $x\in \mathcal{X}$,

$$\underset{n\to \mathrm{\infty }}{lim}{\mathcal{T}}^n(x)=y,$$

where y is a fixed point of $\mathcal{T}$ such that

$$y=\underset{n\to \mathrm{\infty }}{lim}{\mathcal{T}}^n(x_0),$$

and hence $\mathcal{T}$ has a unique fixed point. If the condition (2.18) fails, it is possible to find examples of mappings $\mathcal{T}$ with more than one fixed point (cf. [16]).

We illustrate the results of this section with two simple examples. The first one shows how a multivalued variant (Corollary 2.5) can be used. The other shows that (in the single-valued case) the use of order can be crucial.

Example 2.8 Let $\mathcal{X}=\{A,B,C\}$, where $A=(0,0)$, $B=(1,1)$, $C=(2,0)\in {\mathbb{R}}^2$. Metric d is defined as $d((x_1,y_1),(x_2,y_2))=max\{|x_1-x_2|,|y_1-y_2|\}$ so that $d(A,B)=1$, $d(A,C)=2$ and $d(B,C)=1$. Order ⪯ is introduced by $(x_1,y_1)⪯(x_2,y_2)$ iff $x_1\ge x_2$ and $y_1\ge y_2$, so that $A⪰B$ and $A⪰C$, while B and C are incomparable.

Consider the mapping $\mathcal{T}:\mathcal{X}\to \mathcal{B}(\mathcal{X})$ given by

$$\mathcal{T}=\left(\begin{array}{ccc}A& B& C\\ \{A\}& \{A\}& \{A,B\}\end{array}\right),$$

and functions $\psi ,\phi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ given by $\psi (t)=\frac{1}{2}t$, $\phi (t)=\frac{1}{4}t$. To prove that the condition (2.16) of Corollary 2.5 holds, it is enough to check that it is satisfied for $x=A$, $y=B$ and for $x=A$, $y=C$ (in the case when $x=y$ (2.16) is trivially satisfied).

If $x=A$, $y=B$, then $\mathcal{T}x=\mathcal{T}y=\{A\}$ and $\delta (\mathcal{T}x,\mathcal{T}y)=0$, $M(x,y)=d(A,B)=1$, so (2.16) holds. If $x=A$, $y=C$, then

$$\delta (\mathcal{T}x,\mathcal{T}y)=\delta (\{A\},\{A,B\})=d(A,B)=1,$$

and

$$\begin{array}{rcl}M(x,y)& =& max\{d(A,C),\delta (A,\{A\}),\delta (C,\{A,B\}),\frac{1}{2}(\mathcal{D}(A,\{A,B\})+\mathcal{D}(C,\{A\}))\}\\ =& max\{2,0,2,\frac{1}{2}(0+2)\}=2.\end{array}$$

Hence, $\psi (\delta (\mathcal{T}x,\mathcal{T}y))=\frac{1}{2}\le 1-\frac{1}{2}=\psi (M(x,y))-\phi (M(x,y))$. Note also that $\mathcal{T}x{⪯}_1\mathcal{T}(\mathcal{T}x)$ holds for all $x\in \mathcal{X}$ (only the case $x=C$ is nontrivial, when $\mathcal{T}x=\{A,B\}$, $\mathcal{T}(\mathcal{T}x)=\{A\}$, and for $B\in \mathcal{T}x$, there is $A\in \mathcal{T}(\mathcal{T}x)$ such that $B⪯A$). All other conditions of Corollary 2.5 are fulfilled and $\mathcal{T}$ has an endpoint A.

Example 2.9 Consider the same partially ordered metric space $(\mathcal{X},d,⪯)$ as in the previous example and the mapping $\mathcal{T}:\mathcal{X}\to \mathcal{X}$ defined by

$$\mathcal{T}=\left(\begin{array}{ccc}A& B& C\\ A& A& B\end{array}\right).$$

Let again $\psi ,\phi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ be given by $\psi (t)=\frac{1}{2}t$, $\phi (t)=\frac{1}{4}t$. It is again easy to show that in the cases $x=A$, $y=B$, as well as $x=A$, $y=C$, the condition (2.17) of Corollary 2.6 is satisfied, and it follows that $\mathcal{T}$ has a fixed point A. However, for (incomparable) points $x=B$, $y=C$, the condition (2.17) is not satisfied, and so the respective result in the metric space without order cannot be applied to reach the conclusion. Indeed, in this case, $\mathcal{T}x=A$, $\mathcal{T}y=B$,

and $\psi (d(\mathcal{T}x,\mathcal{T}y))=\frac{1}{2}>\frac{1}{4}=\psi (M(x,y))-\phi (M(x,y))$.

3 Common endpoint for almost contractive conditions

In this section, we prove common endpoint theorems for $\mathcal{T}$-weakly isotone increasing multivalued mappings satisfying a variant of an almost contractive condition.

Theorem 3.1 Let $(\mathcal{X},d,⪯)$ be a complete partially ordered metric space. Assume that there is a continuous function $\phi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ with $\phi (t)<t$ for each $t>0$, $\phi (0)=0$ and that $\mathcal{T},\mathcal{S}:\mathcal{X}\to \mathcal{B}(\mathcal{X})$ are multivalued mappings such that

$$\delta (\mathcal{T}x,\mathcal{S}y)\le M(x,y)+Lmin\{\phi (\delta (x,\mathcal{T}x)),\phi (\delta (y,\mathcal{S}y)),\phi (\delta (x,\mathcal{S}y)),\phi (\delta (y,\mathcal{T}x))\},$$

(3.1)

for all comparable $x,y\in \mathcal{X}$, where $L\ge 0$, and

$$M(x,y)=max\{\phi (d(x,y)),\phi (\delta (x,\mathcal{T}x)),\phi (\delta (y,\mathcal{S}y)),\phi \left(\frac{\mathcal{D}(x,\mathcal{S}y)+\mathcal{D}(y,\mathcal{T}x)}{2}\right)\}.$$

(3.2)

Also, suppose that $\mathcal{S}$ is $\mathcal{T}$-weakly isotone increasing and there exists an $x_0\in \mathcal{X}$ such that $\{x_0\}{⪯}_1\mathcal{S}{x}_0$. If the condition (2.3) holds, then $\mathcal{S}$ and $\mathcal{T}$ have a common endpoint.

Proof First of all, we show that if $\mathcal{S}$ or $\mathcal{T}$ has an endpoint, then it is a common endpoint of $\mathcal{S}$ and $\mathcal{T}$. Indeed, let z be an endpoint of $\mathcal{S}$ and assume $\delta (z,\mathcal{T}z)>0$. If we use the inequality (3.1) for $x=y=z$ and the properties of φ, we have

a contradiction. Thus $\delta (z,\mathcal{T}z)=0$, and so z is a common endpoint of $\mathcal{S}$ and $\mathcal{T}$.

Let $x\in \mathcal{X}$ be arbitrary. Define a sequence $\{x_n\}\subset \mathcal{X}$ as follows:

$$x_0=x,x_{2n+1}\in \mathcal{S}{x}_{2n}:={\mathcal{A}}_{2n},x_{2n+2}\in \mathcal{T}{x}_{2n+1}:={\mathcal{A}}_{2n+1}\text{for }n\ge 0.$$

(3.3)

If $x_{n_0}\in \mathcal{S}{x}_{n_0}$ or $x_{n_0}\in \mathcal{T}{x}_{n_0}$ for some $n_0$, then the proof is finished. So, assume $x_n\ne x_{n+1}$ for all n.

Since $\{x_0\}{⪯}_1\mathcal{S}{x}_0$, $x_1\in \mathcal{S}{x}_0$ can be chosen so that $x_0⪯x_1$. Since $\mathcal{S}$ is $\mathcal{T}$-weakly isotone increasing, it is $\mathcal{S}{x}_0{⪯}_1\mathcal{T}{x}_1$; in particular, $x_2\in \mathcal{T}{x}_1$ can be chosen so that $x_1⪯x_2$. Now, $\mathcal{T}{x}_1{⪯}_1\mathcal{S}{x}_2$ (since $x_2\in \mathcal{T}{x}_1$); in particular, $x_3\in \mathcal{S}{x}_2$ can be chosen so that $x_2⪯x_3$.

Continuing this process, we conclude that $\{x_n\}$ can be an increasing sequence in $\mathcal{X}$:

$$x_1⪯x_2⪯\cdots ⪯x_n⪯x_{n+1}⪯\cdots .$$

(3.4)

If there exists a positive integer N such that $x_N=x_{N+1}$, then $x_N$ is a common endpoint of $\mathcal{T}$ and $\mathcal{S}$. Hence, we shall assume that $x_n\ne x_{n+1}$ for all $n\ge 0$.

Now, we claim that for all $n\in \mathbb{N}$, we have

$$\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})<\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n).$$

(3.5)

From (3.4), we have that $x_n\prec x_{n+1}$ for all $n\in \mathbb{N}$. Then from (3.1) with $x=x_n$, $y=x_{n+1}$ and $n=2k-1$, $k\in \mathbb{N}$, we get

(3.6)

By (3.2), we have

If $M(x_n,x_{n+1})=\phi (\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}))$, by (3.6) and using the fact that $\phi (t)<t$ for all $t>0$, we have

$$\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})\le \phi (\mathcal{A}(x_n,{\mathcal{A}}_{n+1}))<\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}),$$

a contradiction.

If $M(x_n,x_{n+1})=\phi (\frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_{n+1}))$, we get

$$\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})\le \phi (\frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_{n+1}))<\frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_{n+1}).$$

On the other hand, by the triangular inequality, we have

$$\frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_{n+1})\le \frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)+\frac{1}{2}\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}).$$

Thus, we have

$$\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})<\frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)+\frac{1}{2}\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}),$$

which implies that

$$\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})<\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n).$$

If $M(x_n,x_{n+1})=\phi (\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n))$, we get

$$\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})\le \phi (\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n))<\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n).$$

Thus, in all cases, we have $\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1})<\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)$ for all $n=2k-1$, $k\in \mathbb{N}$. Similarly, we can prove that $\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)<\delta ({\mathcal{A}}_{n-2},{\mathcal{A}}_{n-1})$ for all $n=2k$, $k\in \mathbb{N}$. Therefore, we conclude that (3.5) holds.

Now, from (3.5), it follows that the sequence $\{\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)\}$ is decreasing. Therefore, there is some $\lambda \ge 0$ such that

$$\underset{n\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)=\lambda .$$

(3.7)

We are able to prove that $\lambda =0$. In fact, by the triangular inequality, we get

$$\frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_{n+1})\le \frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)+\frac{1}{2}\delta ({\mathcal{A}}_n,{\mathcal{A}}_{n+1}).$$

By (3.5), we have

$$\frac{1}{2}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_{n+1})\le \delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n).$$

(3.8)

From (3.8), taking the upper limit as $n\to \mathrm{\infty }$, we get

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{1}{2}\delta ({\mathcal{A}}_{2n-1},{\mathcal{A}}_{2n+1})\le \underset{n\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{2n-1},{\mathcal{A}}_{2n}).$$

If we set

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{1}{2}\delta ({\mathcal{A}}_{2n-1},{\mathcal{A}}_{2n+1})=b,$$

(3.9)

then clearly $0\le b\le \lambda$. As φ is continuous, taking the upper limit on both sides of (3.6), we get

$$\begin{array}{rcl}\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}sup}\delta ({\mathcal{A}}_{2n},{\mathcal{A}}_{2n+1})& \le & max\{\phi (\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}sup}\delta ({\mathcal{A}}_{2n},{\mathcal{A}}_{2n+1})),\phi (\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}sup}\delta ({\mathcal{A}}_{2n},{\mathcal{A}}_{2n-1})),\\ \phi \left(\frac{1}{2}(\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}sup}\delta ({\mathcal{A}}_{2n-1},{\mathcal{A}}_{2n+1}))\right)\}.\end{array}$$

Hence, by (3.7) and (3.9), we deduce

$$\lambda \le max\{\phi (\lambda ),\phi (b)\}.$$

If we suppose that $\lambda >0$, then we have

$$\lambda \le max\{\phi (\lambda ),\phi (b)\}<max\{\lambda ,b\}=\lambda ,$$

a contradiction. Thus $\lambda =0$, and consequently,

$$\underset{n\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{n-1},{\mathcal{A}}_n)=0.$$

(3.10)

From (3.3) and (3.10), it follows that

$$\underset{n\to \mathrm{\infty }}{lim}d(x_n,x_{n+1})=0.$$

(3.11)

Now, we prove that $\{x_n\}$ is a Cauchy sequence. To this end, it is sufficient to verify that $\{x_{2n}\}$ is a Cauchy sequence. Suppose, on the contrary, that it is not. Then there exists an $\epsilon >0$ such that for each even integer 2k there are even integers $2n(k)$, $2m(k)$ with $2m(k)>2n(k)>2k$ such that

$$r_k=\delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2m(k)})\ge \epsilon \text{for }k\in \{1,2,\dots \}.$$

(3.12)

For every even integer 2k, let $2m(k)$ be the smallest number exceeding $2n(k)$ satisfying the condition (3.12) for which

$$\delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2m(k)-2})<\epsilon .$$

(3.13)

From (3.12), (3.13) and the triangular inequality, we have

$$\begin{array}{rcl}\epsilon & \le & r_k\le \delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2m(k)-2})+\delta ({\mathcal{A}}_{2m(k)-2},{\mathcal{A}}_{2m(k)-1})+\delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2m(k)})\\ \le & \epsilon +\delta ({\mathcal{A}}_{2m(k)-2},{\mathcal{A}}_{2m(k)-1})+\delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2m(k)}).\end{array}$$

Hence, by (3.10), it follows that

$$\underset{k\to \mathrm{\infty }}{lim}{r}_k=\epsilon .$$

(3.14)

Now, from the triangular inequality, we have

$$|\delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2m(k)-1})-\delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2m(k)})|\le \delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2m(k)}).$$

Passing to the limit as $k\to \mathrm{\infty }$ and using (3.10) and (3.14), we get

$$\underset{k\to \mathrm{\infty }}{lim}\delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2m(k)-1})=\epsilon .$$

(3.15)

On the other hand, we have

(3.16)

where

From

taking the upper limit as $k\to \mathrm{\infty }$, using (3.10) and (3.14), we get

$$\underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\delta ({\mathcal{A}}_{2m(k)-2},{\mathcal{A}}_{2n(k)})\le \epsilon .$$

On the other hand, we have

$$\begin{array}{rl}\epsilon & \le \delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2n(k)-1})\\ \le \delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2m(k)-2})+\delta ({\mathcal{A}}_{2m(k)-2},{\mathcal{A}}_{2n(k)})+\delta ({\mathcal{A}}_{2n(k)},{\mathcal{A}}_{2n(k)-1}),\end{array}$$

and taking the lower limit as $k\to \mathrm{\infty }$, we get

$$\epsilon \le \underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\delta ({\mathcal{A}}_{2m(k)-1},{\mathcal{A}}_{2n(k)-1})\le \underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}d({\mathcal{A}}_{2m(k)-2},{\mathcal{A}}_{2n(k)}).$$

It follows that

$$\epsilon \le \underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\delta ({\mathcal{A}}_{2m(k)-2},{\mathcal{A}}_{2n(k)}),$$

and so

$$\underset{k\to \mathrm{\infty }}{lim}\delta (x_{2m(k)-2},{\mathcal{A}}_{2n(k)})=\epsilon .$$

(3.17)

Now, using (3.10), (3.14), (3.15), (3.17) and the continuity of φ, we get

$$\underset{k\to \mathrm{\infty }}{lim}M(x_{2m(k)-1},x_{2n(k)})=max\{\phi (\epsilon ),0,0,\phi (\epsilon )\}=\phi (\epsilon ).$$

(3.18)

Passing to the limit as $k\to \mathrm{\infty }$ in (3.16), we obtain

$$\epsilon \le \phi (\epsilon )<\epsilon ,$$

a contradiction. Thus, the assumption (3.12) is wrong. Hence, $\{x_n\}$ is a Cauchy sequence. From the completeness of $\mathcal{X}$, there exists a $z\in \mathcal{X}$ such that

$$\underset{n\to \mathrm{\infty }}{lim}{x}_n=z.$$

As the limit point z is independent of the choice of $x_n\in {\mathcal{A}}_n$, we also get

$$\underset{n\to \mathrm{\infty }}{lim}\delta (\mathcal{S}{x}_{2n},z)=\underset{n\to \mathrm{\infty }}{lim}\delta (\mathcal{T}{x}_{2n+1},z)=0.$$

Now, we show that z is a common endpoint of $\mathcal{S}$ and $\mathcal{T}$.

Suppose, to the contrary, that $\delta (z,Sz)>0$. By the assumption (2.3), $x_n⪯z$ for all n. Then using the triangular inequality for δ and taking $x=x_{2n+1}$ and $y=z$ in (3.1), we have

$$\begin{array}{rcl}\delta (z,Sz)& \le & \delta (z,T{x}_{2n+1})+\delta (\mathcal{T}{x}_{2n+1},\mathcal{S}z)\\ \le & \delta (z,T{x}_{2n+1})+max\{\phi (d(x_{2n+1},z)),\phi (\delta (x_{2n+1},\mathcal{T}{x}_{2n+1})),\phi (\delta (z,\mathcal{S}z)),\\ \phi \left(\frac{\mathcal{D}(z,\mathcal{T}{x}_{2n+1})+\mathcal{D}(x_{2n+1},\mathcal{S}z)}{2}\right)\}+Lmin\{\phi (\delta (x_{2n+1},\mathcal{T}{x}_{2n+1})),\\ \phi (\delta (z,\mathcal{S}z)),\phi (\delta (x_{2n+1},\mathcal{S}z)),\phi (\delta (z,\mathcal{T}{x}_{2n+1}))\}.\end{array}$$

Passing to the limit as $n\to \mathrm{\infty }$ and using the properties of φ, we have

$$\delta (z,\mathcal{S}z)\le max\{\phi (\delta (z,\mathcal{S}z)),\phi (\delta (z,\mathcal{S}z)/2)\}<\delta (z,\mathcal{S}z),$$

a contradiction. Hence, $\delta (z,\mathcal{S}z)=0$, and so $\{z\}=\mathcal{S}z$. It follows that z is an endpoint of $\mathcal{S}$, and also of $\mathcal{T}$. This finishes the proof. □

Remark 3.2

• (i) The condition

  

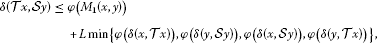  (3.19)

where

$$M_1(x,y)=max\{d(x,y),\delta (x,\mathcal{T}x),\delta (y,\mathcal{S}y),\frac{\mathcal{D}(y,\mathcal{T}x)+\mathcal{D}(x,\mathcal{S}y)}{2}\},$$

implies the condition (3.1).

• (ii) The condition (3.19) is equivalent to the condition (3.1) if we suppose that φ is a non-decreasing function.

• (iii) From Theorem 3.1 we can derive a corollary involving the condition (3.19).

• (iv) Under the hypothesis that φ is a non-decreasing function, we can state many other corollaries using the equivalences established by Jachymski in [30] for single-valued mappings.

Example 3.3 Let $\mathcal{X}=[0,+\mathrm{\infty })$ be equipped with the standard metric d and order ⪯ given by

$$x⪯y⟺x\ge y.$$

Consider the following mappings $\mathcal{T},\mathcal{S}:\mathcal{X}\to B(\mathcal{X})$:

$$\mathcal{T}x=[0.3x,0.5x],\mathcal{S}x=[0.2x,0.4x],x\in [0,+\mathrm{\infty }).$$

First, we check that $\mathcal{S}$ is $\mathcal{T}$-weakly isotone increasing. Suppose that $y\in \mathcal{S}x=[0.2x,0.4x]$ and $z\in \mathcal{S}x=[0.2x,0.4x]$. Then $u\in \mathcal{T}y$ implies that $u\le 0.5\cdot 0.4x=0.2x\le z$ and so $z⪯u$. This means that for any $x\in \mathcal{X}$, we have $\mathcal{S}x{⪯}_1\mathcal{T}y$ for all $y\in \mathcal{S}x$. Similarly, one can prove that for each $y\in \mathcal{S}x$, we have $\mathcal{T}y{⪯}_1\mathcal{S}z$ for all $z\in \mathcal{T}y$.

Let $\phi (t)=\frac{5}{7}t$ for $t\in [0,+\mathrm{\infty })$ and $L=1$. Now, we check that the condition (3.1) holds for all $x,y\in \mathcal{X}$. Consider the following two possibilities.

• 1. $x⪯y$, i.e., $x\ge y$. Denote $y=tx$, $0\le t\le 1$. Then

  

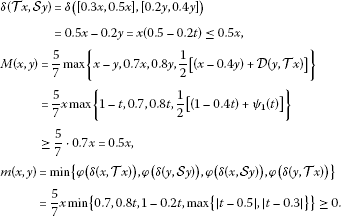
Hence, the condition (3.1) is satisfied.

• 2. $x\succ y$, i.e., $x<y$ and $x=ty$ for some $t\in (0,1)$. Then

  

Again, the condition (3.1) is satisfied. Thus, all the conditions of Theorem 3.1 are fulfilled, and $\mathcal{T}$ and $\mathcal{S}$ have an endpoint ($z=0$).

Similar corollaries can be obtained as in the previous section. For example, putting $\mathcal{S}=\mathcal{T}$ in Theorem 3.1, we obtain immediately the following result.

Corollary 3.4 Let $(\mathcal{X},d,⪯)$ be a complete partially ordered metric space. Assume that there is a continuous function $\phi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ with $\phi (t)<t$ for each $t>0$, $\phi (0)=0$ and that $\mathcal{T}:\mathcal{X}\to \mathcal{B}(\mathcal{X})$ is a multivalued mapping such that

$$\delta (\mathcal{T}x,\mathcal{T}y)\le M(x,y)+Lmin\{\phi (\delta (x,\mathcal{T}x)),\phi (\delta (y,\mathcal{T}y)),\phi (\delta (x,\mathcal{T}y)),\phi (\delta (y,\mathcal{T}x))\}$$

for all comparable $x,y\in \mathcal{X}$, where $L\ge 0$, and

$$M(x,y)=max\{\phi (d(x,y)),\phi (\delta (x,\mathcal{T}x)),\phi (\delta (y,\mathcal{T}y)),\phi \left(\frac{\mathcal{D}(x,\mathcal{T}y)+\mathcal{D}(y,\mathcal{T}x)}{2}\right)\}.$$

Also, suppose that $\mathcal{T}x{⪯}_1\mathcal{T}(\mathcal{T}x)$ for all $x\in \mathcal{X}$ and that there is $x_0\in \mathcal{X}$ such that $\{x_0\}{\prec }_1\mathcal{T}{x}_0$. If the condition (2.3) holds, then $\mathcal{T}$ has an endpoint.

To conclude this section, we provide a sufficient condition to ensure the uniqueness of the endpoint in Theorem 3.1,

Theorem 3.5 Adding to the hypotheses of Theorem  3.1 the condition

$$\underset{n\to \mathrm{\infty }}{lim}diam({(\mathcal{T}\circ \mathcal{S})}^n(\mathcal{X}))=0,$$

where ∘ denotes the composition of mappings, we obtain the uniqueness of the common endpoint of $\mathcal{S}$ and $\mathcal{T}$.

Proof Let z and $z^{\prime }$ be two common fixed points of $\mathcal{S}$ and $\mathcal{T}$, that is,

$$z\in \mathcal{T}z\cap \mathcal{S}z\text{and}{z}^{\prime }\in \mathcal{T}{z}^{\prime }\cap \mathcal{S}{z}^{\prime }.$$

It is immediate to show that for all $n\in \mathbb{N}$, we have

$${(\mathcal{T}\circ \mathcal{S})}^{n}x=x,\text{for all }x\in \{z,z^{\prime }\}.$$

Then

$$d(z,z^{\prime })=\delta ({(\mathcal{T}\circ \mathcal{S})}^{n}z,{(\mathcal{T}\circ \mathcal{S})}^n{z}^{\prime })\le diam({(\mathcal{T}\circ \mathcal{S})}^n(\mathcal{X}))\to 0\text{as }n\to \mathrm{\infty }.$$

Hence, $z=z^{\prime }$ and the proof is completed. □