- Research
- Open access
- Published:
Stability results in non-Archimedean -fuzzy normed spaces for a cubic functional equation
Journal of Inequalities and Applications volume 2012, Article number: 193 (2012)
Abstract
We establish some stability results concerning the functional equation
where is a fixed integer in the setting of non-Archimedean -fuzzy normed spaces.
MSC:39B52, 46S10, 46S40, 47S10, 47S40.
1 Introduction
The theory of fuzzy sets was introduced by Zadeh [34] in 1965. After the pioneering work of Zadeh, there has been a great effort to obtain fuzzy analogues of classical theories. Among other fields, a progressive development has been made in the field of fuzzy topology [1, 8, 9, 12–14, 18, 22, 30]. One of the problems in -fuzzy topology is to obtain an appropriate concept of -fuzzy metric spaces and -fuzzy normed spaces. In 2004, Park [23] introduced and studied the notion of intuitionistic fuzzy metric spaces. In 2006, Saadati and Park [28] introduced and studied the notion of intuitionistic fuzzy normed spaces.
On the other hand, the study of stability problems for a functional equation is related to the question of Ulam [33] concerning the stability of group homomorphisms and affirmatively answered for Banach spaces by Hyers [19]. Subsequently, the result of Hyers was generalized by Aoki [2] for additive mappings and by Rassias [24] for linear mappings by considering an unbounded Cauchy difference. We refer the interested readers for more information on such problems to the papers [4, 6, 11, 20, 21, 25, 29, 32, 33].
Let X and Y be real linear spaces and a mapping. If , the cubic function , where c is a real constant, clearly satisfies the functional equation
Hence, the above equation is called the cubic functional equation. Recently, Cho, Saadati and Wang [5] introduced the functional equation
which has () as a solution for .
In this paper, we investigate the Hyers-Ulam stability of the functional equation as follows:
where is a fixed integer.
2 Preliminaries
In this section, we recall some definitions and results for our main result in this paper.
A triangular norm (shorter t-norm) is a binary operation on the unit interval , i.e., a function satisfying the following four axioms: for all ,
-
(i)
(commutativity);
-
(ii)
(associativity);
-
(iii)
(boundary condition);
-
(iv)
whenever (monotonicity).
Basic examples are the Łukasiewicz t-norm and the t-norms , and , where , , and
for all .
For all and all t-norms T, let . For all and all t-norms T, define by the recursion equation for all . A t-norm T is said to be Hadžić type (we denote it by ) if the family is equicontinuous at (see [15]).
Other important triangular norms are as follows (see [16]):
-
The Sugeno-Weber family is defined by , and
if .
-
The Domby family is defined by , if , , if and
if .
-
The Aczel-Alsina family is defined by , if , , if and
if .
A t-norm T can be extended (by associativity) in a unique way to an r-array operation by taking, for any , the value defined by
A t-norm T can also be extended to a countable operation by taking, for any sequence in , the value
The limit on the right side of (2.1) exists since the sequence is non-increasing and bounded below.
Proposition 2.1 [16]
-
(1)
For , the following equivalence holds:
-
(2)
If T is of Hadžić type, then
for all sequence in such that .
-
(3)
If , then
-
(4)
If , then
3 -fuzzy normed spaces
In this section, we give some definitions and related lemmas for our main result.
Definition 3.1 [10]
Let be a complete lattice and U a non-empty set called a universe. An -fuzzy set on U is defined by a mapping . For any , represents the degree (in L) to which u satisfies .
Lemma 3.2 [7]
Consider the set and the operation defined by

for all . Then is a complete lattice.
Definition 3.3 [3]
An intuitionistic fuzzy set on a universe U is an object , where and for all are called the membership degree and the non-membership degree, respectively, of u in , and furthermore, they satisfy .
In Section 2, we presented the classical definition of t-norms, which can be straight-forwardly extended to any lattice . Define first and .
Definition 3.4 A triangular norm (t-norm) on is a mapping satisfying the following conditions:
-
(i)
for all (boundary condition);
-
(ii)
for all (commutativity);
-
(iii)
for all (associativity);
-
(iv)
and for all (monotonicity).
A t-norm can also be defined recursively as an -array operation for each by and
for all and .
The t-norm defined by
is a continuous t-norm.
Definition 3.5 A t-norm on is said to be t-representable if there exist a t-norm T and a t-conorm S on such that
for all , .
Definition 3.6
-
(1)
A negator on is any decreasing mapping satisfying and .
-
(2)
If a negator on satisfies for all , then is called an involution negator.
-
(3)
The negator on defined as for all is called the standard negator on .
Definition 3.7 The 3-tuple is said to be an -fuzzy normed space if V is a vector space, is a continuous t-norm on and is an -fuzzy set on satisfying the following conditions: for all and ,
-
(a)
;
-
(b)
;
-
(c)
for all ;
-
(d)
;
-
(e)
is continuous;
-
(f)
and .
In this case, is called an -fuzzy norm. If is an intuitionistic fuzzy set and the t-norm is t-representable, then the 3-tuple is said to be an intuitionistic fuzzy normed space.
Definition 3.8 (see [27])
Let be an -fuzzy normed space.
-
(1)
A sequence in is called a Cauchy sequence if, for any and for any , there exists a positive integer such that
for all and , where is a negator on .
-
(2)
A sequence in is said to be convergent to a point in the -fuzzy normed space (denoted by\hspace*{-6pt}
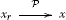 \hspace*{-6pt}) if wherever for all .
\hspace*{-6pt}) if wherever for all . -
(3)
If every Cauchy sequence in is convergent in V, then the -fuzzy normed space is said to be complete and the -fuzzy normed space is called an -fuzzy Banach space.
Lemma 3.9 [26]
Let be an -fuzzy norm on V. Then we have the following:
-
(1)
is non-decreasing with respect to for all x in V.
-
(2)
for all x, y in V and all .
Definition 3.10 Let be an -fuzzy normed space. For any , we define the open ball with center and radius as
A subset is called open if, for all , there exist and such that .
Let denote the family of all open subsets of V. Then is called the topology induced by the -fuzzy norm .
4 -fuzzy Hyers-Ulam stability for cubic functional equations in non-Archimedean -fuzzy normed spaces
In 1897, Hensel [17] introduced the field with valuation in which does not have the Archimedean property.
Definition 4.1 Let be a field. A non-Archimedean absolute value on is a function such that, for any ,
-
(1)
and equality holds if and only if ,
-
(2)
,
-
(3)
(the strict triangle inequality).
Note that for each integer n. We always assume, in addition, that is non-trivial, i.e., there is such that .
Definition 4.2 A non-Archimedean -fuzzy normed space is a triple , where V is a vector space, is a continuous t-norm on and is an -fuzzy set on satisfying the following conditions: for all and ,
-
(a)
;
-
(b)
;
-
(c)
for all ;
-
(d)
;
-
(e)
is continuous;
-
(f)
and .
From now on, let be a non-Archimedean field, X a vector space over and a non-Archimedean -fuzzy Banach space over . We investigate the Hyers-Ulam stability of the cubic functional equation (1.1).
Next, we define an -fuzzy approximately cubic mapping. Let Ψ be an -fuzzy set on such that is non-decreasing,
and
for all , all and all .
Definition 4.3 A mapping is said to be Ψ-approximately cubic if

for all and all .
The following is the main result in this paper.
Theorem 4.4 Let be a Ψ-approximately cubic mapping. If and there are and an integer k () with such that
and
for all and all , then there exists a unique cubic mapping such that
for all and all , where
for all and all .
Proof Let be the identity mapping . First, we show, by induction on j, that
for all , all and all . Putting in (4.1), we obtain
for all and all . This proves (4.4) for . Let (4.4) hold for some . Replacing y by 0 and x by in (4.1), we get
for all and all . Since , it follows that

for all and all . Thus (4.4) holds for all . In particular, we have
for all and all . Replacing x by in the above inequality and using the inequality (4.2), we obtain
for all , all and all , and so

for all , all and all . Hence it follows that

for all , all and all . Since for all and all , is a Cauchy sequence in the non-Archimedean -fuzzy Banach space . Hence we can define a mapping such that
for all and all . Next, for all , all and all , we have
for all and all , and so
for all and all . Taking the limit as in the above inequality, we obtain
for all and all , which proves (4.3).
Since is continuous, from the well-known result in an -fuzzy (probabilistic) normed space (see [31], Chapter 12), it follows that

for all and all . On the other hand, replacing x, y by , in (4.1) and (4.2), we get

for all and all . Since , we infer that C is a cubic mapping.
For the uniqueness of C, let be another cubic mapping such that
for all and all . Then we have, for all and all ,

Therefore, from (4.5), we conclude that . This completes the proof. □
Corollary 4.5 Let and let be a Ψ-approximately cubic mapping. If and there are and an integer k () with such that
and
for all and all , then there exists a unique cubic mapping such that
for all and all , where
for all and all .
Proof Since
for all and all and is of type, it follows from Proposition 2.1 that
for all and all . Therefore, if we apply Theorem 4.4, then we get the conclusion. This completes the proof. □
Example 4.6 Let be a non-Archimedean Banach space, a non-Archimedean -fuzzy normed space (intuitionistic fuzzy normed space) in which
for all and all and a complete non-Archimedean -fuzzy normed space (intuitionistic fuzzy normed space). Define
for all and all . It is easy to see that (4.2) holds for . Also, since
for all and all , we have
for all and all . Let be a Ψ-approximately cubic mapping. A straightforward computation shows that

for all and all . Therefore, all the conditions of Theorem 4.4 hold, and so there exists a unique cubic mapping such that
for all and all .
References
Amini M, Saadati R: Topics in fuzzy metric space. J. Fuzzy Math. 2003, 4: 765–768.
Aoki T: On the stability of the linear transformation in Banach spaces. J. Math. Soc. Jpn. 1950, 2: 64–66. 10.2969/jmsj/00210064
Atanassov KT: Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20: 87–96. 10.1016/S0165-0114(86)80034-3
Baak C, Moslehian MS:On the stability of -homomorphisms. Nonlinear Anal., Theory Methods Appl. 2005, 63: 42–48. 10.1016/j.na.2005.04.004
Cho, YJ, Saadati, R, Wang, S: Nonlinear $\mathcal{L}$L-fuzzy stability of functional equations. Preprint
Czerwik S: Functional Equations and Inequalities in Several Variables. World Scientific, River Edge; 2002.
Deschrijver G, Kerre EE: On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst. 2003, 123: 227–235.
George A, Veeramani P: On some result in fuzzy metric space. Fuzzy Sets Syst. 1994, 64: 395–399. 10.1016/0165-0114(94)90162-7
George A, Veeramani P: On some result of analysis for fuzzy metric spaces. Fuzzy Sets Syst. 1997, 90: 365–368. 10.1016/S0165-0114(96)00207-2
Goguen J:-fuzzy sets. J. Math. Anal. Appl. 1967, 18: 145–174. 10.1016/0022-247X(67)90189-8
Gordji ME, Ghaemi MB, Hajani H: Generalized Hyers-Ulam-Rassias theorem in Menger probabilistic normed spaces. Discrete Dyn. Nat. Soc. 2010., 2010: Article ID 162371
Gregory V, Romaguera S: Some properties of fuzzy metric spaces. Fuzzy Sets Syst. 2000, 115: 485–489. 10.1016/S0165-0114(98)00281-4
Gregory V, Romaguera S: On completion of fuzzy metric spaces. Fuzzy Sets Syst. 2002, 130: 399–404. 10.1016/S0165-0114(02)00115-X
Gregory V, Romaguera S: Characterizing completable fuzzy metric spaces. Fuzzy Sets Syst. 2004, 144: 411–420. 10.1016/S0165-0114(03)00161-1
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces. Kluwer Academic, Dordrecht; 2001.
Hadžić O, Pap E, Budincević M: Countable extension of triangular norms and their applications to the fixed point theory in probabilistic metric spaces. Kybernetika 2002, 38: 363–381.
Hensel K: Über eine neue Begrüngdung der Theorie der algebraishen Zahlen. Jahresber. Dtsch. Math.-Ver. 1897, 6: 83–88.
Hu C:-structure of FTS. V: fuzzy metric spaces. J. Fuzzy Math. 1995, 3: 711–721.
Hyers DH: On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27: 222–224. 10.1073/pnas.27.4.222
Hyers DH, Isac G, Rassias TM: Stability of Functional Equations in Several Variables. Birkhäuser, Basel; 1998.
Jung S: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor; 2001.
Lowen R: Fuzzy Set Theory. Kluwer Academic, Dordrecht; 1996.
Park J: Intuitionistic fuzzy metric spaces. Chaos Solitons Fractals 2004, 22: 1039–1046. 10.1016/j.chaos.2004.02.051
Rassias TM: On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 1978, 72: 297–300. 10.1090/S0002-9939-1978-0507327-1
Rassias TM: Functional Equations, Inequalities and Applications. Kluwer Academic, Dordrecht; 2003.
Saadati R: A note on “Some results on the IF-normed spaces”. Chaos Solitons Fractals 2009, 41: 206–213. 10.1016/j.chaos.2007.11.027
Saadati R, Park C:Non-Archimedean -fuzzy normed spaces and stability of functional equations. Comput. Math. Appl. 2010, 60: 2488–2496. 10.1016/j.camwa.2010.08.055
Saadati R, Park J: On the intuitionistic fuzzy topological spaces. Chaos Solitons Fractals 2006, 27: 331–344. 10.1016/j.chaos.2005.03.019
Saadati R, Razani A, Adibi H:A common fixed point theorem in -fuzzy metric spaces. Chaos Solitons Fractals 2007, 33: 358–363. 10.1016/j.chaos.2006.01.023
Schweizer B, Sklar A: Statistical metric spaces. Pac. J. Math. 1960, 10: 314–334.
Schweizer B, Sklar A: Probabilistic Metric Spaces. North Holand, New York; 1983.
Shakeri S, Saadati R, Park C:Stability of the quadratic functional equation in non-Archimedean-fuzzy normed spaces. Int. J. Nonlinear Anal. Appl. 2010, 1: 72–83.
Ulam SM Science Editions. In Problems in Modern Mathematics. Wiley, New York; 1964. Chapter VI
Zadeh LA: Fuzzy sets. Inf. Control 1965, 8: 338–353. 10.1016/S0019-9958(65)90241-X
Acknowledgements
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (Grant number 2012003499).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment, and read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bae, JH., Lee, SB. & Park, WG. Stability results in non-Archimedean -fuzzy normed spaces for a cubic functional equation. J Inequal Appl 2012, 193 (2012). https://doi.org/10.1186/1029-242X-2012-193
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-193
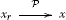 \hspace*{-6pt}) if wherever for all .
\hspace*{-6pt}) if wherever for all .