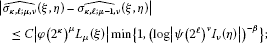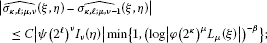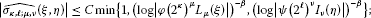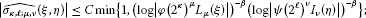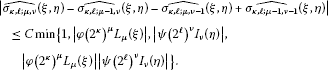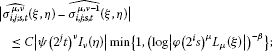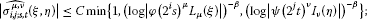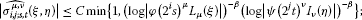- Research
- Open access
- Published:
Multiple singular integrals and Marcinkiewicz integrals with mixed homogeneity along surfaces
Journal of Inequalities and Applications volume 2012, Article number: 189 (2012)
Abstract
This paper is devoted to studying the singular integrals and Marcinkiewicz integrals with mixed homogeneity along surfaces, which contain many classical surfaces as model examples, on the product domains (). Under rather weak size conditions of the kernels, the -boundedness for such operators is established. These results essentially extend certain previous results.
MSC:42B20, 42B25.
1 Introduction
Let (), , be the d-dimensional Euclidean space and be the unit sphere in equipped with the induced Lebesgue measure . Let be fixed real numbers, (). Define the function by , . It is clear that for each fixed , the function is a decreasing function in . We let denote the unique solution of the equation . Fabes and Riviére [13] showed that is a metric space, which is often called the mixed homogeneity space related to . For , we let be the diagonal matrix . Let , we denote by for , where .
Let , . It is easy to check that

The change of variables related to the spaces is given by the transformation

Thus , where is the Jacobian of the above transform and , . Obviously, and there exists such that
Let and satisfy the following conditions:

Define the parabolic singular integral operator T by
As is well known, a singular integral operator of the type (1.1) originally arose from the study on the existence and regularity results of the heat equation and the more general parabolic differential operator with constant coefficients. In 1966, Fabes and Riviére [13] showed that T is bounded on for if . Subsequently, Nagel, Riviére and Wainger [18] weakened the regularity condition on Ω to the case . Recently, Chen, Ding and Fan [5] extended further the condition to the case .
In this paper, we will continue the research along this line. We will focus our attention on the multiple singular integrals with mixed homogeneity. Assume that and satisfies the following conditions:


We consider the multiple singular integral with mixed homogeneity defined by
In 2011, Chen and Le [8] showed that if , then is bounded on for . On the other hand, in the special case (; ), is the classical multiple singular integral, which is studied extensively by many authors (see [2, 10, 12, 14, 15, 19, 25, 27, 28] for examples). In particular, Ying [28] (also see [27] for a more general case) proved that is bounded on for and provided that Ω satisfies the following condition:
where
It should be pointed out that the condition (1.5) for one parameter case was originally defined in Walsh’s paper [22] and developed by Grafakos and Stefanov [16]. For the sake of simplicity, we denote that for ,
Employing the ideas in [16], one easily verifies that for , and
Based on the above, a natural question is as follows.
Question 1.1 For the general case () and (), is bounded on under the condition (1.5) for some ?
One of the main purposes of this paper is to give a positive answer to the above question. The method we use allows us to treat a family of operators broader than those given by (1.4). To be precise, for suitable functions and two real polynomial on with and for , where is the degree of (), we define the multiple singular integral operator along surfaces by

where
Obviously, is the special case of for (). Also, in the special case (; ),
Moreover, for the special case and (; ),
Wu and Yang [27] proved that if with , then is bounded on for . In this paper, we will extend the result above as follows.
Theorem 1.1 Let and be two real polynomials on with and for , where is the degree of (), and let , where is the set of functions ϕ satisfying the following properties:
-
(i)
is continuous strictly increasing and satisfying that is monotonous;
-
(ii)
there exist constants such that and for all .
Suppose that Ω satisfies (1.2)-(1.3) and for some . Then defined as in (1.7) is bounded on for . The bound is independent of the coefficients of (), but depends on φ, ψ, , , m, n and β.
Remark 1.1 For any , there exists a constant such that for all . To see this, by the mean-valued theorem, for any , there exists such that . The properties (i) and (ii) of ϕ imply that
Taking , this is the desired constant.
Remark 1.2 We remark that the model examples for functions are (), , and real-valued polynomials P on with positive coefficients and (see [3]). Theorem 1.1 extends the result of [27], which is the multiple-parameter generalization of the result in [11, 16], to the mixed homogeneity setting, even in the special case . Also, by (1.6), Theorem 1.1 is distinct from the result of [8], even in the special case .
On the other hand, we also consider the multiple Marcinkiewicz integral operator along the surfaces defined by
where
and .
When , (; ), we denote by , which is the classical Marcinkiewicz integral on the product domains and is studied extensively by many authors (see [1, 3, 4, 6, 7, 17, 23–26]et al.). In particular, Al-Qassem, Al-Salman, Cheng and Pan [1] showed that if , then is bounded on for ; Hu, Lu and Yan [17] (also see [23, 26]) proved that if for , then is bounded on for . For the general operator , when () and , Al-Salman [3] showed that is bounded on for provided that .
A natural question which arises from the above is the following:
Question 1.2 Under the condition (1.5) with , is also bounded on for ?
This question will be addressed by our next theorem.
Theorem 1.2 Let (), φ, ψ be as in Theorem 1.1. Suppose for some and satisfies (1.2)-(1.3). Then defined as (1.9) is bounded on for . The bound is independent of the coefficients of () but depends on φ, ψ, , , m, n and β.
Remark 1.3 Theorem 1.2 extends the result of [17] to the mixed homogeneity setting, even for the special case . And by (1.6), Theorem 1.2 is distinct from the result of [3], even in the special case .
The rest of this paper is organized as follows. After recalling some notation and establishing some preliminary lemmas, we will prove Theorem 1.1 in Section 2. And the proof of Theorem 1.2 will be given in Section 3. We remark that our some ideas in the proofs of our main results are taken from [3, 9, 11, 17], but our methods and technique are more delicate and complex than those used in [3, 9, 11, 17].
Throughout this paper, the letter C or c, sometimes with additional parameters, will stand for positive constants, not necessarily the same at each occurrence but independent of the essential variables.
2 On multiple singular integrals
Let us begin with some notations and lemmas. For given positive polynomials , and two smooth functions , we set

Then for ; ,

We denote , and set whenever ; whenever . So we can write
where . Similarly,
where . For , , we set

Here we use the convention . Hence,

For any and , , we define the measures and as follows.
where . By (1.3) and , , for and we have
Then it is easy to see that
Lemma 2.1 (cf. [21], pp.476-478])
Let be a polynomial mapping , where and is a real polynomial defined on (). Then the maximal function defined by
is bounded on for . The bound is independent of the coefficients of () and f.
Lemma 2.2 Let be a polynomial mapping , where and is a real polynomial defined on (). Suppose that . Then the operator defined by
is bounded on for . The bound is independent of the coefficients of () and f, but depends on ϕ.
Proof For any , by the change of variable, it can be easily seen that

This implies that . Then Lemma 2.2 follows from Lemma 2.1. □
Lemma 2.3 Let . Suppose that and satisfies (1.2)-(1.3). Then, for , , the maximal operator defined by
is bounded on for . The bound is independent of the coefficients of () and f, but depends on φ, ψ, , , m, n.
Proof By the definition of , we have

where
By Lemma 2.2, using iterated integration, it is easy to see that
where C is independent of , . Thus
which completes the proof of Lemma 2.3. □
Lemma 2.4 (cf. [20], p.186, Corollary])
Let and , where are real parameters, and are distinct positive (not necessarily integer) exponents. Then
with and C does not depend on as long as .
Lemma 2.5 Suppose that . Then for any and , there exist and such that for any

The constant is independent of the coefficients of but depends on φ; and is independent of the coefficients of but depends on ψ.
Proof We only prove the first inequality, since a similar argument can get the second inequality. By the change of variables, we have

where , , . Let
By Lemma 2.4, there exists such that
Thus by integration by parts and the fact that is monotonous, we have

Using , we get
This proves Lemma 2.5. □
Lemma 2.6 Let . Suppose that for some and satisfies (1.2)-(1.3). Then for and , there exists a constant such that
-
(i)
if , then
 (2.5)
(2.5) -
(ii)
if , then
 (2.6)
(2.6) -
(iii)
if and , then
 (2.7)
(2.7)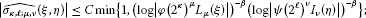 (2.8)
(2.8)(iv)
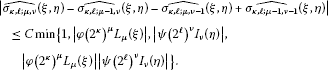 (2.9)
(2.9)
The constant C is independent of the coefficients of and .
Proof Let

By Lemma 2.5, there exist such that

When , since is increasing in , we have
Then
Similarly, when ,
By the definition of , we have

Combining (2.11) with the fact , we obtain (2.5). Similarly, we can conclude (2.6). To prove (2.7) and (2.8), we write
Then (2.7) and (2.8) follow from (2.10)-(2.11) with the fact . Finally, (2.9) follows from the inequality

This completes the proof of Lemma 2.6. □
Now we take two radial Schwartz functions and such that for and for (), where , are as in Remark 1.1. Define the measures by
for , and , where we use the convention . By (2.3), it is easy to see that
Lemma 2.7 Let Ω, φ, ψ be as in Lemma 2.6. For and , , we have (i)
-
(ii)
if , then
(2.14) -
(iii)
if , then
(2.15) -
(iv)
if and , then
(2.16)
Here and below, () is as in Remark 1.1, the constant C is independent of the coefficients of ().
Proof We write , . Then
Thus, it is easy to see that
Notice that


Invoking Lemma 2.6, we get (2.13). On the other hand, since


by (2.17) and (2.20), we have
Then (2.14) follows from (2.6)-(2.7) with (2.19). Similarly, we get (2.15). Finally, (2.16) follows from (2.8), (2.17), (2.20) and (2.21). This completes the proof of Lemma 2.7. □
By Lemma 2.3 and the definition of , it is easy to verify the following lemma.
Lemma 2.8 Let be as in Lemma 2.3. Then for and , we have
for . The constant C is independent of the coefficients of and .
Applying Lemma 2.8 and [9], p.544, Lemma], we can obtain
Lemma 2.9 Let Ω, φ, ψ be as in Lemma 2.3. Then for and , we have
for and any arbitrary functions . The constant C is independent of the coefficients of and .
Now we are in the position of proving Theorem 1.1.
Proof of Theorem 1.1 Combining (2.4) with (2.12), we write
It suffices to show that for and ,
For fixed and , choose two collections of functions and on with the following properties:
-
(i)
, ;
-
(ii)
, , ;
-
(iii)
, where C is a constant.
Define the multiplier operator on by
Then
Now we consider the -boundedness of . By the Littlewood-Paley theory and Lemma 2.9, we have
On the other hand, by the Littlewood-Paley theory and Plancherel’s theorem, we have
where . Using Lemma 2.7 and Remark 1.1, we have
where
Interpolating (2.26) and (2.27), for any , we can obtain such that and
Then we have
This together with (2.22) and (2.25) completes the proof of Theorem 1.1. □
3 On the multiple Marcinkiewicz integrals
This section is devoted to the proof of Theorem 1.2. We first introduce some notations and lemmas. For , and , , we define the measures and by


where and , were defined as in Section 2. It is obvious that for ,
and
Lemma 3.1 Let , and . Suppose that for some and satisfies (1.2)-(1.3). Then for each pair μ and ν, there exists a constant such that
-
(i)
if , then
 (3.4)
(3.4) -
(ii)
if , then
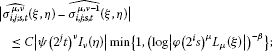 (3.5)
(3.5) -
(iii)
if and , then
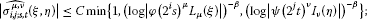 (3.6)
(3.6)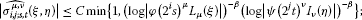 (3.7)
(3.7)(iv)
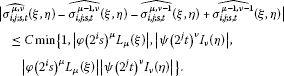 (3.8)
(3.8)
The constant C is independent of the coefficients of and .
Proof Set

By Lemma 2.5, there exist such that


When , since is increasing in , we have
Similarly, when
By the definition of , we have

Combining (3.12) with the fact , we obtain (3.4). Similarly, we can conclude (3.5). To prove (3.6) and (3.7), we write
Combining (3.11)-(3.12) with the fact that , we get (3.6) and (3.7). Finally, (3.8) follows from the inequality

This completes the proof of Lemma 3.1. □
We now take two radial Schwartz functions and such that for and for (), where , are as in Remark 1.1. Define the measures by
where , , for , , , . Here we use the convention . It is easy to see that
Applying Lemma 3.1 and the same arguments as in proving Lemma 2.7, we have
Lemma 3.2 Let Ω, φ, ψ be as in Lemma 3.1. Then for and , ; , there exists a constant such that
-
(i)
;
-
(ii)
if , then
-
(iii)
if , then
-
(iv)
if and , then
Here the constant C is independent of the coefficients of ().
By Lemma 2.2 and the same arguments as in proving Lemma 2.3, we have the following lemma:
Lemma 3.3 Let . Suppose that and satisfies (1.2)-(1.3). Then for , , the maximal operator
is bounded on for . The bound is independent of the coefficients of () but depends on φ, ψ, , , m, n.
Applying Lemma 3.3, we have
Lemma 3.4 Let Ω, φ, ψ be as in Lemma 3.3. Then for and ,
The constant C is independent of the coefficients of ().
Furthermore, applying Lemma 3.4 and [9], p.544, Lemma], we can obtain
Lemma 3.5 Let Ω, φ, ψ be as in Lemma 3.3. For ; , and any arbitrary functions , then

where the constant C is independent of the coefficients of ().
Lemma 3.6 Let Ω, φ, ψ be as in Lemma 3.3. Then for and , there exists a constant such that for

where are arbitrary functions defined on . The constant is independent of the coefficients of ().
Proof We consider the mapping . By Lemma 3.4, we have for
which implies .
On the other hand. By the dual argument and Lemma 3.4, we have
which implies . Then Lemma 3.6 follows from the standard interpolation arguments. □
Lemma 3.7 Let be the multiplier operators defined in (2.24) for any . Then (i) for each fixed and for any functions

(ii) for each fixed and for any functions ,

By the arguments similar to those used in [17], pp.78-81], we easily establish this lemma. The details are omitted.
Now we turn to prove Theorem 1.2.
Proof of Theorem 1.2 By (3.3) and (3.13), we can write
It suffices to show that is bounded on for and . By the definitions of , we can write
Case 1. . Combining with (3.17) and Lemma 3.7, we know that for
For fixed , let
By Lemma 3.6 and the Littlewood-Paley theory, we have
On the other hand, by Plancherel’s theorem and Lemma 3.2, we know that
where is as in the proof of Theorem 1.1. Then
where is as in (2.28). Interpolating between (3.19) and (3.20), there exists such that
For fixed , we can choose such that . Then
which implies
Case 2. . By (3.17) and Lemma 3.7, we have, for and any ,
Let
By Lemma 3.5 and the Littlewood-Paley theory, we have that for and ,
On the other hand, by the same argument as in getting (3.20), we have
where is as in (2.28). By interpolating between (3.23) and (3.24), for fixed , we can choose and such that and
Combining this with (3.22), we have
This together with (3.21) completes the proof of Theorem 1.2. □
References
Al-Qassem H, Al-Salman A, Cheng L, Pan Y: Marcinkiewicz integrals on product spaces. Stud. Math. 2005, 167: 227–234. 10.4064/sm167-3-4
Al-Salman A, Al-Qassem H, Pan Y: Singular integrals on product domains. Indiana Univ. Math. J. 2006, 55(1):369–387. 10.1512/iumj.2006.55.2626
Al-Salman A: Parabolic Marcinkiewicz integrals along surfaces on product domains. Acta Math. Sin. Engl. Ser. 2011, 27(1):1–18.
Chen J, Ding Y, Fan D: Certain square functions on product spaces. Math. Nachr. 2001, 230: 5–18. 10.1002/1522-2616(200110)230:1<5::AID-MANA5>3.0.CO;2-O
Chen Y, Ding Y, Fan D: A parabolic singular integral operator with rough kernel. J. Aust. Math. Soc. 2008, 84: 163–179.
Chen J, Fan D, Ying Y: The method of rotation and Marcinkiewicz integrals on product domains. Stud. Math. 2002, 153(1):41–58. 10.4064/sm153-1-4
Choi Y: Marcinkiewicz integrals with rough homogeneous kernel of degree zero on product domains. J. Math. Anal. Appl. 2001, 261: 53–60. 10.1006/jmaa.2001.7465
Chen L, Le H: Singular integrals with mixed homogeneity in product spaces. Math. Inequal. Appl. 2011, 14(1):155–172.
Duoandikoetxea J, Rubio de Francia JL: Maximal and singular integral operators via Fourier transform estimates. Invent. Math. 1986, 84: 541–561. 10.1007/BF01388746
Duoandikoetxea J: Multiple singular integrals and maximal functions along hypersurfaces. Ann. Inst. Fourier 1986, 36(4):185–206. 10.5802/aif.1073
Fan D, Guo K, Pan Y: A note of a rough singular integral operator. Math. Inequal. Appl. 1999, 2(1):73–81.
Fan D, Guo K, Pan Y: Singular integrals with rough kernels on product spaces. Hokkaido Math. J. 1999, 28: 435–460.
Fabes E, Reviére N: Singular integrals with mixed homogeneity. Stud. Math. 1966, 27: 19–38.
Fefferman R: Singular integrals on product domains. Bull. Am. Math. Soc. 1981, 4: 195–201. 10.1090/S0273-0979-1981-14883-7
Fefferman F, Stein EM: Singular integrals on product domains. Adv. Math. 1982, 45: 117–143. 10.1016/S0001-8708(82)80001-7
Grafakos L, Stefanov A: bounds for singular integrals and maximal singular integrals with rough kernels. Indiana Univ. Math. J. 1998, 47: 455–469.
Hu G, Lu S, Yan D: boundedness for the Marcinkiewicz integrals on product spaces. Sci. China Ser. A 2003, 46(1):75–82. 10.1360/03ys9008
Nagel A, Riviére NM, Wainger S: On Hilbert transforms along curves, II. Am. J. Math. 1976, 98: 395–403. 10.2307/2373893
Ricci F, Stein EM: Multiparameter singular integrals and maximal functions. Ann. Inst. Fourier 1992, 42: 637–670. 10.5802/aif.1304
Ricci R, Stein EM: Harmonic analysis on nilpotent groups and singular integrals I: oscillatory integrals. J. Funct. Anal. 1987, 73: 179–184. 10.1016/0022-1236(87)90064-4
Stein EM: Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton University Press, Princeton; 1993.
Walsh T: On the function of Marcinkiewicz. Stud. Math. 1972, 44: 203–217.
Wu H: Boundedness of multiple Marcinkiewicz integral operators with rough kernels. J. Korean Math. Soc. 2006, 43(3):635–658.
Wu H: A rough multiple Marcinkiewicz integral along continuous surfaces. Tohoku Math. J. 2007, 59(2):145–166. 10.2748/tmj/1182180732
Wu H: General Littlewood-Paley functions and singular integral operators on product spaces. Math. Nachr. 2006, 279(4):431–444. 10.1002/mana.200310369
Wu H, Xu J: Rough Marcinkiewicz integrals associated to surfaces of revolution on product domains. Acta Math. Sci., Ser. B 2009, 29(2):294–304.
Wu H, Yang S: On multiple singular integrals along polynomial curves with rough kernels. Acta Math. Sin. Engl. Ser. 2008, 24(2):177–184.
Ying Y: A note on singular integral operators on product domains. J. Math. Study 1999, 32(3):264–271. in Chinese
Acknowledgements
The authors would like to thanks the referees for their carefully reading and invaluable comments. This work was Supported by the NNSF of China (11071200) and the NSF of Fujian Province of China (No. 2010J01013).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
Both authors worked jointly in drafting and approving the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, F., Wu, H. Multiple singular integrals and Marcinkiewicz integrals with mixed homogeneity along surfaces. J Inequal Appl 2012, 189 (2012). https://doi.org/10.1186/1029-242X-2012-189
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-189