- Research
- Open access
- Published:
On the generalized Hyers-Ulam-Rassias stability problem of radical functional equations
Journal of Inequalities and Applications volume 2012, Article number: 186 (2012)
Abstract
In this paper, the generalized Hyers-Ulam-Rassias stability problem of radical quadratic and radical quartic functional equations in quasi-β-Banach spaces and then the stability by using subadditive and subquadratic functions for radical functional equations in -Banach spaces are given.
MSC:39B82, 39B52, 46H25.
1 Introduction
In 1960, the stability problem of functional equations originated from the question of Ulam [1, 2] concerning the stability of group homomorphisms. The famous Ulam stability problem was partially solved by Hyers [3] in Banach spaces. Later, Aoki [4] and Bourgin [5] considered the stability problem with unbounded Cauchy differences. Rassias [6–9] provided a generalization of Hyers’ theorem by proving the existence of unique linear mappings near approximate additive mappings. On the other hand, Rassias [10, 11] considered the Cauchy difference controlled by a product of different powers of norm. The above results have been generalized by Forti [12] and Gǎvruta [13], who permitted the Cauchy difference to become arbitrary unbounded. Gajda and Ger [14] showed that one can get analogous stability results for subadditive multifunctions. Gruber [15] remarked that Ulam’s problem is of particular interest in probability theory and in the case of functional equations of different types. Recently, Baktash et al. [16], Cho et al. [17–20], Gordji et al. [21–24], Lee et al. [25, 26], Najati et al. [27, 28], Park et al. [29], Saadati et al. [30] and Savadkouhi et al. [31] have studied and generalized several stability problems of a large variety of functional equations.
The most famous functional equation is the Cauchy equation
any solution of which is called additive. It is easy to see that the function defined by , where c is an arbitrary constant, is a solution of the functional equation
Thus it is natural that each equation is said to be a quadratic functional equation. In particular, every solution of the quadratic equation (1.1) is said to be a quadratic function.
Lee et al. [32] considered the following functional equation:
The functional equation (1.2) clearly has as a solution when f is a real valued function of a real variable. So, it is said to be a quartic functional equation.
Before we present our results, we introduce here some basic facts concerning quasi-β-normed space and preliminary results. Let β be a real number with , and be either or . Let X be a linear space over . A quasi-β-norm is a real-valued function on X satisfying the following:
-
(1)
for all and if and only if ;
-
(2)
for all
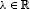 and ;
and ; -
(3)
There is a constant such that for all .
Then is called a quasi-β-normed space if is a quasi-β-norm on X. The smallest possible K is called the module of concavity of . A quasi-β-Banach space ia a complete quasi-β-normed space.
A quasi-β-norm is called a -norm if for all . In this case, a quasi-β-Banach space is called a -Banach space.
In [33], Tabor investigated a version of the Hyers-Rassias-Gajda theorem in quasi-Banach spaces. For further details on quasi-β normed spaces and -Banach space, we refer to the papers [34–37].
In this paper, we consider the following functional equations:


and discuss the generalized Hyers-Ulam-Rassias stability problem in quasi-β-normed spaces and then the stability by using subadditive and subquadratic functions for the functional equations (1.3) and (1.4) in -Banach spaces.
2 Stability of radical functional equations
Using an idea of Gǎvruta [13], we prove the generalized stability of (1.3) and (1.4) in the spirit of Ulam, Hyers and Rassias.
In [38], Khodaei et al. proved the following result:
Lemma 2.1 Let X be a real linear space and be a function. Then we have the following:
-
(1)
If f satisfies the functional equation (1.3), then f is quadratic.
-
(2)
If f satisfies the functional equation (1.4), then f is quartic.
Proof We will only prove (2). Letting in (1.4), we get . Setting in (1.4), we have
for all . If we compare (1.4) with (2.1), we obtain that for all . Letting in (1.4) and then using and the evenness of f, we have for all . Putting in (1.4) and using , we get for all . By induction, we lead to for all and . We obtain , and so for all and . So, we have
for all and all . Replacing x and y by and in (1.4) respectively, we obtain
for all . Setting in (1.4) and using the evenness of f, we get
for all . Putting in (2.3) and using (2.2), we get
for all . Setting in (1.4) and using (2.2), we get
for all . It follows from (2.2), (2.3), (2.4) and (2.6) that
for all . So it follows from (2.5) and (2.7) that f satisfies (1.2). Therefore, f is quartic. This completes the proof. □
Let be a quasi-β-Banach space with the quasi-β-norm and K be the modulus of concavity of . Let be functions. A function is said to be ϕ-approximatively radical quadratic if
and a function is said to be ψ-approximatively radical quartic if
for all .
Theorem 2.2 Let be a ϕ-approximatively radical quadratic function with . If a function satisfies
and for all , then the limit exists for all and a function is unique quadratic satisfying the functional equation (1.3) and the inequality
for all .
Proof Replacing x and y by and in (2.8) respectively, we get
for all . It follows from (2.8) and (2.11) that
for all . Setting in (2.12), it follows from that
and so
for all . For any integers m, k with ,
for all . Then a sequence is a Cauchy sequence in a quasi-β-Banach space and so it converges. We can define a function by for all . From (2.8), the following inequality holds:

for all . Then and, by Lemma 2.1, is a quadratic function. Taking the limit in (2.15) with , we find that a function satisfies (2.10) near the approximate function f of the functional equation (1.3).
Next, we assume that there exists another quadratic function which satisfies the functional equation (1.3) and (2.10). Since satisfies (1.3), it easy to show that for all and . Then we have
for all . Letting , we establish for all . This completes the proof. □
Theorem 2.3 Let be a ϕ-approximatively radical quadratic function. If a function satisfies
and for all , then the limit exists for all and a function is unique quadratic satisfying the functional equation (1.3) and the inequality
for all .
Proof If x is replaced by in the inequality (2.13), then the proof follows from the proof of Theorem 2.2. □
Corollary 2.4 Let and . If a function satisfies the following inequality:
for all , then there exists a unique quadratic function satisfying the functional equation (1.3) and the following inequality:
for all .
Corollary 2.5 Let and . If a function satisfies the following inequality:
for all , then there exists a unique quadratic function satisfying the functional equation (1.3) and the following inequality:
for all .
Now, we give an example to illustrate that the functional equation (1.3) is not stable for in a quasi-1-Banach space with .
Example 2.6 Let  be defined by
be defined by
Consider the function  by the formula
by the formula
for all  . It is clear that f is bounded by on
. It is clear that f is bounded by on  . We prove that
. We prove that
for all  . To see this, if or , then we have (2.16). Now suppose that . Then there exists a positive integer k such that
. To see this, if or , then we have (2.16). Now suppose that . Then there exists a positive integer k such that
so that , , for all . It follows from the definition of f and (2.17) that

for all  with . Thus, the condition (2.16) holds true.
with . Thus, the condition (2.16) holds true.
Next, we claim that the quadratic equation (1.3) is not stable for . Assume that there exist a quadratic function  and a positive constant μ such that for all
and a positive constant μ such that for all  . Then there exists a constant
. Then there exists a constant  such that for all
such that for all  . So we have
. So we have
for all  . But, we can choose a with . If , then for all . For this x, we obtain
. But, we can choose a with . If , then for all . For this x, we obtain
which contradicts (2.18). Therefore, the quadratic equation (1.3) is not stable for in Corollary 2.5.
Theorem 2.7 Let be a ψ-approximatively radical quartic function with . If the function satisfies
and for all , then the limit for all exists and a function is unique quartic satisfying the functional equation (1.4) and the inequality
for all .
Proof Replacing x and y by and in (2.9) respectively, we have
for all . Again, replacing x and y by and in (2.9) respectively, we get
for all . It follows from (2.20) and (2.21) that

for all . Setting in (2.22) and , we have
for all . Setting in (2.9), we have
for all . It follows from (2.23) and (2.24) that
for all . Since , it follows from (2.24) and (2.25) that
for all . Hence we have

for all and . Then a sequence is a Cauchy sequence in , and so it converges to a point in . We can define a function by for all . From (2.9), the following inequality holds:
for all . Then, we have , and by Lemma 2.1, is quartic. Taking the limit in (2.27) with , we obtain that a function satisfies (2.19) near the approximate function f of the functional equation (1.4). The remaining assertion is similar to the corresponding part of Theorem 2.2. This completes the proof. □
Corollary 2.8 If there exist and ; if a function satisfies the inequality
for all , then there exists a unique quartic function which satisfies (1.4) and the inequality
for all .
We recall that a subadditive function is a function having a domain A and a codomain that are both closed under addition with the following property:
for all . Also, a subquadratic function is a function with and the following property:
for all .
Let be fixed. If there exists a constant L with such that a function satisfies
for all , then we say that ϕ is contractively subadditive if and ϕ is expansively superadditive if . It follows by the last inequality that ϕ satisfies the following properties:
for all and .
Similarly, if there exists a constant L with such that a function with satisfies
for all , then we say that ψ is contractively subquadratic if and ψ is expansively superquadratic if . It follows from the last inequality that ψ satisfies the following properties:
for all and .
From now on, we establish the modified Hyers-Ulam-Rassias stability of the equations (1.3) and (1.4) in a -Banach space .
Theorem 2.9 Let be a ϕ-approximatively radical quadratic function with . Assume that the function ϕ is contractively subadditive with a constant L satisfying . Then there exists a unique quadratic function which satisfies (1.3) and the inequality
for all , where
Proof Using (2.13) in the proof of Theorem 2.2, we get
for all . Thus it follows from (2.29) that
for all and integers . Then a sequence is a Cauchy sequence in a -Banach space , and so we can define a function by for all . Then, we get

for all , and so, by Lemma 2.1, is a quadratic function. Taking in (2.30) with , we have
Next, we assume that there exists a quadratic function which satisfies the functional equation (1.3) and (2.28). Then we have
for all . Letting , we have the uniqueness of . This completes the proof. □
Theorem 2.10 Let be a ϕ-approximatively radical quadratic function with . Assume that the function ϕ is expansively superadditive with a constant L satisfying . Then there exists a unique quadratic function which satisfies (1.3) and the inequality
for all .
Proof From (2.29) in the proof of Theorem 2.9, we get
for all . For integers k, m with , we get
The remaining part follows as the proof of Theorem 2.9. This completes the proof. □
Theorem 2.11 Let be a ψ-approximatively radical quadratic function with . Assume that the function ψ is contractively subquadratic with a constant L satisfying . Then there exists a unique quartic function which satisfies (1.4) and the inequality
where
for all .
Proof Using (2.26) in the proof of Theorem 2.7, we get
for all . Then it follows from (2.32) that

for all and . Then is a Cauchy sequence in , and it converges to a point in . We can define a function by
for all . From (2.9), the following inequality holds:

for all . Thus the function is quartic. Taking the limit in (2.33) with , satisfies (2.31) near the approximate function f of the functional equation (1.4). The remaining proof is similar to that of Theorem 2.9. This completes the proof. □
Theorem 2.12 Let be a ψ-approximatively radical quadratic function with . Assume that the function ψ is expansively superquadratic with a constant L satisfying . Then there exists a unique quartic function which satisfies (1.4) and the inequality
for all .
References
Ulam SM: A Collection of Mathematical Problems. Interscience, New York; 1960.
Ulam SM: Problems in Modern Mathematics. Wiley, New York; 1964.
Hyers DH: On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. J. Math. Soc. Jpn. 1950, 2: 64–66. 10.2969/jmsj/00210064
Bourgin DG: Classes of transformations and bordering transformations. Bull. Am. Math. Soc. 1951, 57: 223–237. 10.1090/S0002-9904-1951-09511-7
Rassias TM (Ed): Functional Equations, Inequalities and Applications. Kluwer Academic, Dordrecht; 2003.
Rassias TM: On the stability of functional equations and a problem of Ulam. Acta. Appl. Math. 2000, 62: 23–130. 10.1023/A:1006499223572
Rassias TM: On the stability of the linear function in Banach spaces. Proc. Am. Math. Soc. 1978, 72: 297–300. 10.1090/S0002-9939-1978-0507327-1
Rassias TM, Šemrl P: On the behavior of mappings which do not satisfy Hyers-Ulam stability. Proc. Am. Math. Soc. 1992, 114: 989–993. 10.1090/S0002-9939-1992-1059634-1
Rassias JM: Solution of a problem of Ulam. J. Approx. Theory 1989, 57: 268–273. 10.1016/0021-9045(89)90041-5
Rassias JM: On approximation of approximately linear functions by linear functions. J. Funct. Anal. 1982, 46: 126–130. 10.1016/0022-1236(82)90048-9
Forti GL: The stability of homomorphisms and amenability, with applications to functional equations. Abh. Math. Semin. Univ. Hamb. 1987, 57: 215–226. 10.1007/BF02941612
Gǎvruta P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive functions. J. Math. Anal. Appl. 1994, 184: 431–436. 10.1006/jmaa.1994.1211
Gajda Z, Ger R: Subadditive multifunctions and Hyers-Ulam stability. Intern. Schriftenreihe Numer. Math. 80. In General Inequalities 5. Birkhäuser, Basel; 1987:281–291.
Gruber PM: Stability of isometries. Trans. Am. Math. Soc. 1978, 245: 263–277.
Baktash E, Cho YJ, Jalili M, Saadati R, Vaezpour SM: On the stability of cubic mappings and quadratic mappings in random normed spaces. J. Inequal. Appl. 2008., 2008: Article ID 902187
Cho YJ, Gordji ME, Zolfaghari S: Solutions and stability of generalized mixed type QC functional equations in random normed spaces. J. Inequal. Appl. 2010., 2010: Article ID 403101
Cho YJ, Kang JI, Saadati R: Fixed points and stability of additive functional equations on the Banach algebras. J. Comput. Anal. Appl. 2012, 14: 1103–1111.
Cho YJ, Park C, Saadati R: Functional inequalities in non-Archimedean in Banach spaces. Appl. Math. Lett. 2010, 23: 1238–1242. 10.1016/j.aml.2010.06.005
Cho YJ, Saadati R: Lattice non-Archimedean random stability of ACQ functional equation. Adv. Differ. Equ. 2010. doi:10.1186/1687–1847–2011–31
Gordji ME, Kenary HA, Rezaei H, Lee YW, Kim GH: Solution and Hyers-Ulam-Rassias stability of generalized mixed type additive-quadratic functional equations in fuzzy Banach spaces. Abst. Appl. Anal. 2012., 2012: Article ID 953938
Gordji ME, Khodaei H, Ebadian A, Kim GH: Nearly radical quadratic functional equations in p -2-normed spaces. Abst. Appl. Anal. 2012., 2012: Article ID 896032
Gordji ME, Khodaei H: On the generalized Hyers-Ulam-Rassias stability of quadratic functional equations. Abst. Appl. Anal. 2009., 2009: Article ID 923476
Gordji ME, Parviz M:On the Hyers-Ulam stability of the functional equation . Nonlinear Funct. Anal. Appl. 2009, 14: 413–420.
Lee YH, Jung SM: A fixed point approach to the stability of an n -dimensional mixed-type additive and quadratic functional equation. Abst. Appl. Anal. 2012., 2012: Article ID 482936
Lee YH, Jung SM, Rassias TM: Stability of the n -dimensional mixed-type additive and quadratic functional equation in non-Archimedean normed spaces. Abst. Appl. Anal. 2012., 2012: Article ID 401762
Najati A, Cho YJ: Generalized Hyers-Ulam stability of the pexiderized Cauchy functional equation in non-Archimedean spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 309026
Najati A, Kang JI, Cho YJ: Local stability of the pexiderized Cauchy and Jensen’s equations in fuzzy spaces. J. Inequal. Appl. 2011, 2011: 78–85. doi:10.1186/1029–242x-2011–78 10.1186/1029-242X-2011-78
Park C, Cho YJ, Kenary HA: Orthogonal stability of a generalized quadratic functional equation in non-Archimedean spaces. J. Comput. Anal. Appl. 2012, 14: 526–535.
Saadati R, Cho YJ, Vahidi J: The stability of the quartic functional equation in various spaces. Comput. Math. Appl. 2010, 60: 1994–2002. 10.1016/j.camwa.2010.07.034
Savadkouhi MB, Gordji ME, Ghobadipur N:On the Cauchy-Rassias stability of the functional equation . Nonlinear Funct. Anal. Appl. 2009, 14: 665–675.
Lee SH, Im SM, Hawng IS: Quartic functional equations. J. Math. Anal. Appl. 2005, 307: 387–394. 10.1016/j.jmaa.2004.12.062
Tober J: Stability of Cauchy functional equation in quasi-Banach spaces. Ann. Pol. Math. 2004, 83: 243–255. 10.4064/ap83-3-6
Gordji ME, Khodaei H, Kim HM: Approximate quartic and quadratic mappings in quasi-Banach spaces. Int. J. Math. Math. Sci. 2011., 2011: Article ID 734567
Kang D: On the stability of generalized quartic mappings in quasi- β -normed spaces. J. Inequal. Appl. 2010., 2010: Article ID 198098
Rassias JM, Kim HM: Generalized Hyers-Ulam stability for general additive functional equation in quasi- β -normed spaces. J. Math. Anal. Appl. 2009, 356: 302–309. 10.1016/j.jmaa.2009.03.005
Ravi K, Rassias JM, Kodandan R: Generalized Ulam-Hyers stability of an AQ-functional equation in quasi-beta-normed spaces. Math. Aeterna 2011, 1: 217–236.
Khodaei H, Gordji ME, Kim SS, Cho YJ: Approximation of radical functional equations related to quadratic and quartic mappings. J. Math. Anal. Appl. 2012, 395: 284–297. 10.1016/j.jmaa.2012.04.086
Acknowledgements
This research was supported by Dongeui University (2011AA088) and the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (Grant Number: 2011-0021821).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment, and approved the finial manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, S.S., Cho, Y.J. & Eshaghi Gordji, M. On the generalized Hyers-Ulam-Rassias stability problem of radical functional equations. J Inequal Appl 2012, 186 (2012). https://doi.org/10.1186/1029-242X-2012-186
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-186
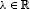 and ;
and ;