Comment on ‘Approximate ∗-derivations and approximate quadratic ∗-derivations on $C^{\ast }$-algebras’ [Jang, Park, J. Inequal. Appl. 2011 (2011), Article ID 55]

Abstract

In (J. Inequal. Appl. 2011:Article ID 55, Section 4, 2011), Jang and Park proved the Hyers-Ulam stability of quadratic ∗-derivations on Banach ∗-algebras. One can easily show that all the quadratic ∗-derivations δ in Section 4 must be trivial. So the results are trivial. In this paper, we correct the statements and prove the corrected results.

MSC:39B52, 47B47, 39B72.

1 Introduction and preliminaries

Suppose that $\mathcal{A}$ is a complex Banach ∗-algebra. A $\mathbb{C}$-linear mapping $\delta :D(\delta )\to \mathcal{A}$ is said to be a derivation on $\mathcal{A}$ if $\delta (ab)=\delta (a)b+a\delta (b)$ for all $a,b\in \mathcal{A}$, where $D(\delta )$ is a domain of δ and $D(\delta )$ is dense in $\mathcal{A}$. If δ satisfies the additional condition $\delta (a^{\ast })=\delta {(a)}^{\ast }$ for all $a\in \mathcal{A}$, then δ is called a ∗-derivation on $\mathcal{A}$. It is well known that if $\mathcal{A}$ is a $C^{\ast }$-algebra and $D(\delta )$ is $\mathcal{A}$, then the derivation δ is bounded.

A $C^{\ast }$-dynamical system is a triple $(\mathcal{A},G,\alpha )$ consisting of a $C^{\ast }$-algebra $\mathcal{A}$, a locally compact group G, and a pointwise norm continuous homomorphism α of G into the group $Aut(\mathcal{A})$ of ∗-automorphisms of $\mathcal{A}$. Every bounded ∗-derivation δ arises as an infinitesimal generator of a dynamical system for $\mathbb{R}$. In fact, if δ is a bounded ∗-derivation of $\mathcal{A}$ on a Hilbert space $\mathcal{H}$, then there exists an element h in the enveloping von Neumann algebra ${\mathcal{A}}^{\mathrm{\prime }\mathrm{\prime }}$ such that

$$\delta (x)=a{d}_{ih}(x)$$

for all $x\in \mathcal{A}$. The theory of bounded derivations of $C^{\ast }$-algebras is important in the quantum mechanics (see [2–4]).

A functional equation is called stable if any function satisfying the functional equation ‘approximately’ is near to a true solution of the functional equation.

In 1940, Ulam [5] proposed the following question concerning the stability of group homomorphisms: Under what condition does there exist an additive mapping near an approximately additive mapping? Hyers [6] answered the problem of Ulam for the case where $G_1$ and $G_2$ are Banach spaces. A generalized version of the theorem of Hyers for an approximately linear mapping was given by Rassias [7]. Since then, the stability problems of various functional equations have been extensively investigated by a number of authors (see [8–20]).

Jang and Park [[1], Section 4] proved the Hyers-Ulam stability of quadratic ∗-derivations on Banach ∗-algebras.

Theorem 1.1 ([[1], Theorem 4.2])

Suppose that $f:\mathcal{A}\to \mathcal{A}$ is a mapping with $f(0)=0$ for which there exists a function $\phi :{\mathcal{A}}^4\to [0,\mathrm{\infty })$ such that

$$\begin{array}{r}\tilde{\phi }(a,b,c,d):=\sum _{k=0}^{\mathrm{\infty }}\frac{1}{4^k}\phi (2^{k}a,2^{k}b,2^{k}c,2^{k}d)<\mathrm{\infty },\\ \parallel f(\lambda a+\lambda b+cd)+f(\lambda a-\lambda b+cd)-2{\lambda }^{2}f(a)-2{\lambda }^{2}f(b)-2f(c)d^2-2c^{2}f(d)\parallel \\ \le \phi (a,b,c,d),\\ \parallel f\left(a^{\ast }\right)-f{(a)}^{\ast }\parallel \le \phi (a,a,a,a)\end{array}$$

(1.1)

for all $a,b,c,d\in \mathcal{A}$ and all $\lambda \in \mathbb{T}:=\{\mu \in \mathbb{C}:|\mu |=1\}$. Also, if for each fixed $a\in \mathcal{A}$ the mapping $t\to f(ta)$ from to $\mathcal{A}$ is continuous, then there exists a unique quadratic ∗-derivation δ on $\mathcal{A}$ satisfying

$$\parallel f(a)-\delta (a)\parallel \le \frac{1}{4}\tilde{\phi }(a,a,0,0)$$

for all $a\in \mathcal{A}$.

Letting $\lambda =1$, $b=0$ and $d=I$ (identity) in (1.1) of Theorem 1.1, we get

$$\parallel f(a+c)+f(a+c)-2f(a)-2f(c)-2c^{2}f(I)\parallel \le \phi (a,0,c,I)$$

and

for all $a,c\in \mathcal{A}$. Thus $2\delta (a+c)=2\delta (a)+2\delta (c)+2c^2{d}^{\prime }$ for some $d^{\prime }\in \mathcal{A}$. Since δ is quadratic, $2\delta (a)+2\delta (-c)+2{(-c)}^2{d}^{\prime }=2\delta (a)+2\delta (c)+2c^2{d}^{\prime }$ and so $2\delta (a+c)=2\delta (a-c)$. Letting $c=a$ in the last equality, we get $2\delta (2a)=2\delta (0)=0$. So δ must be zero. Thus the results are trivial.

In this paper, we correct the wrong statements in [1] and prove the corrected results.

2 Hyers-Ulam stability of quadratic ∗-derivations on Banach ∗-algebras

In this section, we correct the statements of [[1], Section 4] and prove the Hyers-Ulam stability of the corrected results.

Definition 2.1 Let $\mathcal{A}$ be a ∗-normed algebra. A mapping $\delta :\mathcal{A}\to \mathcal{A}$ is a quadratic ∗-derivation on $\mathcal{A}$ if δ satisfies the following properties:

• (1) δ is a quadratic mapping,

• (2) δ is quadratic homogeneous, that is, $\delta (\lambda a)={\lambda }^2\delta (a)$ for all $a\in \mathcal{A}$ and all ,

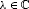• (3) $\delta (ab)=\delta (a)b^2+a^2\delta (b)$ for all $a,b\in \mathcal{A}$,

• (4) $\delta (a^{\ast })=\delta {(a)}^{\ast }$ for all $a\in \mathcal{A}$.

Example 2.2 Let $\mathcal{A}$ be a commutative ∗-normed algebra. For a given self-adjoint element $x\in \mathcal{A}$, let $\delta :\mathcal{A}\to \mathcal{A}$ be given by

$$\delta (a)=i(x{a}^2-a^{2}x)$$

for all $x\in \mathcal{A}$. Then it is easy to show that $\delta :\mathcal{A}\to \mathcal{A}$ is a quadratic ∗-derivation on $\mathcal{A}$.

Theorem 2.3 Suppose that $f:\mathcal{A}\to \mathcal{A}$ is a mapping with $f(0)=0$ for which there exists a function $\phi :{\mathcal{A}}^2\to [0,\mathrm{\infty })$ such that

(2.1)

(2.2)

(2.3)

for all $a,b,c,d\in \mathcal{A}$ and all $\lambda \in \mathbb{T}$. Also, if for each fixed $a\in \mathcal{A}$ the mapping $t\to f(ta)$ from to $\mathcal{A}$ is continuous, then there exists a unique quadratic ∗-derivation δ on $\mathcal{A}$ satisfying

$$\parallel f(a)-\delta (a)\parallel \le \frac{1}{4}\tilde{\phi }(a,a)$$

(2.4)

for all $a\in \mathcal{A}$.

Proof Putting $a=b$ and $\lambda =1$ in (2.1), we have

$$\parallel f(2a)-4f(a)\parallel \le \phi (a,a)$$

for all $a\in \mathcal{A}$. One can use induction to show that

$$\parallel \frac{f(2^{n}a)}{4^n}-\frac{f(2^{m}a)}{4^m}\parallel \le \frac{1}{4}\sum _{k=m}^{n-1}\frac{\phi (2^{k}a,2^{k}a)}{4^k}$$

(2.5)

for all $n>m\ge 0$ and all $a\in \mathcal{A}$. It follows from (2.5) that the sequence $\{\frac{f(2^{n}a)}{4^n}\}$ is Cauchy. Since $\mathcal{A}$ is complete, this sequence is convergent. Define

$$\delta (a):=\underset{n\to \mathrm{\infty }}{lim}\frac{f(2^{n}a)}{4^n}.$$

Since $f(0)=0$, we have $\delta (0)=0$. Replacing a and b by $2^{n}a$ and $2^{n}b$, respectively, in (2.1), we get

$$\parallel \frac{f(2^n(\lambda a+\lambda b))}{4^n}+\frac{f(2^n(\lambda a-\lambda b))}{4^n}-2{\lambda }^2\frac{f(2^{n}a)}{4^n}-2{\lambda }^2\frac{f(2^{n}b)}{4^n}\parallel \le \frac{\phi (2^{n}a,2^{n}b)}{4^n}.$$

Taking the limit as $n\to \mathrm{\infty }$, we obtain

$$\delta (\lambda a+\lambda b)+\delta (\lambda a-\lambda b)=2{\lambda }^2\delta (a)+2{\lambda }^2\delta (b)$$

(2.6)

for all $a,b\in \mathcal{A}$ and all . Putting $\lambda =1$ in (2.6), we obtain that δ is a quadratic mapping. It is well known that the quadratic mapping δ satisfying (2.4) is unique (see [4] or [20]).

Setting $b:=a$ in (2.6), we get

$$\delta (2\lambda a)=4{\lambda }^2\delta (a)$$

for all $a\in \mathcal{A}$ and all . Hence

$$\delta (\lambda a)={\lambda }^2\delta (a)$$

for all $a\in \mathcal{A}$ and all . Under the assumption that $f(ta)$ is continuous in for each fixed $a\in \mathcal{A}$, by the same reasoning as in the proof of [9], we obtain that $\delta (\lambda a)={\lambda }^2\delta (a)$ for all $a\in \mathcal{A}$ and all . Hence

$$\delta (\lambda a)=\delta (\frac{\lambda }{|\lambda |}|\lambda |a)=\frac{{\lambda }^2}{{|\lambda |}^2}\delta (|\lambda |a)=\frac{{\lambda }^2}{{|\lambda |}^2}{|\lambda |}^2\delta (a)={\lambda }^2\delta (a)$$

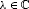for all $a\in \mathcal{A}$ and all ($\lambda \ne 0$). This means that δ is quadratic homogeneous.

Replacing c and d by $2^{n}c$ and $2^{n}d$, respectively, in (2.2), we get

for all $c,d\in \mathcal{A}$.

Thus we have

$$\parallel \delta (cd)-c^2\delta (d)-\delta (c)d^2\parallel \le \underset{n\to \mathrm{\infty }}{lim}\frac{\phi (2^{n}c,2^{n}d)}{4^n}=0.$$

Replacing a and $a^{\ast }$ by $2^{n}a$ and $2^n{a}^{\ast }$, respectively, in (2.3), we get

$$\parallel \frac{1}{4^n}f\left(2^n{a}^{\ast }\right)-\frac{1}{2^n}f{\left(4^{n}a\right)}^{\ast }\parallel \le \frac{1}{4^n}\phi (2^{n}a,2^{n}a).$$

Passing to the limit as $n\to \mathrm{\infty }$, we get the $\delta (a^{\ast })=\delta {(a)}^{\ast }$ for all $a\in \mathcal{A}$. So δ is a quadratic ∗-derivation on $\mathcal{A}$, as desired. □

Corollary 2.4 Let ε, p be positive real numbers with $p<2$. Suppose that $f:\mathcal{A}\to \mathcal{A}$ is a mapping such that

(2.7)

(2.8)

(2.9)

for all $a,b,c,d\in \mathcal{A}$ and all . Also, if for each fixed $a\in \mathcal{A}$ the mapping $t\to f(ta)$ is continuous, then there exists a unique quadratic ∗-derivation δ on $\mathcal{A}$ satisfying

$$\parallel f(a)-\delta (a)\parallel \le \frac{2\epsilon }{4-2^p}{\parallel a\parallel }^p$$

for all $a\in \mathcal{A}$.

Proof Putting $\phi (a,b)=\epsilon ({\parallel a\parallel }^p+{\parallel b\parallel }^p)$ in Theorem 2.3, we get the desired result. □

Similarly, we can obtain the following. We will omit the proof.

Theorem 2.5 Suppose that $f:\mathcal{A}\to \mathcal{A}$ is a mapping with $f(0)=0$ for which there exists a function $\phi :{\mathcal{A}}^2\to [0,\mathrm{\infty })$ satisfying (2.1), (2.2), (2.3) and

$$\sum _{k=1}^{\mathrm{\infty }}{4}^{2k}\phi (\frac{a}{2^k},\frac{b}{2^k})<\mathrm{\infty }$$

for all $a,b\in \mathcal{A}$. Also, if for each fixed $a\in \mathcal{A}$ the mapping $t\to f(ta)$ from to $\mathcal{A}$ is continuous, then there exists a unique quadratic ∗-derivation δ on $\mathcal{A}$ satisfying

$$\parallel f(a)-\delta (a)\parallel \le \frac{1}{4}\tilde{\phi }(a,a)$$

for all $a\in \mathcal{A}$, where

$$\tilde{\phi }(a,b):=\sum _{k=1}^{\mathrm{\infty }}{4}^k\phi (\frac{a}{2^k},\frac{b}{2^k}).$$

Corollary 2.6 Let ε, p be positive real numbers with $p>4$. Suppose that $f:\mathcal{A}\to \mathcal{A}$ is a mapping satisfying (2.7), (2.8) and (2.9). Also, if for each fixed $a\in \mathcal{A}$ the mapping $t\to f(ta)$ is continuous, then there exists a unique quadratic ∗-derivation δ on $\mathcal{A}$ satisfying

$$\parallel f(a)-\delta (a)\parallel \le \frac{2\epsilon }{2^p-4}{\parallel a\parallel }^p$$

for all $a\in \mathcal{A}$.

Proof Putting $\phi (a,b)=\epsilon ({\parallel a\parallel }^p+{\parallel b\parallel }^p)$ in Theorem 2.5, we get the desired result. □