- Research
- Open access
- Published:
The stability of functional equation min{f(x + y), f(x - y)} = |f(x) - f(y)|
Journal of Inequalities and Applications volume 2011, Article number: 22 (2011)
Abstract
In this paper, we prove the stability of the functional equation min {f(x + y), f(x - y)} = |f(x) - f(y)| in the class of real, continuous functions of real variable.
MSC2010: 39B82; 39B22
1. Introduction
In the paper [1], Simon and Volkmann examined functional equations connected with the absolute value of an additive function, that is,


and

where G is an abelian group and f : G → ℝ. The first two of them are satisfied by f(x) = |a(x)|, where a: G → ℝ is an additive function; moreover, the first one characterizes the absolute value of additive functions. The solutions of Equation (1.2) are appointed by Volkmann during the Conference on Inequalities and Applications in Noszwaj (Hungary, 2007), under the assumption that f : ℝ → ℝ is a continuous function. Namely, we have
Theorem 1.1 (Jarczyk and Volkmann [2]). Let f : ℝ → ℝ be a continuous function satisfying Equation (1.2). Then either there exists a constant c ≥ 0 such that f(x) = c|x|, x ∈ ℝ, or f is periodic with period 2p given by f(x) = c|x| with some constant c > 0, x ∈ [-p, p].
Actually, it is enough to assume continuity at a point, since this implies continuity on ℝ, see [2]. Moreover, some measurability assumptions force continuity. Baron in [3] showed that if G is a metrizable topological group and f : G → ℝ is Baire measurable and satisfies (1.2) then f is continuous. Kochanek and Lewicki (see [4]) proved that if G is metrizable locally compact group and f : G → ℝ is Haar measurable and satisfies (1.2), then f is continuous.
As already mentioned in [2], Kochanek noticed that every function f defined on an abelian group G which is of the form f = g ∘ a, where g : ℝ → ℝ is a solution of (1.2) described by Theorem 1.1 and a: G → ℝ is an additive function, is a solution of Equation (1.2).
Solutions of the Equation (1.3), according to [1], with the additional assumption that G is divisible by 6, are either f ≡ 0 or f = exp(|a|), where a: G → ℝ is an additive function. Without this additional assumption, however, we have the following remark (see [5]).
Remark 1.1. Let f : G → ℝ, where G is an abelian group. Then, f satisfies

if and only if
-
f ≡ 0
or
-
f = exp ∘|a|, for some additive function a
or
-
there is a subgroup G0 of G, such that

and

The result concerning stability of (1.1) was presented by Volkmann during the 45th ISFE in Bielsko-Biala (Poland, 2007) (for the proof see [2]) and superstability of (1.3) was proved in [6].
In this paper, we deal with the stability of Equation (1.2) in the class of continuous functions from ℝ to ℝ.
2. Main Result
We are going to prove
Theorem 2.1. If δ ≥ 0 and f : ℝ → ℝ is a continuous function satisfying

then either f is bounded (and in such a case is "close" to the solution F ≡ 0 of (1.2)) or there exists a constant c > 0 such that

that is, f is "close" to the solution F(x) = c|x| of (1.2).
We will write 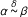 instead of |α - β | ≤ δ to shorten the notation.
instead of |α - β | ≤ δ to shorten the notation.
Notice that
-
if
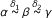 then
then 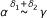 ,
, -
if
 then α ≤ γ +δ,
then α ≤ γ +δ, -
if
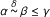 then α ≤ γ +δ,
then α ≤ γ +δ, -
if
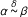 then for an arbitrary γ we have
then for an arbitrary γ we have  .
.
In the following lemma, we list some properties of functions satisfying (2.1) in more general settings.
Lemma 2.1. Let G be an abelian group, δ, ε ≥ 0 and let f : G → ℝ be an arbitrary function satisfying

Then
-
(i)
f(x) ≥ -δ, x ∈ G,
-
(ii)
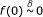
,
-
(iii)

, x ∈ G,
-
(iv)

, x ∈ G,
-
(v)
for every x, p ∈ G it holds

Proof. The first assertion follows from

The second one we get putting x = 0 in (2.4). Next, notice that, using (ii), we have

which proves (iii). Moreover,

so we obtain (iv). To prove (v), let us assume that  and choose an arbitrary x ∈ G. Since
and choose an arbitrary x ∈ G. Since

we have either

or

Let us consider the first possibility, the second can be dealt with in the analogous way. Notice that

which yields

The last inequality together with (2.5) finishes the proof of (v). □
Proof of Theorem 2.1. First, we notice that for every x,y, z ∈ ℝ such that x < y < z, we have

Indeed, assume that x, y, z ∈ ℝ, x < y < z and f(x) = f(z) > f(y) + 4δ. Let us choose the greatest x' ∈ [x, y] with f(x') = f(x) and the smallest z' ∈ [y, z] with f(z') = f(z). The continuity of f assures the existence of x'', z'' ∈ [x', z'], x'' < z'', such that f(x'') = f(z'') and z'' - x'' = y - x'. Of course,

Moreover, in view of (2.1), we have

So, if  , by Lemma 2.1(v), we would have
, by Lemma 2.1(v), we would have

which is impossible. Therefore, (2.7) implies  . Now, it is enough to put p = z'' + x''.
. Now, it is enough to put p = z'' + x''.
Assume that f is unbounded. We will show that

Suppose on the contrary that there exist x, y ∈ ℝ, 0 < x < y, with f(x) > f(y) + 6δ. From the unboundness of f and parts (i) and (iii) of Lemma 2.1, we infer that limx→∞f(x) = ∞. So we can find z1 > y with f(z1) = f(x). From (2.6) (with z = z1), we deduce that there exists p1 ≥ y + x such that  . Let us suppose that we have already defined p1, p2, ..., p
n
in such a way that
. Let us suppose that we have already defined p1, p2, ..., p
n
in such a way that  and p
k
≥ y + kx, k = 1, 2, ..., n. Notice that, in view of Lemma 2.1(i),
and p
k
≥ y + kx, k = 1, 2, ..., n. Notice that, in view of Lemma 2.1(i),

so we can find z
n
> p
n
with f(z
n
) = f(x). By (2.6) (with y = p
n
and z = z
n
), we obtain that there exists pn+1≥ p
n
+ x ≥ y + (n + 1)x such that  . Hence, we proved that there is a sequence (p
n
)n∈ℕincreasing to infinity such that
. Hence, we proved that there is a sequence (p
n
)n∈ℕincreasing to infinity such that  for n ∈ ℕ. Choose p > 0 satisfying
for n ∈ ℕ. Choose p > 0 satisfying  and such that
and such that

Let this maximum be taken at an x ∈ (0, p). Notice that f(2x) ≤ M + 4δ. This is obvious if 2x ≤ p, in the opposite case, if 2x > p, it follows from Lemma 2.1 part (v) and the fact that in such a case 2x -p ∈ [0, p), more precisely,

Let us now choose y > p with f(y) = 2M. We have

whence either  or
or  . Let us consider the first possibility, the second is analogous. From min{f (y - 2x), 2M) = min{f (y - 2x),
. Let us consider the first possibility, the second is analogous. From min{f (y - 2x), 2M) = min{f (y - 2x),  we deduce that f(y - 2x) ≤ 2δ. But 2δ ≥ f(y - 2x) ≥ min {f(y - 2x),
we deduce that f(y - 2x) ≤ 2δ. But 2δ ≥ f(y - 2x) ≥ min {f(y - 2x),  which contradicts (2.9) and, thereby, ends the proof of (2.8).
which contradicts (2.9) and, thereby, ends the proof of (2.8).
We infer that

whence

Notice that (2.8) implies

Thereby,

, for 0 < x < y, whence  for 0 < x < y. Consequently,
for 0 < x < y. Consequently,

Since f restricted to (0, ∞) is 19δ -approximately additive, there is an additive function a: (0, ∞) → ℝ such that  (see [7]). Moreover, since f is continuous, a(x) = cx for some positive c. Assertions (ii) and (iii) of Lemma 2.1 finish the proof of (2.2). □
(see [7]). Moreover, since f is continuous, a(x) = cx for some positive c. Assertions (ii) and (iii) of Lemma 2.1 finish the proof of (2.2). □
Remark. Kochanek noticed (oral communication) that we can decrease easily 21δ appearing in (2.2) to 19δ, by repeating the consideration from the proof, which we did for positive real halfline, for the negative real halfline. We would obtain  , for x > 0,
, for x > 0, 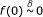 , and
, and  , for x < 0, where c, c' are some positive constants. But, since
, for x < 0, where c, c' are some positive constants. But, since  , x ∈ ℝ, we can deduce that c' = c.
, x ∈ ℝ, we can deduce that c' = c.
References
Simon (Chaljub-Simon) A, Volkmann P: Caractérisation du module d'une fonction à l'aide d'une équation fonctionnelle. Aequationes Math 1994, 47: 60–68. 10.1007/BF01838140
Jarczyk W, Volkmann P: On functional equations in connection with the absolute value of additive functions. Ser Math Catovic Debrecen 2010, 33: 1–11. [http://www.math.us.edu.pl/smdk]
Baron K: On Baire measurable solutions of some functional equations. Central Eur J Math 2009, 7: 804–808. 10.2478/s11533-009-0042-3
Kochanek T, Lewicki M: On measurable solutions of a general functional equation on topological groups. Publicationes Math Debrecen 2011, 78: 527–533.
Przebieracz B: On some Pexider-type functional equations connected with absolute value of additive functions Part I. Bull Austral Math Soc, in press.
Przebieracz B: Superstability of some functional equation. Ser Math Catovic Debrecen 2010, 31: 1–4. [http://www.math.us.edu.pl/smdk]
Kuczma M: An introduction to the theory of functional equations and inequalities, Cauchy's equation and Jensen's inequality. Prace Naukowe Uniwersytetu Śląskiego w Katowicach No. 489, PWN, Warszawa-Kraków-Katowice 1985.
Acknowledgements
This paper was supported by University of Silesia (Stability of some functional equations). The author wishes to thank prof. Peter Volkmann for valuable discussions. The author gratefully acknowledges the many helpful suggestions of an anonymous referee.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Przebieracz, B. The stability of functional equation min{f(x + y), f(x - y)} = |f(x) - f(y)|. J Inequal Appl 2011, 22 (2011). https://doi.org/10.1186/1029-242X-2011-22
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-22

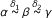 then
then 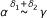 ,
, then α ≤ γ +δ,
then α ≤ γ +δ,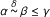 then α ≤ γ +δ,
then α ≤ γ +δ, .
.

