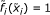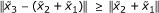- Research
- Open access
- Published:
A geometrical constant and normal normal structure in Banach Spaces
Journal of Inequalities and Applications volume 2011, Article number: 16 (2011)
Abstract
Recently, we introduced a new coefficient as a generalization of the modulus of smoothness and Pythagorean modulus such as J X , p (t). In this paper, We can compute the constant J X , p (1) under the absolute normalized norms on ℝ2 by means of their corresponding continuous convex functions on [0, 1]. Moreover, some sufficient conditions which imply uniform normal structure are presented.
2000 Mathematics Subject Classification: 46B20.
1. Introduction and preliminaries
We assume that X and X* stand for a Banach space and its dual space, respectively. By S X and B X we denote the unit sphere and the unit ball of a Banach space X, respectively. Let C be a non-empty bounded closed convex subset of a Banach space X. A mapping T : C → C is said to be non-expansive provided the inequality

holds for every x, y ∈ C. A Banach space X is said to have the fixed point property if every non-expansive mapping T : C → C has a fixed point, where C is a non-empty bounded closed convex subset of a Banach space X.
Recall that a Banach space X is called uniformly non-square if there exists δ > 0 such that ||x + y||/2 ≤ 1 - δ or ||x - y||/2 ≤ 1 - δ whenever x, y ∈ S X . A bounded convex subset K of a Banach space X is said to have normal structure if for every convex subset H of K that contains more than one point, there exists a point x0 ∈ H such that

A Banach space X is said to have uniform normal structure if there exists 0 < c < 1 such that for any closed bounded convex subset K of X that contains more than one point, there exists x0 ∈ K such that

It was proved by Kirk that every reflexive Banach space with normal structure has the fixed point property.
There are several constants defined on Banach spaces such as the James [1] and von Neumann-Jordan constants [2]. It has been shown that these constants are very useful in geometric theory of Banach spaces, which enable us to classify several important concept of Banach spaces such as uniformly non-squareness and uniform normal structure [3–8]. On the other hand, calculation of the constant for some concrete spaces is also of some interest [2, 5, 6, 9].
Recently, we introduced a new coefficient as a generalization of the modulus of smoothness and Pythagorean modulus such as J X , p (t).
Definition 1.1. Let x ∈ S X , y ∈ S X . For any t > 0, 1 ≤ p < ∞ we set

Some basic properties of this new coefficient are investigated in [6]. In particular, we compute the new coefficient in the Banach spaces l r , L r , l1, ∞ and give rough estimates of the constant in some concrete Banach spaces. In fact, the constant JX, p(1) is also important from the below Corollary in [6].
Corollary 1.2. If  . Then R(X) < 2, where R(X) and ω(X) stand for García-Falset constant and the coefficient of weak orthogonality, respectively (see [10, 11]). It is well known that a reflexive Banach space X with R(X) < 2 enjoys the fixed property (see [10]).
. Then R(X) < 2, where R(X) and ω(X) stand for García-Falset constant and the coefficient of weak orthogonality, respectively (see [10, 11]). It is well known that a reflexive Banach space X with R(X) < 2 enjoys the fixed property (see [10]).
In this paper, we compute the constant J X , p (1) under the absolute normalized norms on ℝ2, and give exact values of the constant J X , p (1) in some concrete Banach spaces. Moreover, some sufficient conditions which imply uniform normal structure are presented.
Recall that a norm on ℝ2 is called absolute if ||(z, w)|| = ||(|z|, |w|)|| for all z, w ∈ ℝ and normalized if ||(1,0)|| = ||(0,1)||. Let N α denote the family of all absolute normalized norms on ℝ2, and let Ψ denote the family of all continuous convex functions on [0, 1] such that ψ (1) = ψ (0) = 1 and max{1 - s, s} ≤ ψ(s) ≤ 1(0 ≤ s ≤ 1). It has been shown that N α and Ψ are a one-to-one correspondence in view of the following proposition in [12].
Proposition 1.3. If ||·||∈ N α , then ψ(s) = ||(1 - s, s)|| ∈ Ψ. On the other hand, if ψ(s) ∈Ψ, defined a norm ||·|| ψ as

then the norm ||·|| ψ ∈ N α .
A simple example of absolute normalized norm is usual l r (1 ≤ r ≤ ∞) norm. From Proposition 1.3, one can easily get the corresponding function of the l r norm:

Also, the above correspondence enable us to get many non-l r norms on ℝ2. One of the properties of these norms is stated in the following result.
Proposition 1.4. Let ψ, φ ∈ Ψ and φ ≤ ψ. Put  , then
, then

The Cesà ro sequence space was defined by Shue [13] in 1970. It is very useful in the theory of matrix operators and others. Let l be the space of real sequences.
For 1 < p < ∞, the Cesà ro sequence space ces p is defined by

The geometry of Cesà ro sequence spaces have been extensively studied in [14–16]. Let us restrict ourselves to the two-dimensional Cesà ro sequence space  which is just ℝ2 equipped with the norm defined by
which is just ℝ2 equipped with the norm defined by

2. Geometrical constant J X, p (1) and absolute normalized norm
In this section, we give a simple method to determine and estimate the constant J X, p (1) of absolute normalized norms on ℝ2. For a norm || · || on ℝ2, we write J X, p (1)(|| · ||) for J X, p (1)(ℝ2, || · ||). The following is a direct result of Proposition 2.4 in [6].
Proposition 2.1. Let X be a non-trivial Banach space. Then

Proposition 2.2. Let X be the space l r or L r [0, 1] with dimX ≥ 2 (see [6])
-
(1)
Let 1 < r ≤ 2 and 1/r + 1/r' = 1. Then for all t > 0
if 1 < p < r' then  .
.
if r' ≤ p < ∞ then  , for some K ≥ 1.
, for some K ≥ 1.
-
(2)
Let 2 ≤ r < ∞, 1 ≤ p < ∞ and h = max{r, p}. Then

Proposition 2.3. Let φ ∈ Ψ and ψ(s) = φ (1 - s). Then

Proof. For any x = (a, b) ∈ ℝ2 and a ≠ 0, b ≠ 0, put  . Then
. Then

Consequently, we have

We now consider the constant J X, p (1) of a class of absolute normalized norms on ℝ2. Now let us put

Theorem 2.4. Let ψ ∈ Ψ and ψ ≤ ψ
r
(2 ≤ r < ∞). If the function  attains its maximum at s = 1/ 2 and r ≥ p, then
attains its maximum at s = 1/ 2 and r ≥ p, then

Proof. By Proposition 1.4, we have || · || ψ ≤ || · || r ≤ M1|| · || ψ . Let x, y ∈ X, (x, y) ≠ (0, 0), where X = ℝ2. Then

from the definition of J X, p (t), implies that

Note that r ≥ p and the function  attains its maximum at s = 1/ 2, i.e.,
attains its maximum at s = 1/ 2, i.e., . From Proposition 2.2, implies that
. From Proposition 2.2, implies that

On the other hand, let us put x = (a, a), y = (a, -a), where  . Hence ||x||
ψ
= ||y||
ψ
= 1, and
. Hence ||x||
ψ
= ||y||
ψ
= 1, and

From (1) and (2), we have

Theorem 2.5. Let ψ ∈ Ψ and ψ ≥ ψ
r
(1 ≤ r ≤ 2). If the function  attains its maximum at s = 1/ 2 and 1 ≤ p < r', then
attains its maximum at s = 1/ 2 and 1 ≤ p < r', then

Proof. By Proposition 1.4, we have || · || r ≤ || · || ψ ≤ M2|| · || r . Let x, y ∈ X, (x, y) ≠ (0, 0), where X = ℝ2. Then

From the definition of J X, p (t), it implies that

note that 1 ≤ p < r' and the function  attains its maximum at s = 1/ 2, i.e.,
attains its maximum at s = 1/ 2, i.e., . From Proposition 2.2, it implies that
. From Proposition 2.2, it implies that

On the other hand, let us put x = (1, 0), y = (0, 1). Then ||x|| ψ = ||y|| ψ = 1, and

From (3) and (4), we have

Lemma 2.6 (see [6]). Let || · || and |.| be two equivalent norms on a Banach space. If a|.| ≤ || · || ≤ b|.| (b ≥ a > 0), then

Example 2.7. Let X = ℝ2 with the norm

Then

Proof. It is very easy to check that ||x|| = max{||x||2, λ||x||1} ∈ ℕ α and its corresponding function is

Therefore,

Since ψ2(s) attains minimum at s = 1/ 2 and hence  attains maximum at s = 1/ 2. Therefore, from Theorem 2.5, we have
attains maximum at s = 1/ 2. Therefore, from Theorem 2.5, we have

Example 2.8. Let X = ℝ2 with the norm

Then

Proof. It is obvious to check that the norm ||x|| = max{||x||2, λ||x||∞} is absolute, but not normalized, since ||(1, 0)|| = ||(0, 1)|| = λ. Let us put

Then |.| ∈ ℕ α and its corresponding function is

Then

Consider the increasing continuous function  . Because g(0) = 1 and
. Because g(0) = 1 and  , there exists a unique 0 ≤ a ≤ 1 such that g(a) = λ. In fact g(s) is symmetric with respect to s = 1/ 2. Then we have
, there exists a unique 0 ≤ a ≤ 1 such that g(a) = λ. In fact g(s) is symmetric with respect to s = 1/ 2. Then we have

Obviously, g(s) attains its maximum at s = 1/ 2. Hence, from Theorem 2.4 and Lemma 2.6, we have

Example 2.9. Let X = ℝ2 with the norm

Then

Proof. It is obvious to check that the norm  is absolute, but not normalized, since ||(1, 0)|| = ||(0, 1)|| = (1 + λ)1/ 2. Let us put
is absolute, but not normalized, since ||(1, 0)|| = ||(0, 1)|| = (1 + λ)1/ 2. Let us put

Therefore, |.| ∈ ℕ α and its corresponding function is

Obvious ψ(s) ≤ ψ2(s). Since  is symmetric with respect to s = 1/ 2, it suffices to consider
is symmetric with respect to s = 1/ 2, it suffices to consider  for s ∈ [0, 1/ 2]. Note that, for any s ∈ [0, 1/ 2], put
for s ∈ [0, 1/ 2]. Note that, for any s ∈ [0, 1/ 2], put  . Taking derivative of the function g(s), we have
. Taking derivative of the function g(s), we have

We always have g'(s) ≥ 0 for 0 ≤ s ≤ 1/ 2. This implies that the function g(s) is increased for 0 ≤ s ≤ 1/2. Therefore, the function  attains its maximum at s = 1/2. By Theorem 2.4 and Lemma 2.6, we have
attains its maximum at s = 1/2. By Theorem 2.4 and Lemma 2.6, we have

Example 2.10. (Lorentz sequence spaces). Let ω1 ≥ ω2> 0, 2 ≤ r < ∞. Two-dimensional Lorentz sequence space, i.e. ℝ2 with the norm

where  is the rearrangement of (|z|, |ω|) satisfying
is the rearrangement of (|z|, |ω|) satisfying  , then
, then

Proof. It is obvious that  , and the corresponding convex function is given by
, and the corresponding convex function is given by

Obviously ψ(s) ≤ ψ
r
(s) and  . It suffices to consider Φ(s) for s ∈ [0, 1/2] since Φ(s) is symmetric with respect to s = 1/2. Note that for s ∈ [0, 1/2]
. It suffices to consider Φ(s) for s ∈ [0, 1/2] since Φ(s) is symmetric with respect to s = 1/2. Note that for s ∈ [0, 1/2]

Some elementary computation shows that u(s) - v(s) = (1-(ω2/ω1))sr attains its maximum and v(s) attains its minimum at s = 1/2. Hence,

attains its maximum at s = 1/2 and so does Φ(s). Then by Theorem 2.4 and Lemma 2.6, we have

Example 2.11. Let X be two-dimensional Cesà ro space  , then
, then

Proof. We first define

for (x, y) ∈ ℝ2. It follows that  is isometrically isomorphic to (ℝ2, |.|) and |.| is an absolute and normalized norm, and the corresponding convex function is given by
is isometrically isomorphic to (ℝ2, |.|) and |.| is an absolute and normalized norm, and the corresponding convex function is given by

Indeed,  defined by
defined by  is an isometric isomorphism. We prove that ψ(s) ≥ ψ2(s). Note that
is an isometric isomorphism. We prove that ψ(s) ≥ ψ2(s). Note that

Consequently,

Some elementary computation shows that  attains its maximum at s = 1/2. Therefore, from Theorem 2.5, we have
attains its maximum at s = 1/2. Therefore, from Theorem 2.5, we have

3. Constant and uniform normal structure
First, we recall some basic facts about ultrapowers. Let l∞(X) denote the subspace of the product space IIn∈ℕX equipped with the norm ||(x
n
)|| := supn∈ℕ||x
n
|| < ∞. Let  be an ultrafilter on ℕ and let
be an ultrafilter on ℕ and let

The ultrapower of X, denoted by  , is the quotient space
, is the quotient space  equipped with the quotient norm. Write
equipped with the quotient norm. Write  to denote the elements of the ultrapower. Note that if
to denote the elements of the ultrapower. Note that if  is non-trivial, then X can be embedded into
is non-trivial, then X can be embedded into  isometrically. We also note that if X is super-reflexive, that is
isometrically. We also note that if X is super-reflexive, that is  , then X has uniform normal structure if and only if
, then X has uniform normal structure if and only if  has normal structure (see [17]).
has normal structure (see [17]).
Theorem 3.1. Let X be a Banach space with

for some t ∈ (0, 1]. Then X has uniform normal structure.
Proof. Observe that X is uniform non-square (see [6]) and then X is super-reflexive, it is enough to show that X has normal structure. Suppose that X lacks normal structure, then by Saejung [18, Lemma 2], there exist  and
and  satisfying:
satisfying:
-
(1)

and
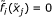 for all i ≠ j.
for all i ≠ j. -
(2)
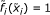
for i = 1, 2, 3.
-
(3)
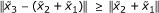
.
Let  and consider three possible cases.
and consider three possible cases.
First, if  . In this case, let us put
. In this case, let us put  and
and  . It follows that
. It follows that  , and
, and


Secondly, if  and
and  . In this case, let us put
. In this case, let us put  and
and  . It follows that
. It follows that  , and
, and


Thirdly,  and
and  . In this case, let us put
. In this case, let us put  and
and  . It follows that
. It follows that  , and
, and


Then, by definition of J
X, p
(t) and the fact  ,
,

This is a contradiction and thus the proof is complete.
References
Gao J, Lau KS: On two classes Banach spaces with uniform normal structure. Studia Math 1991, 99: 41–56.
Kato M, Maligranda L, Takahashi Y: On James and Jordan-von Neumann constants and normal structure coefficient of Banach spaces. Studia Math 2001, 144: 275–295. 10.4064/sm144-3-5
Zuo ZF, Cui Y: On some parameters and the fixed point property for multivalued nonexpansive mapping. J Math Sci Adv Appl 2008, 1: 183–199.
Zuo ZZ, Cui Y: A note on the modulus of U -convexity and modulus of W*-convexity. J Inequal Pure Appl Math 2008,9(4):1–7.
Zuo ZF, Cui Y: Some modulus and normal structure in Banach space. J Inequal Appl 2009, 2009: Article ID 676373.
Zuo ZF, Cui Y: A coefficient related to some geometrical properties of Banach space. J Inequal Appl 2009, 2009: Article ID 934321.
Zuo ZF, Cui Y: The application of generalization modulus of convexity in fixed point theory. J Nat Sci Heilongjiang Univ 2009, 2: 206–210.
Zuo ZF, Cui Y: Some sufficient conditions for fixed points of multivalued nonexpansive mappings. Fixed Point Theory Appl 2009, 2009: Article ID 319804.
Llorens-Fuster E: The Ptolemy and Zbǎganu constants of normed spaces. Nonlinear Anal 2010, 72: 3984–3993. 10.1016/j.na.2010.01.030
Garcia-Falset J: The fixed point property in Banach spaces with NUS-property. J Math Anal Appl 1997, 215: 532–542. 10.1006/jmaa.1997.5657
Sims B: A class of spaces with weak normal structure. Bull Aust Math Soc 1994, 50: 523–528.
Bonsall FF, Duncan J: Numerical Ranges II. London Mathematical Society Lecture Notes Series, vol. 10. Cambridge University Press, New York; 1973.
Shue JS: On the Ces à ro sequence spaces. Tamkang J Math 1970, 1: 143–150.
Cui Y, Jie L, Pluciennik R: Local uniform nonsquareness in Ces à ro sequence spaces. Comment Math 1997, 27: 47–58.
Cui Y, Hudik H: Some geometric properties related to fixed point theory in Ces à ro spaces. Collect Math 1999,50(3):277–288.
Maligranda L, Petrot N, Suantai S: On the James constant and B -convexity of Ces à ro and Ces à ro-Orlicz sequence spaces. J Math Anal Appl 2007,326(1):312–331. 10.1016/j.jmaa.2006.02.085
Khamsi MA: Uniform smoothness implies super-normal structure property. Nonlinear Anal 1992, 19: 1063–1069. 10.1016/0362-546X(92)90124-W
Saejung S: Sufficient conditions for uniform normal structure of Banach spaces and their duals. J Math Anal Appl 2007, 330: 597–604. 10.1016/j.jmaa.2006.07.087
Acknowledgements
The author wish to express their heartfelt thanks to the referees for their detailed and helpful suggestions for revising the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
ZZF designed and performed all the steps of proof in this research and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zuo, Z. A geometrical constant and normal normal structure in Banach Spaces. J Inequal Appl 2011, 16 (2011). https://doi.org/10.1186/1029-242X-2011-16
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-16


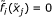 for all i ≠ j.
for all i ≠ j.