- Research
- Open access
- Published:
Weak solutions of functional differential inequalities with first-order partial derivatives
Journal of Inequalities and Applications volume 2011, Article number: 15 (2011)
Abstract
The article deals with functional differential inequalities generated by the Cauchy problem for nonlinear first-order partial functional differential equations. The unknown function is the functional variable in equation and inequalities, and the partial derivatives appear in a classical sense. Theorems on weak solutions to functional differential inequalities are presented. Moreover, a comparison theorem gives an estimate for functions of several variables by means of functions of one variable which are solutions of ordinary differential equations or inequalities. It is shown that there are solutions of initial problems defined on the Haar pyramid.
Mathematics Subject Classification: 35R10, 35R45.
1 Introduction
Two types of results on first-order partial differential or functional differential equations are taken into considerations in the literature. Theorems of the first type deal with initial problems which are local or global with respect to spatial variables, while the second one are concerned with initial boundary value problems. We are interested in results of the first type. More precisely, we consider initial problems which are local with respect to spatial variables. Then, the Haar pyramid is a natural domain on which solutions of differential or functional differential equations or inequalities are considered.
Hyperbolic differential inequalities corresponding to initial problems were first treated in the monographs [1]. (Chapter IX) and [2] (Chapters VII, IX). As is well known, they found applications in the theory of first-order partial differential equations, including questions such as estimates of solutions of initial problems, estimates of domains of solutions, estimates of the difference between solutions of two problems, criteria of uniqueness and continuous dependence of solution on given functions. The theory of monotone iterative methods developed in the monographs [3, 4] is based on differential inequalities.
Two different types of results on differential inequalities are taken into consideration in [1, 2]. The first type allows one to estimate a function of several variables by means of an another function of several variables, while the second type, the so-called comparison theorems give estimates for functions of several variables by means of functions of one variable, which are solutions of ordinary differential equations or inequalities.
There exist many generalizations of the above classical results. We list some of them below. Differential inequalities and the uniqueness of semi-classical solutions to the Cauchy problem for the weakly coupled systems were developed in [5] (Chapter VIII). Hyperbolic functional differential inequalities and suitable comparison results for initial problems are given in [6, 7] (Chapter I). Infinite systems of functional differential equations and comparison results are discussed in [8, 9]. Impulsive partial differential inequalities were investigated in [10]. A result on implicit functional differential inequalities can be found in [11]. Differential inequalities with unbounded delay are investigated in [12]. Functional differential inequalities with Kamke-type comparison problems can be found in [13]. Viscosity solutions of functional differential inequalities were studied in [14, 15].
The aim of this article is to add a new element to the above sequence of generalizations of classical theorems on differential inequalities.
We now formulate our functional differential problem. For any metric spaces, U and V, we denote by C(U, V) the class of all continuous functions from U into V. We use vectorial inequalities with the understanding that the same inequalities hold between their corresponding components. Suppose that  , a > 0, ℝ+ = [0, + ∞), is nondecreasing and M(0) = 0[n]where 0[n]= (0, ..., 0) ∈ ℝn. Let E be the Haar pyramid:
, a > 0, ℝ+ = [0, + ∞), is nondecreasing and M(0) = 0[n]where 0[n]= (0, ..., 0) ∈ ℝn. Let E be the Haar pyramid:

where b ∈ ℝn and b > M(a). Write E0 = [-b0, 0] × [-b, b] where b0 ∈ ℝ+. For (t, x) ∈ E define

Then, D[t, x] = D0[t, x]∪[D⋆[t, x] where

Write r0 = -b0 - a, r = 2b and B = [-r0, 0] × [-r, r]. Then, D[t, x] ⊂ B for (t, x) ∈ E. Given z: E0 ∪ E → ℝ and (t, x) ∈ E, define z(t, x): D[t, x] → ℝ by z(t, x)(τ, s) = z(t + τ, x + s), (τ, s) ∈ D[t, x]. Then z(t, x)is the restriction of z to the set (E0 ∪ E) ∩ ([-b0, t] × ℝn) and this restriction is shifted to D[t, x].
Put Ω = E × ℝ × C(B, ℝ) × ℝn and suppose that f : Ω → ℝ is a given function of the variables (t, x, p,w, q), x = (x1, ..., x n ), q = (q1, ..., q n ). Let us denote by z an unknown function of the variables (t, x). Given ψ: E0 → ℝ, we consider the functional differential equation:

with the initial condition

where  . We will say that f satisfies condition (V ), if for each (t, x, p, q) ∈ E × ℝ × ℝn and for w,
. We will say that f satisfies condition (V ), if for each (t, x, p, q) ∈ E × ℝ × ℝn and for w,  such that
such that  for (τ, s) ∈ D[t, x] then we have
for (τ, s) ∈ D[t, x] then we have  . It is clear that condition (V) means that the value of f at the point (t, x, p,w, q) ∈ Ω depends on (t, x, p, q) and on the restriction of w to the set D[t, x] only.
. It is clear that condition (V) means that the value of f at the point (t, x, p,w, q) ∈ Ω depends on (t, x, p, q) and on the restriction of w to the set D[t, x] only.
We assume that F satisfies condition (V). Let us write

We consider weak solutions of initial problems. A function  where 0 < c ≤ a, is a weak solution of (1), (2) provided
where 0 < c ≤ a, is a weak solution of (1), (2) provided
-
(i)

is continuous, and
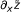 exists on E ∩ ([0, c] × ℝn) and
exists on E ∩ ([0, c] × ℝn) and  for t ∈ [0, c],
for t ∈ [0, c], -
(ii)
for x ∈ [-b, b], the function
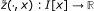 is absolutely continuous,
is absolutely continuous, -
(iii)
for each x ∈ [-b, b], the function
 satisfies equation 1 for almost all t ∈ I[x] ∩ [0, c] and condition (2) holds.
satisfies equation 1 for almost all t ∈ I[x] ∩ [0, c] and condition (2) holds.
This class of solutions for nonlinear equations was introduced and widely studied in nonfunctional setting by Cinquini and Cinquini Cibrario [16, 17].
The paper is organized as follows. In Sections 2 and 3 we present theorems on functional differential inequalities corresponding to (1), (2). They can be used for investigations of solutions to (1), (2). We show that the set of solutions is not empty. In Section 4 we prove that there is a weak solution to (1), (2) defined on E c where c ∈ (0, a] is a sufficiently small constant.
2 Functional differential inequalities
Let  , [τ, t] ⊂ ℝ, be the class of all integrable functions Ψ: [τ, t] → ℝn. The maximum norm in the space C(B, ℝ) will be denoted by ||·||
B
. We will need the following assumptions on given functions.
, [τ, t] ⊂ ℝ, be the class of all integrable functions Ψ: [τ, t] → ℝn. The maximum norm in the space C(B, ℝ) will be denoted by ||·||
B
. We will need the following assumptions on given functions.
Assumption H0. The function f : Ω → ℝ satisfies the condition (V) and
-
(1)
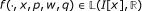
where (x, p,w, q) ∈ [-b, b] × ℝ × C(B, ℝ) × ℝn and f(t, ·): S t × ℝ × C(B, ℝ) × ℝn → ℝ is continuous for almost all t ∈ [0, a],
-
(2)
there exist the derivatives
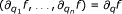 and
and  where (x, p,w,q) ∈ [-b, b] × ℝ × C(B, ℝ) × ℝn, and the function ∂
q
f(t, ·): S
t
× ℝ × C(B, ℝ) × ℝn → ℝn is continuous for almost all t ∈ [0, a],
where (x, p,w,q) ∈ [-b, b] × ℝ × C(B, ℝ) × ℝn, and the function ∂
q
f(t, ·): S
t
× ℝ × C(B, ℝ) × ℝn → ℝn is continuous for almost all t ∈ [0, a], -
(3)
there is
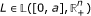 , L = (L1, ..., L
n
), such that
, L = (L1, ..., L
n
), such that 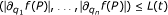 where P = (t, x, p,w, q) ∈ Ω, and
where P = (t, x, p,w, q) ∈ Ω, and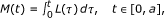 (3)
(3) -
(4)
there is
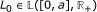 such that
such that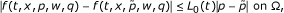 (4)
(4) -
(5)
f is nondecreasing with respect to the functional variable and
 ,
,  and
and -
(i)
the derivatives
 ,
, 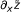 exist on E and
exist on E and 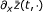 ,
,  for t ∈ [0, a],
for t ∈ [0, a], -
(ii)
for each x ∈ [-b, b] the functions
 ,
, 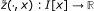 are absolutely continuous.
are absolutely continuous.
We start with a theorem on strong inequalities. Write

Theorem 2.1. Suppose that Assumption H0 is satisfied and
(1) for each x ∈ [-b, b], the functional differential inequality

is satisfied for almost all t ∈ I[x],
(2)  for (t,x) ∈ E0 and
for (t,x) ∈ E0 and

Under these assumptions, we have

Proof Suppose by contradiction, that assertion (7) fails to be true. Then, the set

is not empty. Put  A+. From (6), we conclude that
A+. From (6), we conclude that  and there is
and there is  such that
such that

and

Write

where  . It follows from (5) and (8) that for x ∈ [-b, b] and for almost all
. It follows from (5) and (8) that for x ∈ [-b, b] and for almost all  , we have
, we have

Set

We conclude from the Hadamard mean value theorem that

Let us denote by g(·, t, x) the solution of the Cauchy problem:

where (t, x) ∈ E and  . Suppose that [t0, t] is the interval on which the solution g(·, t, x) is defined. Then,
. Suppose that [t0, t] is the interval on which the solution g(·, t, x) is defined. Then,

and consequently,

We conclude that (τ, g(τ, t, x)) ∈ E for τ ∈ [t0, t] and, consequently, the function g(·, t, x) is defined on [0, t]. It follows from (10) that

Where  . We conclude from (8), (13) that
. We conclude from (8), (13) that

This gives

and consequently  which contradicts (9). Hence, A+ is empty and the statement (7) follows.
which contradicts (9). Hence, A+ is empty and the statement (7) follows.
Now we prove that a weak initial inequality for  and
and  on E0 and weak functional differential inequalities on E imply weak inequality for
on E0 and weak functional differential inequalities on E imply weak inequality for  and
and  on E.
on E.
Assumption H[σ]. The function σ : [0, a] × ℝ+ → ℝ+ satisfies the conditions:
-
(1)
σ (t, ·): ℝ+ → ℝ+ is continuous for almost all t ∈ [0, a],
-
(2)
σ (·, p): [0, a] → ℝ+ is measurable for every p ∈ → ℝ+ and there is
 such
such
that σ (t, p) ≤ m σ (t) for p ∈ ℝ+ and for almost all t ∈ [0, a],
-
(3)
the function
 for t ∈ [0, a] is the maximal solution of the Cauchy problem:
for t ∈ [0, a] is the maximal solution of the Cauchy problem: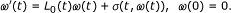
Theorem 2.2. Suppose that Assumptions H0 and H[σ] are satisfied and
(1) the estimate

holds on Ω for ,
,
(2)  for (t, x) ∈ E0, and for each x ∈ [-b, b] the functional differential inequality
for (t, x) ∈ E0, and for each x ∈ [-b, b] the functional differential inequality

is satisfied for almost all t ∈ I[x].
Under these assumptions, we have

Proof Let us denote by ω(·, ε), ε > 0, the right-hand maximal solution of the Cauchy problem

There is ε0 > 0 such that, for every 0 < ε < ε0, the solution ω(·, ε) is defined on [0, a] and

Let  be defined by
be defined by

Then, we have  on E0. We prove that for each x ∈ [-b, b] the functional differential inequality
on E0. We prove that for each x ∈ [-b, b] the functional differential inequality

is satisfied for almost all t ∈ I[x]. It follows from (4), (14), that

which completes the proof of (17). It follows from Theorem 2.1 that  on E. From this inequality, we obtain in the limit, letting ε tend to zero, inequality (16). This completes the proof.
on E. From this inequality, we obtain in the limit, letting ε tend to zero, inequality (16). This completes the proof.
The results presented in Theorems 2.1 and 2.2 have the following properties. In both the theorems, we have assumed that  on E0. It follows from Theorem 2.1 that the strong inequality (6) and the strong functional differential inequality (5) for almost all t ∈ I[x] imply the strong inequality (7). Theorem 2.2 shows that the weak initial inequality
on E0. It follows from Theorem 2.1 that the strong inequality (6) and the strong functional differential inequality (5) for almost all t ∈ I[x] imply the strong inequality (7). Theorem 2.2 shows that the weak initial inequality  on E and the weak functional differential inequality (15) for almost all t ∈ I[x] imply the weak inequality (16).
on E and the weak functional differential inequality (15) for almost all t ∈ I[x] imply the weak inequality (16).
In the next two lemmas, we assume that  on E0 and we prove that the strong initial inequality (6) and the weak functional inequality (15) imply the strong inequality (7).
on E0 and we prove that the strong initial inequality (6) and the weak functional inequality (15) imply the strong inequality (7).
We prove also that the weak initial inequality  on E0 and the strong functional differential inequality (5) imply the inequality
on E0 and the strong functional differential inequality (5) imply the inequality  for (t, x) ∈ E, 0 < t ≤ a.
for (t, x) ∈ E, 0 < t ≤ a.
Lemma 2.3. Suppose that Assumptions H0 and H[σ] are satisfied and
(1) the estimate (14) holds on Ω for  ,
,
(2)  for (t, x) ∈ E0 and for each x ∈ [-b, b] the functional differential inequality (5) is satisfied for almost all t ∈ I[x].
for (t, x) ∈ E0 and for each x ∈ [-b, b] the functional differential inequality (5) is satisfied for almost all t ∈ I[x].
Under these assumption, we have  for (t, x) ∈ E, 0 < t ≤ a.
for (t, x) ∈ E, 0 < t ≤ a.
Proof It follows from Theorem 2.2 that  for (t, x) ∈ E. Suppose that there is
for (t, x) ∈ E. Suppose that there is  , such that
, such that  . By repeating the argument used in the proof of Theorem 2.1, we obtain
. By repeating the argument used in the proof of Theorem 2.1, we obtain

where g(·, t, x) is the solution to (12). Then,  , which completes the proof of the lemma.
, which completes the proof of the lemma.
Lemma 2.4. Suppose that Assumption H0 and H[σ] are satisfied and
(1) the estimate (14) holds on Ω for  ,
,
(2)  for (t, x) ∈ E0 and
for (t, x) ∈ E0 and  for x∈ [-b, b],
for x∈ [-b, b],
(3) for each x ∈ [-b, b] the functional differential inequality (15) is satisfied for almost all t ∈ I[x].
Under these assumption, we have

Proof Let

For δ > 0, we denote by ω(·, δ) the solution of the Cauchy problem

There is δ0 > 0 such that for 0 < δ ≤ δ0, we have

Let us denote by  a continuous function such that
a continuous function such that  on E0 and
on E0 and  for x ∈ [-b, b]. Suppose that z⋆: E0 ∪ E → ℝ is defined by
for x ∈ [-b, b]. Suppose that z⋆: E0 ∪ E → ℝ is defined by

where 0 < δ ≤ δ0. We prove that

Note that  on E0 and
on E0 and  for x ∈ [-b, b]. We prove that for each x ∈ [-b, b], the functional differential inequality
for x ∈ [-b, b]. We prove that for each x ∈ [-b, b], the functional differential inequality

is satisfied for almost all t ∈ I[x]. By Assumption H0 and (19), we have

which completes the proof of (22). We get from Theorem 2.1 that (21 holds. Inequalities (20), (21), imply (18), which completes the proof of the lemma.
Remark 2.5. The results presented in Section 2 can be extended on functional differential inequalities corresponding to the system:

where z = (z1, ..., z k ) and f = (f1, ..., f k ): E × ℝk × C(B, ℝk) × ℝn → ℝn is a given function of the variables (t, x, p,w, q), p = (p1, ..., p k ), w = (w1, ..., w k ), Some quasi-monotone assumptions on the function f with respect to p are needed in this case.
3 Comparison theorem
For z ∈ C(E0 ∪ E, ℝ), we put

Assumption H⋆. The functions Δ: E × C(B, ℝ) → ℝn, Δ = (Δ1, ..., Δ n ), and ϱ: [0, a] × ℝ+ → ℝ+ satisfy the conditions:
-
(1)
Δ satisfies condition (V) and
 where (x, w) ∈ [-b, b] × C(B, ℝ) and Δ(t, ·): S
t
× C(B, ℝ) → ℝn is continuous for almost all t ∈ [0, a],
where (x, w) ∈ [-b, b] × C(B, ℝ) and Δ(t, ·): S
t
× C(B, ℝ) → ℝn is continuous for almost all t ∈ [0, a], -
(2)
there is
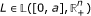 , L = (L1, ..., L
n
), such that
, L = (L1, ..., L
n
), such that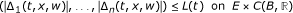
and  is given by (3),
is given by (3),
-
(3)
ϱ(·, p): [0, a] → ℝ+ is measurable for p ∈ ℝ+ and ϱ(t, ·): ℝ+ → ℝ+ is continuous and nondecreasing for almost all t ∈ [0, a], and there is
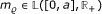 such that ϱ(t, p) ≤ m ϱ(t) for p ∈ ℝ+ and for almost all t ∈ [0, a],
such that ϱ(t, p) ≤ m ϱ(t) for p ∈ ℝ+ and for almost all t ∈ [0, a], -
(4)
z⋆: E0 ∪ E → ℝ is continuous and
-
(i)
the derivatives
 exist on E and ∂
x
z⋆(t, ·) ∈ C(S
t
, ℝn) for t ∈ [0, a],
exist on E and ∂
x
z⋆(t, ·) ∈ C(S
t
, ℝn) for t ∈ [0, a], -
(ii)
for each x ∈ [-b, b] the function z⋆(·, x): I[x] → ℝ is absolutely continuous.
Theorem 3.1. Suppose that Assumption H ⋆ is satisfied and
(1) for each x ∈ [-b, b] the functional differential inequality

is satisfied for almost all t ∈ I[x],
(2) the number η ∈ ℝ+ is defined by the relation: |z⋆(t, x)| ≤ η for (t, x) ∈ E0.
Under these assumptions we have

where ω(·, η) is the maximal solution of the Cauchy problem

Proof Let us denote by g[z⋆](·, t, x) the solution of the Cauchy problem

where (t, x) ∈ E. It follows from condition 1) of Assumption H⋆ that g[z⋆](·, t, x) is defined on [0, t]. We conclude from (23) that for each x ∈ [-b, b], the differential inequality

is satisfied for almost all τ ∈ [0, t]. This gives the integral inequality

The function ω(·, η) satisfies the integral equation corresponding to the above inequality. From condition 3) of Assumption H⋆ we obtain (24), which completes the proof.
We give an estimate of the difference between two solutions of equation 1.
Theorem 3.2. Suppose that the function f : Ω → ℝ satisfies condition (V) and
(1) conditions (1)-(3) of Assumption H0 hold,
(2) there is ϱ : [0, a] × ℝ+ → ℝ+ such that condition (3) of Assumption H ⋆ is satisfied and

(3) the functions  ,
,  are weak solutions to (1) and η ∈ ℝ+ is defined by the relation:
are weak solutions to (1) and η ∈ ℝ+ is defined by the relation:  for (t, x) ∈ E0.
for (t, x) ∈ E0.
Under these assumptions, we have

where ω(·, η) is the maximal solution to (25).
Proof Let us write

Then, for each x ∈ [-b, b] and for almost all t ∈ I[x], we have

Set  . It follows from the Hadamard mean value theorem that
. It follows from the Hadamard mean value theorem that

where D(t, xξ) is given by (11). We conclude from (26 that

Thus, we see that for each x ∈ [-b, b] the functional differential inequality

is satisfied for almost all ∈ I[x]. From Theorem 3.1 we obtain (27), which completes the proof.
The next lemma on the uniqueness of weak solutions is a consequence of Theorem 3.2.
Lemma 3.3. Suppose that the function f : Ω → ℝ satisfies condition (V ) and
(1) assumptions (1), (2) of Theorem 3.2 hold,
(2) the function  for t ∈ [0, a] is the maximal solution to (25) with η = 0.
for t ∈ [0, a] is the maximal solution to (25) with η = 0.
Then, problem (1), (2) admits one weak solution at the most.
Proof From (27) we deduce that for η = 0 we have  on E and the lemma follows.
on E and the lemma follows.
4 Existence of solutions of initial problems
Put Ξ = E × C(B, ℝ) × ℝn and suppose that F : Ξ → ℝ is a given function of the variables (t, x, w, q). Given ψ : E0 → ℝ, we consider the functional differential equation:

with the initial condition

We assume that F satisfies condition (V) and we consider weak solutions to (28), (29).
Let us denote by Mn × nthe class of all n × n matrices with real elements. For x ∈ ℝn, W ∈ Mn × n, where x = (x1, ..., x n ), W = [w ij ]i,j = 1,...,n, we put

If W ∈ Mn × n, then W T denotes the transpose matrix. Suppose that v ∈ C(E0 ∪ R, ℝn), U ∈ C(E0 ∪ R, Mn × n). The following seminorms will be needed in our considerations:

where t ∈ [0, a]. The scalar product in ℝn will be denoted by "∘". We will use the symbol CL(B, ℝ) to denote the class of all linear and continuous operators defined on C(B, ℝ) and taking values in ℝ. The norm in the space CL(B, ℝ) generated by the maximum norm in C(B, ℝ) will be denoted by ||·||⋆. The maximum norms in C(E0, ℝ) and C(E0, ℝn) will be denoted by  and
and  , respectively.
, respectively.
Assumption H0[F ]. The function F : Ξ → ℝ satisfies the condition (V ) and
-
(1)
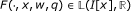
where (x, w, q) ∈ [-b, b] × C(B, ℝ) × ℝn and F(t, ·): S t × C(B, ℝ) × ℝn → ℝ is continuous for almost all t ∈ [0, a],
-
(2)
there is
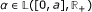 such that
such that
where θ ∈ C(B, ℝ) is given by θ (τ, s) = 0 on B,
-
(3)
for P = (t, x, w, q) ∈ Ξ there exist the derivatives
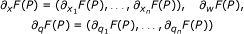
and  and
and  where (x, w, q) ∈ [-b, b] × C(B, ℝ) × ℝn,
where (x, w, q) ∈ [-b, b] × C(B, ℝ) × ℝn,  ,
,
-
(4)
the functions
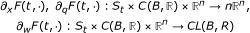
are continuous for almost all t ∈ [0, a] and there are 
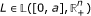 , L = (L1, ..., L
n
), such that
, L = (L1, ..., L
n
), such that

and

where (t, x, w, q) ∈ Ξ, and  is given by (3).
is given by (3).
Now we define some function spaces. Given  , we denote by
, we denote by  the set of all ψ ∈ C(E0, ℝ) such that
the set of all ψ ∈ C(E0, ℝ) such that
-
(i)
the derivatives
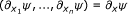 exist on E0 and ∂
x
ψ ∈ C(E0 , ℝn),
exist on E0 and ∂
x
ψ ∈ C(E0 , ℝn), -
(ii)
the estimates
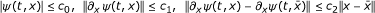
are satisfied on E0.
Let  be given and 0 < c ≤ a. We denote by Cψ.cthe class of all z ∈ C(E
c
, R) such that z(t, x) = ψ (t, x) on E0. For the above ψ and c we denote by C∂ψ.cthe class of all v ∈ C(Ec, ℝn) such that v(t, x) = ∂
x
ψ(t, x) on E0.
be given and 0 < c ≤ a. We denote by Cψ.cthe class of all z ∈ C(E
c
, R) such that z(t, x) = ψ (t, x) on E0. For the above ψ and c we denote by C∂ψ.cthe class of all v ∈ C(Ec, ℝn) such that v(t, x) = ∂
x
ψ(t, x) on E0.
Suppose that Assumption H0[F] is satisfied and  , z ∈ Cψ.c, u ∈ C∂ψ.cwhere 0 < c ≤ a. We consider the Cauchy problem
, z ∈ Cψ.c, u ∈ C∂ψ.cwhere 0 < c ≤ a. We consider the Cauchy problem

where (t, x) ∈ E and 0 ≤ t ≤ c. Let us denote by g[z, u](·, t, x) the solution of (30). The function g[z, u](·, t, x) is the bicharacteristic of (28) corresponding to (z, u).
For u ∈ C∂ψ.c, u = (u1, ..., u n ), and P ∈ Ξ, (t, x) ∈ E ∩ ([0, c] × ℝn), we write

Set

Let  be defined by
be defined by

and

Set  where
where

and

We consider the system of integral functional equations

System (35) is obtained in the following way. We first introduce an additional unknown function u = ∂ x z in (28). Then, we consider the linearization of (28) with respect to the last variable, and we obtain the equation

By virtue of (28) we get the following differential equation for the unknown function u ::

Finally, we put u = ∂ x z in (37). If we consider (36) and (37) along the bicharacteristic g[z, u](·, t, x), then we obtain

and

By integrating of (38) and (39) on [0, t] with respect to τ, we get (35).
We prove that there is a solution  to (35) defined on E
c
where c ∈ (0, a] is sufficiently a small constant, and
to (35) defined on E
c
where c ∈ (0, a] is sufficiently a small constant, and  and
and  are weak solutions to (28), (29). We first give estimates of solutions to (35).
are weak solutions to (28), (29). We first give estimates of solutions to (35).
Lemma 4.1. Suppose that Assumption H0[F] is satisfied and
(1)  and 0 < c ≤ a.
and 0 < c ≤ a.
(2) the functions  ,
,  are continuous and they satisfy (35).
are continuous and they satisfy (35).
Then

where

Proof. Write

It follows from Assumption H0[F] and from (31) - (34) that  satisfy the integral inequalities
satisfy the integral inequalities

where t ∈ [0, c]. The functions  satisfy integral equations corresponding to the above inequalities. This proves the lemma.
satisfy integral equations corresponding to the above inequalities. This proves the lemma.
Suppose that ζ, χ : [0, c] → ℝ+ are continuous and they satisfy the integral inequalities

where t ∈ [0, c]. It is clear that  satisfy the above conditions.
satisfy the above conditions.
Given d, h ∈ ℝ+, d ≥ c1, h ≥ c2 and 0 < c ≤ a. Suppose that  . We denote by Cψ.c[ζ, d] the class of all z ∈ Cψ.csuch that
. We denote by Cψ.c[ζ, d] the class of all z ∈ Cψ.csuch that

For the above ψ , we denote by C∂ψc[χ, h] the class of all  satisfying the conditions
satisfying the conditions

Write A = ζ(a), C = χ(a) and  where
where

Assumption H[F]. The function F : Ξ → ℝ satisfies Assumption H0[F], and there is  such that the terms
such that the terms

are bounded from above on Ξ[A,C] by 
Remark 4.2. It is important that we have assumed the Lipschitz condition for ∂
x
F, ∂
w
F, ∂
q
F for satisfying the condition: ||w||
B
,
satisfying the condition: ||w||
B
,  .
.
There are differential integral equations and differential equations with deviated variables such that Assumption H[F] is satisfied and the functions ∂ x F, ∂ w F, and ∂ q F do not satisfy the Lipschitz condition with respect to the functional variable on Ξ.
It is clear that there are functional differential equations which satisfy Assumptions H[F] and they do not satisfy the assumptions of the existence theorem presented in [18].
Lemma 4.3. Suppose that Assumption H[F], H[φ] are satisfied and

where 0 < c ≤ a.
Then the bicharacteristics g[z, u](·, t, x) and  exist on intervals [0, δ[z, u](t, x)] and
exist on intervals [0, δ[z, u](t, x)] and such that for τ = δ[z, u](t, x),
such that for τ = δ[z, u](t, x),  , we have (τ, g[z, u](τ, t, x)) ∈ ∂E
c
,
, we have (τ, g[z, u](τ, t, x)) ∈ ∂E
c
,  , where ∂E
c
is the boundary of E
c
.
, where ∂E
c
is the boundary of E
c
.
The solution of (30) is unique, and we have the estimates

and

where  ,
,  , τ ∈ [0, c].
, τ ∈ [0, c].
Proof The existence and uniqueness of the solution to (30) follows from classical theorems on Carathéodory solutions of ordinary differential equations. We conclude from Assumption H[F] that the integral inequalities

and

are satisfied. Then, we obtain (40) and (41) from the Gronwall inequality.
Write

Assumption H[c]. The constants c ∈ (0, a], d, h > 0 satisfy the relations: Λ(c) ≤ d, Γ(c) ≤ h.
Remark 4.4. If we assume that

then there is c ∈ (0, a] such that Λ(c) ≤ d and Γ(c) ≤ h.
Theorem 4.5. Suppose that Assumptions H[F], H[c] are satisfied and  . Then there is a solution
. Then there is a solution of (28), (29).
of (28), (29).
If
 and
and
 is a solution to (28) with the initial condition
is a solution to (28) with the initial condition

then there is C⋆ ∈ ℝ+ such that for t ∈ [0, c], we have.

Proof The proof will be divided into four steps
I. We define the sequences {z(m)}, {u(m)}, where

In the following way. We put first

If z(m): E c → ℝ, u(m): E c → ℝn are already defined then u (m+1)is a solution of the equation

where

and

The function z(m+1)is given by

We prove that
(I m ) the sequences {z(m)} and {u(m)} are defined on E c and for m ≥ 0, we have

(II m ) there exist the sequences {∂ x z(m)} and for m ≥ 0 we have

We prove (I m ), (II m ) by induction. It is easily seen that conditions (I0), (II0) are satisfied. Suppose that (I m ) and (II m ) hold for a given m ≥ 0. We first prove that there is u(m+1): E c → ℝn, and u(m+1)∈ C∂ψ.c[χ, h]. We claim that

Indeed, it follows from Assumption H[F] and from (44), (45) that for v ∈ C∂ψ.cwe have

and consequently

It follows easily that

From the above estimates and from (44), we deduce (47).
There is  such that for v,
such that for v,  , we have
, we have

For the above v,  we put
we put

Then, we have

and consequently

If follows from the Banach fixed point theorem that there is u(m+1)∈ C∂ψ.c[χ, h] and it is unique.
Then u(m+1)is defined E c . It follows from Assumption H[F] and from (I m ) that

and

We conclude from the above estimates that z(m+1)∈ C∂ψ.c[ζ, d] which completes the proof of (IIm+1).
Put

It follows easily that there is C⋆ ∈ ℝ+ such that

We conclude from (48) that there exist the derivatives ∂ x z(m+1)and

This proves (IIm+1).
II. We prove that the sequences {z(m)} and {u(m)} are uniformly convergent on E c .
It follows from (43)-(46) that there are K0, 

and

where t ∈ [0, c]. From (50) and from the Gronwall inequality, we deduce that there is  such that
such that

Write

It follows from (49), (51) that there is  such that
such that

Set

We conclude from (52) that

and consequently

There is C1 ∈ ℝ+ such that [|V(1)|] ≤ C1. Then,

and there are

such that

It follows from (II
m
) that there exist the derivatives  , and
, and

III. We prove that  is a solution to (28), (29). We conclude from (46) that the functions
is a solution to (28), (29). We conclude from (46) that the functions  ,
,  satisfy the relations
satisfy the relations

For a given (t, x) ∈ E∩([0, c] × ℝn) set  . Then
. Then  for
for  . Then relations (53) imply
. Then relations (53) imply

The relations  and
and  are equivalent. By differentiating (54) with respect to τ and by putting again
are equivalent. By differentiating (54) with respect to τ and by putting again  , we find that
, we find that  is a weak solution to (28). Since
is a weak solution to (28). Since  , it follows that initial condition (29) is satisfied.
, it follows that initial condition (29) is satisfied.
IV. Now we prove (42). It follows from (31) - (35) and from Assumption H[F] that there are  such that
such that

and

Hence, there is  such that the integral inequality
such that the integral inequality

is satisfied, We conclude from the Gronwall inequality that estimate (42) is satisfied with

This completes the proof of the theorem.
Remark 4.6. It is easy to see that differential integral equations and equations with deviated variables are particular cases of (28).
Suppose that f: Ω → ℝ is a given function. Let F: Ξ → ℝ be defined by

Then, equation 1 is equivalent to (28). It follows that existence results for (1), (2) can be obtained from Theorem 4.5.
References
Lakshmikantham V, Leela S: Differential and Integral Inequalities. Acadamic Press, New York; 1969.
Szarski J: Differential Inequalities. Polish Scientific Publishers, Warsaw; 1967.
Ladde GS, Lakshmikantham V, Vatsala A: Monotone Iterative Techniques for Nonlinear Differential Equations. Pitmann Advanced Publishing Program, Boston; 1985.
Lakshimkantham V, Vatsala AS: Generalized Quasilinearization for Nonlinear Problems. Kluwer Acadamic Publication, Dordrecht; 1995.
Van TD, Tsuji M, Thai Son ND: The Characteristics method and Its Generalizations for First Order Nonlinear Partial Differential equations. Chapmann and Hall/CRC, Boca Raton, FL; 2000.
Brandi P, Marcelli C: Haar Inequality in hereditary setting and applications. Rend Sem Math Univ Padova 1966, 96: 177–194.
Kamont Z: Hyperbolic Functional Differential Inequalities. Kluwer Acadamic Publishers, Dordrecht; 1999.
Kamont Z: Infinite systems of hyperbolic functional differential inequalities. Nonlinear Anal TMA 2002, 51: 1429–1445. 10.1016/S0362-546X(01)00907-5
Szarski J: Comparison theorems for infinite systems of differential functional equations and strongly coupled infinite systems of first order partial differential equations. Rocky Mt J Math 1980, 10: 237–246.
Bainov D, Kamont Z, Minchev E: On first order impulsive partial differential inequalities. Appl Math Comput 1994, 61: 207–230. 10.1016/0096-3003(94)90048-5
Byszewski L: Finite systems of strong nonlinear differential functional degenerate implicit inequalities with first order partial derivatives. Univ Iagell Acta Math 1992, 29: 77–84.
Kamont Z, Kozieł S: Functional differential inequalities with unbounded delay. Ann Polon Math 2006, 88: 19–37. 10.4064/ap88-1-2
Augustynowicz A, Kamont Z: On Kamke's functions in uniqueness theorems for first order partial differential functional equations. Nonlinear Anal TMA 1990, 14: 837–850. 10.1016/0362-546X(90)90024-B
Topolski K: On the uniqueness of viscosity solutions for first order partial differential functional equations. Ann Plon Math 1994, 59: 65–75.
Topolski K: Classical methods for viscosity solutions of differential-functional inequalities. Nonlinear World 1997, 4: 1–18.
Cinquini S: Sopra i sistemi iperbolici di equazion a derivate parzaili (nonlinear) in piú variabili indipendenti. Ann Mat pura ed appl 1979, 120: 201–214. 10.1007/BF02411944
Cinquini Cibrario M: Sopra una class di sistemi de equazioni nonlineari a derivate parziali in piú variabili indipendenti. Ann mat pura ed appl 1985, 140: 223–253. 10.1007/BF01776851
Puźniakowska-Gałuch E: On the local Cauchy problem for first order partial differential functional equations. Ann Polon Math 2010, 98: 39–61. 10.4064/ap98-1-3
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kamont, Z. Weak solutions of functional differential inequalities with first-order partial derivatives. J Inequal Appl 2011, 15 (2011). https://doi.org/10.1186/1029-242X-2011-15
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-15
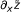 exists on E ∩ ([0, c] ×
exists on E ∩ ([0, c] ×  for t
for t 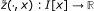 is absolutely continuous,
is absolutely continuous,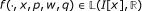
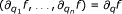 and
and  where (x, p,w,q)
where (x, p,w,q) 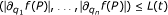 where P = (t, x, p,w, q)
where P = (t, x, p,w, q) 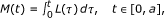
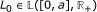 such that
such that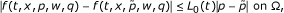
 and
and ,
, 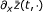 ,
,  ,
,  such
such for t
for t 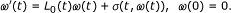
 where (x, w)
where (x, w) 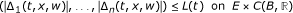
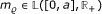 such that ϱ(t, p) ≤ m ϱ(t) for p
such that ϱ(t, p) ≤ m ϱ(t) for p  exist on E and ∂
x
z
exist on E and ∂
x
z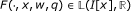
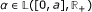 such that
such that
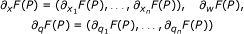
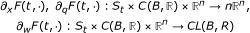
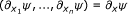 exist on E0 and ∂
x
ψ
exist on E0 and ∂
x
ψ