- Research Article
- Open access
- Published:
Existence results for nonlocal and nonsmooth hemivariational inequalities
Journal of Inequalities and Applications volume 2006, Article number: 79532 (2006)
Abstract
We consider an elliptic hemivariational inequality with nonlocal nonlinearities. Assuming only certain growth conditions on the data, we are able to prove existence results for the problem under consideration. In particular, no continuity assumptions are imposed on the nonlocal term. The proofs rely on a combined use of recent results due to the authors on hemivariational inequalities and operator equations in partially ordered sets.
References
Carl S, Heikkilä S: Nonlinear Differential Equations in Ordered Spaces, Chapman & Hall/CRC Monographs and Surveys in Pure and Applied Mathematics. Volume 111. Chapman & Hall/CRC, Florida; 2000:vi+323.
Carl S, Le VK, Motreanu D: The sub-supersolution method and extremal solutions for quasilinear hemivariational inequalities. Differential Integral Equations 2004,17(1–2):165–178.
Clarke FH: Optimization and Nonsmooth Analysis, Classics in Applied Mathematics. Volume 5. SIAM, Pennsylvania; 1990:xii+308.
Heikkilä S: Existence results for operator equations in partially ordered sets and applications. Nonlinear Analysis 2004,59(7):1033–1044.
Lindqvist P: Addendum: "On the equation
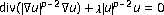 ". Proceedings of the American Mathematical Society 1992,116(2):583–584.
". Proceedings of the American Mathematical Society 1992,116(2):583–584.Naniewicz Z, Panagiotopoulos PD: Mathematical Theory of Hemivariational Inequalities and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 188. Marcel Dekker, New York; 1995:xviii+267.
Zeidler E: Nonlinear Functional Analysis and Its Applications. II/B. Nonlinear Monotone Operators. Springer, New York; 1990.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Carl, S., Heikkilä, S. Existence results for nonlocal and nonsmooth hemivariational inequalities. J Inequal Appl 2006, 79532 (2006). https://doi.org/10.1155/JIA/2006/79532
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/79532
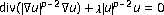 ". Proceedings of the American Mathematical Society 1992,116(2):583–584.
". Proceedings of the American Mathematical Society 1992,116(2):583–584.