- Research Article
- Open access
- Published:
On extrapolation blowups in the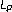
scale
Journal of Inequalities and Applications volume 2006, Article number: 74960 (2006)
Abstract
Yano's extrapolation theorem dated back to 1951 establishes boundedness properties of a subadditive operator
acting continuously in
for
close to
and/or taking
into
as
and/or
with norms blowing up at speed
and/or
,
. Here we give answers in terms of Zygmund, Lorentz-Zygmund and small Lebesgue spaces to what happens if
as
. The study has been motivated by current investigations of convolution maximal functions in stochastic analysis, where the problem occurs for
. We also touch the problem of comparison of results in various scales of spaces.
References
Bennett C, Rudnick K: On Lorentz-Zygmund spaces. Dissertationes Mathematicae (Rozprawy Matematyczne) 1980, 175: 1–67.
Bennett C, Sharpley R: Interpolation of Operators, Pure and Applied Mathematics. Volume 129. Academic Press, Boston; 1988:xiv+469.
Capone C, Fiorenza A: On small Lebesgue spaces. Journal of Function Spaces and Applications 2005,3(1):73–89.
Carro MJ, Martín M: Extrapolation theory for the real interpolation method. Collectanea Mathematica 2002,53(2):165–186.
Da Prato G, Zabczyk J: A note on stochastic convolution. Stochastic Analysis and Applications 1992,10(2):143–153. 10.1080/07362999208809260
Fiorenza A: Duality and reflexivity in grand Lebesgue spaces. Collectanea Mathematica 2000,51(2):131–148.
Fiorenza A, Karadzhov GE: Grand and small Lebesgue spaces and their analogs. Zeitschrift für Analysis und ihre Anwendungen. Journal for Analysis and its Applications 2004,23(4):657–681.
Fiorenza A, Krbec M: On an optimal decomposition in Zygmund spaces. Georgian Mathematical Journal 2002,9(2):271–286.
Fiorenza A, Rakotoson JM: New properties of small Lebesgue spaces and their applications. Mathematische Annalen 2003,326(3):543–561.
Hardy GH, Littlewood JE, Pólya G: Inequalities. 2nd edition. Cambridge University Press, Cambridge; 1952:xii+324.
Iwaniec T, Sbordone C: On the integrability of the Jacobian under minimal hypotheses. Archive for Rational Mechanics and Analysis 1992,119(2):129–143. 10.1007/BF00375119
Krasnosel'skiĭ MA, Rutickiĭ JaB: Convex Functions and Orlicz Spaces. P. Noordhoff, Groningen; 1961:xi+249.
Musielak J: Orlicz Spaces and Modular Spaces, Lecture Notes in Mathematics. Volume 1034. Springer, Berlin; 1983:iii+222.
Rao MM, Ren ZD: Theory of Orlicz Spaces, Monographs and Textbooks in Pure and Applied Mathematics. Volume 146. Marcel Dekker, New York; 1991:xii+449.
Seidler J, Sobukawa T: Exponential integrability of stochastic convolutions. Journal of the London Mathematical Society. Second Series 2003,67(1):245–258. 10.1112/S0024610702003745
Yano S: Notes on Fourier analysis. XXIX. An extrapolation theorem. Journal of the Mathematical Society of Japan 1951, 3: 296–305. 10.2969/jmsj/00320296
Zygmund A: Trigonometric Series. Vols. I, II. 2nd edition. Cambridge University Press, New York; 1959:Vol. I. xii+383 pp.; Vol. II. vii+354.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Capone, C., Fiorenza, A. & Krbec, M. On extrapolation blowups in the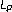
scale.
J Inequal Appl 2006, 74960 (2006). https://doi.org/10.1155/JIA/2006/74960
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/JIA/2006/74960