Skip to main content
Journal of Inequalities and Applications
Download PDF

Essential spectra of quasisimilar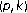-quasihyponormal operators

Journal of Inequalities and Applications volume 2006, Article number: 72641 (2006) Cite this article

Abstract

It is shown that if is an upper-triangular operator matrix acting on the Hilbert space and if denotes the essential spectrum, then the passage from to is accomplished by removing certain open subsets of from the former. Using this result we establish that quasisimilar-quasihyponormal operators have equal spectra and essential spectra.

[1234567891011121314]

References

  1. Clary S: Equality of spectra of quasi-similar hyponormal operators. Proceedings of the American Mathematical Society 1975,53(1):88–90. 10.1090/S0002-9939-1975-0390824-7

    Article  MathSciNet  MATH  Google Scholar 

  2. Douglas RG: On the operator equationand related topics. Acta Scientiarum Mathematicarum (Szeged) 1969, 30: 19–32.

    MathSciNet  MATH  Google Scholar 

  3. Gohberg I, Goldberg S, Kaashoek MA: Classes of Linear Operators. Vol. I, Operator Theory: Advances and Applications. Volume 49. Birkhäuser, Basel; 1990:xiv+468.

    Book  MATH  Google Scholar 

  4. Gupta BC: Quasisimilarity and-quasihyponormal operators. Mathematics Today 1985, 3: 49–54.

    MathSciNet  MATH  Google Scholar 

  5. Han JK, Lee HY, Lee WY: Invertible completions ofupper triangular operator matrices. Proceedings of the American Mathematical Society 2000,128(1):119–123. 10.1090/S0002-9939-99-04965-5

    Article  MathSciNet  MATH  Google Scholar 

  6. Harte RE: Fredholm, Weyl and Browder theory. Proceedings of the Royal Irish Academy. Section A 1985,85(2):151–176.

    MathSciNet  MATH  Google Scholar 

  7. Harte RE: Invertibility and Singularity for Bounded Linear Operators, Monographs and Textbooks in Pure and Applied Mathematics. Volume 109. Marcel Dekker, New York; 1988:xii+590.

    MATH  Google Scholar 

  8. Jeon IH, Lee JI, Uchiyama A: On-quasihyponormal operators and quasisimilarity. Mathematical Inequalities & Applications 2003,6(2):309–315.

    Article  MathSciNet  MATH  Google Scholar 

  9. Kim IH: On-quasihyponormal operators. Mathematical Inequalities & Applications 2004,7(4):629–638.

    Article  MathSciNet  MATH  Google Scholar 

  10. Lee WY: Weyl spectra of operator matrices. Proceedings of the American Mathematical Society 2001,129(1):131–138. 10.1090/S0002-9939-00-05846-9

    Article  MathSciNet  MATH  Google Scholar 

  11. Williams LR: Equality of essential spectra of certain quasisimilar seminormal operators. Proceedings of the American Mathematical Society 1980,78(2):203–209. 10.1090/S0002-9939-1980-0550494-3

    Article  MathSciNet  MATH  Google Scholar 

  12. Williams LR: Equality of essential spectra of quasisimilar quasinormal operators. Journal of Operator Theory 1980,3(1):57–69.

    MathSciNet  MATH  Google Scholar 

  13. Yang LM: Quasisimilarity of hyponormal and subdecomposable operators. Journal of Functional Analysis 1993,112(1):204–217. 10.1006/jfan.1993.1030

    Article  MathSciNet  MATH  Google Scholar 

  14. Yingbin R, Zikun Y: Spectral structure and subdecomposability of-hyponormal operators. Proceedings of the American Mathematical Society 2000,128(7):2069–2074. 10.1090/S0002-9939-99-05257-0

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Changwon National University, Changwon, 641–773, Korea

    An-Hyun Kim

  2. Department of Mathematics, Seoul National University, Seoul, 151-742, Korea

    In Hyoun Kim

Authors
  1. An-Hyun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. In Hyoun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to An-Hyun Kim.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and Permissions

About this article

Cite this article

Kim, AH., Kim, I.H. Essential spectra of quasisimilar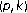-quasihyponormal operators. J Inequal Appl 2006, 72641 (2006). https://doi.org/10.1155/JIA/2006/72641

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/JIA/2006/72641

Keywords

  • Hilbert Space
  • Open Subset
  • Operator Matrix
  • Essential Spectrum
  • Equal Spectrum