- Research Article
- Open access
- Published:
A New Class of Sequences Related to the 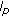 Spaces Defined by Sequences of Orlicz Functions
Spaces Defined by Sequences of Orlicz Functions
Journal of Inequalities and Applications volume 2011, Article number: 539745 (2011)
Abstract
We introduce new sequence space  defined by combining an Orlicz function, seminorms, and
defined by combining an Orlicz function, seminorms, and  -sequences. We study its different properties and obtain some inclusion relation involving the space
-sequences. We study its different properties and obtain some inclusion relation involving the space  Inclusion relation between statistical convergent sequence spaces and Cesaro statistical convergent sequence spaces is also given.
Inclusion relation between statistical convergent sequence spaces and Cesaro statistical convergent sequence spaces is also given.
1. Introduction
By  , we denote the space of all real or complex valued sequences. If
, we denote the space of all real or complex valued sequences. If  , then we simply write
, then we simply write  instead of
instead of  . Also, we will use the conventions that
. Also, we will use the conventions that  . Any vector subspace of
. Any vector subspace of  is called a sequence space. We will write
is called a sequence space. We will write  ,
,  , and
, and  for the sequence spaces of all bounded, convergent, and null sequences, respectively. Further, by
for the sequence spaces of all bounded, convergent, and null sequences, respectively. Further, by  , we denote the sequence space of all
, we denote the sequence space of all  -absolutely convergent series, that is,
-absolutely convergent series, that is,  for
for  . Throughout the article,
. Throughout the article,  ,
,  , and
, and  denote, respectively, the spaces of all, bounded, and
denote, respectively, the spaces of all, bounded, and  -absolutely summable sequences with the elements in
-absolutely summable sequences with the elements in  , where
, where  is a seminormed space. By
is a seminormed space. By  , we denote the zero element in
, we denote the zero element in  .
.  denotes the set of all subsets of
denotes the set of all subsets of  , that do not contain more than
, that do not contain more than  elements. With
elements. With  , we will denote a nondecreasing sequence of positive real numbers such that
, we will denote a nondecreasing sequence of positive real numbers such that  and
and  , as
, as  . The class of all the sequences
. The class of all the sequences  satisfying this property is denoted by
satisfying this property is denoted by  .
.
In paper [1], the notion of  -convergent and bounded sequences is introduced as follows: let
-convergent and bounded sequences is introduced as follows: let  be a strictly increasing sequence of positive reals tending to infinity, that is
be a strictly increasing sequence of positive reals tending to infinity, that is

We say that a sequence  is
is  -convergent to the number
-convergent to the number  , called as the
, called as the  -limit of
-limit of  , if
, if  as
as  , where
, where

In particular, we say that  is a
is a  -null sequence if
-null sequence if  as
as  . Further, we say that
. Further, we say that  is
is  -bounded if
-bounded if  . Here and in the sequel, we will use the convention that any term with a negative subscript is equal to naught, for example,
. Here and in the sequel, we will use the convention that any term with a negative subscript is equal to naught, for example,  and
and  . Now, it is well known [1] that if
. Now, it is well known [1] that if  in the ordinary sense of convergence, then
in the ordinary sense of convergence, then

This implies that

which yields that  and hence
and hence  is
is  -convergent to
-convergent to  . We therefore deduce that the ordinary convergence implies the
. We therefore deduce that the ordinary convergence implies the  -convergence to the same limit.
-convergence to the same limit.
2. Definitions and Background
The space  introduced and studied by Sargent [2] is defined as follows:
introduced and studied by Sargent [2] is defined as follows:

Sargent [2] studied some of its properties and obtained its relationship with the space  . Later on it was investigated from sequence space point of view by Rath [3], Rath and Tripathy [4], Tripathy and Sen [5], Tripathy and Mahanta [6], and others. Lindenstrauss and Tzafriri [7] used the idea of Orlicz function to define the following sequence spaces:
. Later on it was investigated from sequence space point of view by Rath [3], Rath and Tripathy [4], Tripathy and Sen [5], Tripathy and Mahanta [6], and others. Lindenstrauss and Tzafriri [7] used the idea of Orlicz function to define the following sequence spaces:

which is called an Orlicz sequence space. The space  is a Banach space with the norm
is a Banach space with the norm

The space  is closely related to the space
is closely related to the space  which is an Orlicz sequence space with
which is an Orlicz sequence space with  . An Orlicz function is a function
. An Orlicz function is a function  which is continuous, nondecreasing, and convex with
which is continuous, nondecreasing, and convex with  ,
,  for
for  and
and  as
as  . It is well known that if
. It is well known that if  is a convex function and
is a convex function and  , then
, then  for all
for all  with
with  .
.
An Orlicz function  is said to satisfy the
is said to satisfy the  -condition for all values of
-condition for all values of  , if there exists a constant
, if there exists a constant  such that
such that  (see, Krasnoselskii and Rutitsky [8]). In the later stage, different Orlicz sequence spaces were introduced and studied by Bhardwaj and Singh [9], Güngör et al. [10], Tripathy and Mahanta [6], Esi [11], Esi and Et [12], Parashar and Choudhary [13], and many others.
(see, Krasnoselskii and Rutitsky [8]). In the later stage, different Orlicz sequence spaces were introduced and studied by Bhardwaj and Singh [9], Güngör et al. [10], Tripathy and Mahanta [6], Esi [11], Esi and Et [12], Parashar and Choudhary [13], and many others.
The following inequality will be used throughout the paper,

where  and
and  are complex numbers, and
are complex numbers, and  ,
,  . Tripathy and Mahanta [6] defined and studied the following sequence space. Let
. Tripathy and Mahanta [6] defined and studied the following sequence space. Let  be an Orlicz function, then
be an Orlicz function, then

Recently, Altun and Bilgin [14] defined and studied the following sequence spaces:

where  and converges for each
and converges for each  . In this paper, we will define the following sequence spaces:
. In this paper, we will define the following sequence spaces:

3. Results
Since the proofs of the following theorems are not hard we omit them.
Theorem 3.1.
The sequence spaces  are linear spaces over the complex field
are linear spaces over the complex field  .
.
Theorem 3.2.
The space  is a linear topological space paranormed by
is a linear topological space paranormed by

In what follows, we will show inclusion theorems between spaces  .
.
Theorem 3.3.
 if and only if
if and only if

Proof.
Let  and
and  . Then we get
. Then we get

hence  . Conversely, let us suppose that
. Conversely, let us suppose that  and
and  . Then there exists a
. Then there exists a  such that
such that

for every  . Suppose that
. Suppose that  , then there exists a sequence of natural numbers
, then there exists a sequence of natural numbers  such that
such that  . Hence we can write
. Hence we can write

Therefore,  , which is contradiction.
, which is contradiction.
Corollary 3.4.
Let  be an Orlicz function. Then
be an Orlicz function. Then  if and only if
if and only if

Theorem 3.5.
Let  ,
,  ,
,  be Orlicz functions which satisfy the
be Orlicz functions which satisfy the  -condition and
-condition and  , and
, and  seminorms. Then
seminorms. Then
(1) ,
,
(2) ,
,
(3) ,
,
(4)If  is stronger than
is stronger than  , then
, then  , and
, and
(5)If  is equivalent to
is equivalent to  , then
, then  .
.
Proof.
Proof is similar to [14, Theorem 2.5].
Corollary 3.6.
Let  be an Orlicz function which satisfy the
be an Orlicz function which satisfy the  -condition. Then
-condition. Then  .
.
Theorem 3.7.
Let  be a sequence of Orlicz functions. Then the sequence space
be a sequence of Orlicz functions. Then the sequence space  is solid and monotone.
is solid and monotone.
Proof.
Let  , then there exists
, then there exists  such that
such that

for every  . Let
. Let  be a sequence of scalars with
be a sequence of scalars with  for all
for all  . Then from properties of Orlicz functions and seminorm, we get
. Then from properties of Orlicz functions and seminorm, we get

which proves that  is solid space and monotone.
is solid space and monotone.
4. Statistical Convergence
In [15], Fast introduced the idea of statistical convergence. This ideas was later studied by Connor [16], Freedman and Sember [17], and many others. A sequence of positive integers  is called lacunary if
is called lacunary if  , and
, and  as
as  . A sequence
. A sequence  is said to be
is said to be  statistically convergent to
statistically convergent to  if for any
if for any  ,
,

for some  , where
, where  denotes the cardinality of
denotes the cardinality of  . A sequence
. A sequence  is said to be
is said to be  statistically convergent to
statistically convergent to  if for any
if for any  ,
,

for some  .
.
Theorem 4.1.
If  is any Orlicz function,
is any Orlicz function,  strictly increasing sequence, then
strictly increasing sequence, then  .
.
Proof.
Let  . Then
. Then

for every  . Let
. Let  be a sequence of positive numbers. Then it follows that
be a sequence of positive numbers. Then it follows that  is lacunary sequence. Then we get the following relation:
is lacunary sequence. Then we get the following relation:

Taking the limit as  , it follows that
, it follows that  .
.
Theorem 4.2.
If  is any Orlicz bounded function,
is any Orlicz bounded function,  strictly increasing sequence, then
strictly increasing sequence, then  , for every
, for every  .
.
Proof.
Inclusion  , is valid (from Theorem 4.1). In what follows, we will show converse inclusion. Let
, is valid (from Theorem 4.1). In what follows, we will show converse inclusion. Let  , since
, since  is bounded, there exists a constant
is bounded, there exists a constant  such that
such that  . Then for every given
. Then for every given  , we have
, we have

Let us denote by  , as we know this sequence is lacunary and finally we get the following relation:
, as we know this sequence is lacunary and finally we get the following relation:

where the summation  is over
is over  and the summation
and the summation  is over
is over  . Taking the limit as
. Taking the limit as  and
and  , it follows that
, it follows that  .
.
5. Cesaro Convergence
In this paragraph, we will consider that  is a nondecreasing sequence of positive real numbers such that
is a nondecreasing sequence of positive real numbers such that  ,
,  , as
, as  . Let us denote by
. Let us denote by

Theorem 5.1.
If  is an Orlicz function. Then
is an Orlicz function. Then  .
.
Proof.
From the definition of the sequences  , it follows that
, it follows that  . Then there exist a
. Then there exist a  , such that
, such that

Then we get the following relation:

where  . Knowing that
. Knowing that  and
and  are continuous, letting
are continuous, letting  on last relation, we obtain
on last relation, we obtain

Hence  .
.
Theorem 5.2.
Let  . Then for any Orlicz function,
. Then for any Orlicz function,  ,
, .
.
Proof.
Suppose that  , then there exists
, then there exists  such that
such that  for all
for all  . Let
. Let  and
and  , there exist
, there exist  such that for every
such that for every 

We can also find a constant  such that
such that

for all  . Let
. Let  be any integer with
be any integer with  , for every
, for every  . Then
. Then

where  are sets of integer numbers which have more than
are sets of integer numbers which have more than  elements for
elements for  . Passing by limit on last relation, where
. Passing by limit on last relation, where  (since
(since  ,
,  and
and  ), we get that
), we get that

from this, it follows that  .
.
Theorem 5.3.
Let  . Then for any Orlicz function,
. Then for any Orlicz function,  ,
, .
.
References
Mursaleen M, Noman AK: On the spaces of λ -convergent and bounded sequences. Thai Journal of Mathematics 2010,8(2):311–329.
Sargent WLC: Some sequence spaces related to the
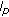 spaces. Journal of the London Mathematical Society 1960, 35: 161–171. 10.1112/jlms/s1-35.2.161
spaces. Journal of the London Mathematical Society 1960, 35: 161–171. 10.1112/jlms/s1-35.2.161Rath D: Spaces of
 -convex sequences and matrix transformations. Indian Journal of Mathematics 1999,41(2):265–280.
-convex sequences and matrix transformations. Indian Journal of Mathematics 1999,41(2):265–280.Rath D, Tripathy BC: Characterization of certain matrix operators. Journal of Orissa Mathematical Society 1989, 8: 121–134.
Tripathy BC, Sen M: On a new class of sequences related to the space
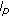 . Tamkang Journal of Mathematics 2002,33(2):167–171.
. Tamkang Journal of Mathematics 2002,33(2):167–171.Tripathy BC, Mahanta S: On a class of sequences related to the
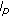 space defined by Orlicz functions. Soochow Journal of Mathematics 2003,29(4):379–391.
space defined by Orlicz functions. Soochow Journal of Mathematics 2003,29(4):379–391.Lindenstrauss J, Tzafriri L: On Orlicz sequence spaces. Israel Journal of Mathematics 1971, 10: 379–390. 10.1007/BF02771656
Krasnoselskii MA, Rutitsky YB: Convex Function and Orlicz Spaces. P.Noordhoff, Groningen, The Netherlands; 1961.
Bhardwaj VK, Singh N: Some sequence spaces defined by Orlicz functions. Demonstratio Mathematica 2000,33(3):571–582.
Güngör M, Et M, Altin Y: Strongly
 -summable sequences defined by Orlicz functions. Applied Mathematics and Computation 2004,157(2):561–571. 10.1016/j.amc.2003.08.051
-summable sequences defined by Orlicz functions. Applied Mathematics and Computation 2004,157(2):561–571. 10.1016/j.amc.2003.08.051Esi A: On a class of new type difference sequence spaces related to the space
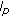 . Far East Journal of Mathematical Sciences 2004,13(2):167–172.
. Far East Journal of Mathematical Sciences 2004,13(2):167–172.Esi A, Et M: Some new sequence spaces defined by a sequence of Orlicz functions. Indian Journal of Pure and Applied Mathematics 2000,31(8):967–973.
Parashar SD, Choudhary B: Sequence spaces defined by Orlicz functions. Indian Journal of Pure and Applied Mathematics 1994,25(4):419–428.
Altun Y, Bilgin T: On a new class of sequences related to the
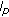 space defined by Orlicz function. Taiwanese Journal of Mathematics 2009,13(4):1189–1196.
space defined by Orlicz function. Taiwanese Journal of Mathematics 2009,13(4):1189–1196.Fast H: Sur la convergence statistique. Colloquium Mathematicum 1951, 2: 241–244.
Connor JS: The statistical and strong
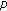 -Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63.
-Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63.Freedman AR, Sember JJ: Densities and summability. Pacific Journal of Mathematics 1981,95(2):293–305.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Braha, N.L. A New Class of Sequences Related to the 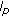 Spaces Defined by Sequences of Orlicz Functions.
J Inequal Appl 2011, 539745 (2011). https://doi.org/10.1155/2011/539745
Spaces Defined by Sequences of Orlicz Functions.
J Inequal Appl 2011, 539745 (2011). https://doi.org/10.1155/2011/539745
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/539745
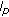 spaces. Journal of the London Mathematical Society 1960, 35: 161–171. 10.1112/jlms/s1-35.2.161
spaces. Journal of the London Mathematical Society 1960, 35: 161–171. 10.1112/jlms/s1-35.2.161 -convex sequences and matrix transformations. Indian Journal of Mathematics 1999,41(2):265–280.
-convex sequences and matrix transformations. Indian Journal of Mathematics 1999,41(2):265–280.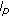 . Tamkang Journal of Mathematics 2002,33(2):167–171.
. Tamkang Journal of Mathematics 2002,33(2):167–171.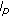 space defined by Orlicz functions. Soochow Journal of Mathematics 2003,29(4):379–391.
space defined by Orlicz functions. Soochow Journal of Mathematics 2003,29(4):379–391. -summable sequences defined by Orlicz functions. Applied Mathematics and Computation 2004,157(2):561–571. 10.1016/j.amc.2003.08.051
-summable sequences defined by Orlicz functions. Applied Mathematics and Computation 2004,157(2):561–571. 10.1016/j.amc.2003.08.051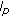 . Far East Journal of Mathematical Sciences 2004,13(2):167–172.
. Far East Journal of Mathematical Sciences 2004,13(2):167–172.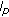 space defined by Orlicz function. Taiwanese Journal of Mathematics 2009,13(4):1189–1196.
space defined by Orlicz function. Taiwanese Journal of Mathematics 2009,13(4):1189–1196.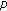 -Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63.
-Cesàro convergence of sequences. Analysis 1988,8(1–2):47–63.