- Research Article
- Open access
- Published:
A Study on the  -Adic
-Adic 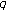 -Integral Representation on
-Integral Representation on 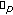 Associated with the Weighted
Associated with the Weighted  -Bernstein and
-Bernstein and 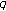 -Bernoulli Polynomials
-Bernoulli Polynomials
Journal of Inequalities and Applications volume 2011, Article number: 513821 (2011)
Abstract
We investigate some interesting properties of the weighted  -Bernstein polynomials related to the weighted
-Bernstein polynomials related to the weighted  -Bernoulli numbers and polynomials by using
-Bernoulli numbers and polynomials by using  -adic
-adic  -integral on
-integral on  .
.
1. Introduction and Preliminaries
Let  be a fixed prime number. Throughout this paper,
be a fixed prime number. Throughout this paper,  ,
,  , and
, and  will denote the ring of
will denote the ring of  -adic integers, the field of
-adic integers, the field of  -adic rational numbers, and the completion of the algebraic closure of
-adic rational numbers, and the completion of the algebraic closure of  , respectively. Let
, respectively. Let  be the set of natural numbers, and let
be the set of natural numbers, and let  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  . Let
. Let  be regarded as either a complex number
be regarded as either a complex number  or a
or a  -adic number
-adic number  . If
. If  , then we always assume
, then we always assume  . If
. If  , we assume that
, we assume that  . In this paper, we define the
. In this paper, we define the  -number as
-number as  (see [1–13]).
(see [1–13]).
Let  be the set of continuous functions on
be the set of continuous functions on  . For
. For  and
and  , the weighted
, the weighted  -Bernstein operator of order
-Bernstein operator of order  for
for  is defined by
is defined by

Here  is called the weighted
is called the weighted  -Bernstein polynomials of degree
-Bernstein polynomials of degree  (see [2, 5, 6]).
(see [2, 5, 6]).
Let  be the space of uniformly differentiable functions on
be the space of uniformly differentiable functions on  . For
. For  , the
, the  -adic
-adic  -integral on
-integral on  , which is called the bosonic
, which is called the bosonic  -integral on
-integral on  , is defined by
, is defined by

(see [10]).
The Carlitz's  -Bernoulli numbers are defined by
-Bernoulli numbers are defined by

with the usual convention about replacing  by
by  (see [3, 9, 10]). In [3], Carlitz also defined the expansion of Carlitz's
(see [3, 9, 10]). In [3], Carlitz also defined the expansion of Carlitz's  -Bernoulli numbers as follows:
-Bernoulli numbers as follows:

with the usual convention about replacing  by
by  .
.
The weighted  -Bernoulli numbers are constructed in previous paper [6] as follows: for
-Bernoulli numbers are constructed in previous paper [6] as follows: for  ,
,

with the usual convention about replacing  by
by  . Let
. Let  . By the definition (1.2) of
. By the definition (1.2) of  -adic
-adic  -integral on
-integral on  , we easily get
, we easily get

Continuing this process, we obtain easily the relation

where  and
and  (see [6]).
(see [6]).
Then by (1.2), applying to the function  , we can see that
, we can see that

The weighted  -Bernoulli polynomials are also defined by the generating function as follows:
-Bernoulli polynomials are also defined by the generating function as follows:

(see[6]). Thus, we note that

From (1.2) and the previous equalities, we obtain the Witt's formula for the weighted  -Bernoulli polynomials as follows:
-Bernoulli polynomials as follows:

By using (1.2) and the weighted  -Bernoulli polynomials, we easily get
-Bernoulli polynomials, we easily get

where  and
and  (see [6]).
(see [6]).
In this paper, we consider the weighted  -Bernstein polynomials to express the bosonic
-Bernstein polynomials to express the bosonic  -integral on
-integral on  and investigate some properties of the weighted
and investigate some properties of the weighted  -Bernstein polynomials associated with the weighted
-Bernstein polynomials associated with the weighted  -Bernoulli polynomials by using the expression of
-Bernoulli polynomials by using the expression of  -adic
-adic  -integral on
-integral on  of those polynomials.
of those polynomials.
2. Weighted 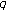 -Bernstein Polynomials and
-Bernstein Polynomials and  -Bernoulli Polynomials
-Bernoulli Polynomials
In this section, we assume that  and
and  with
with  .
.
Now we consider the  -adic weighted
-adic weighted  -Bernstein operator as follows:
-Bernstein operator as follows:

The  -adic
-adic  -Bernstein polynomials with weight
-Bernstein polynomials with weight  of degree
of degree  are given by
are given by

where  ,
,  , and
, and  (see [6, 7]). Note that
(see [6, 7]). Note that  . That is, the weighted
. That is, the weighted  -Bernstein polynomials are symmetric.
-Bernstein polynomials are symmetric.
From the definition of the weighted  -Bernoulli polynomials, we have
-Bernoulli polynomials, we have

By the definition of  -adic
-adic  -integral on
-integral on  , we get
, we get

From (2.3) and (2.4), we have

Therefore, we obtain the following lemma.
Lemma 2.1.
For  , one has
, one has

By (2.2), (2.3), and (2.4), we get

Thus, we have

Therefore, by (2.8), we obtain the following proposition.
Proposition 2.2.
For  with
with  , one has
, one has

By using Proposition 2.2 and Lemma 2.1, we obtain the following corollary.
Corollary 2.3.
For  with
with  , one has
, one has


Taking the bosonic  -integral on
-integral on  for one weighted
for one weighted  -Bernstein polynomials in (2.1), we have
-Bernstein polynomials in (2.1), we have

By the symmetry of  -Bernstein polynomials, we get
-Bernstein polynomials, we get

For  , by (2.11) and (2.13), we have
, by (2.11) and (2.13), we have

By comparing the coefficients on the both sides of (2.12) and (2.14), we obtain the following theorem.
Theorem 2.4.
For  with
with  , one has
, one has

In particular, when  , one has
, one has

Let  with
with  . Then we see that
. Then we see that

Therefore, by (2.17), we obtain the following theorem.
Theorem 2.5.
For  with
with  , one has
, one has

For  , we have
, we have

Therefore, by (2.18) and (2.19), we obtain the following theorem.
Theorem 2.6.
For  with
with  , one has
, one has

Furthermore, for  , one has
, one has

By the induction hypothesis, we obtain the following theorem.
Theorem 2.7.
For  and
and  with
with  , one has
, one has

For  , let
, let  with
with  . Then we show that
. Then we show that

Therefore, by Theorem 2.7 and (2.23), we obtain the following theorem.
Theorem 2.8.
For  , let
, let  with
with  . Then one sees that for
. Then one sees that for 

For  , one has
, one has

References
Acikgoz M, Simsek Y: On multiple interpolation functions of the Nörlund-type
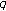 -Euler polynomials. Abstract and Applied Analysis 2009, 2009:-14.
-Euler polynomials. Abstract and Applied Analysis 2009, 2009:-14.Bayad A, Choi J, Kim T, Kim Y-H, Jang LC: -extension of Bernstein polynomials with weighted (;). Journal of Computational and Applied Mathematics. In press
Carlitz L: Expansions of
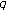 -Bernoulli numbers. Duke Mathematical Journal 1958, 25: 355–364. 10.1215/S0012-7094-58-02532-8
-Bernoulli numbers. Duke Mathematical Journal 1958, 25: 355–364. 10.1215/S0012-7094-58-02532-8Hegazi AS, Mansour M: A note on
 -Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2006,13(1):9–18. 10.2991/jnmp.2006.13.1.2
-Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2006,13(1):9–18. 10.2991/jnmp.2006.13.1.2Jang L-C, Kim W-J, Simsek Y: A study on the
 -adic integral representation on
-adic integral representation on 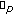 associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6.
associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6.Kim T: On the weighted -Bernoulli numbers and polynomials. http://arxiv.org/abs/1011.5305
Kim T: A note on -Bernstein polynomials. Russian Journal of Mathematical Physics 2011.,18(1):
Kim T: Barnes-type multiple -zeta functions and -Euler polynomials. Journal of Physics A 2010,43(25):-11.
Kim T:
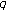 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.Kim T: On a
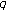 -analogue of the
-analogue of the 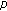 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373Kupershmidt BA: Reflection symmetries of
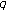 -Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412–422. 10.2991/jnmp.2005.12.s1.34
-Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412–422. 10.2991/jnmp.2005.12.s1.34Ozden H, Cangul IN, Simsek Y: Remarks on
 -Bernoulli numbers associated with Daehee numbers. Advanced Studies in Contemporary Mathematics 2009,18(1):41–48.
-Bernoulli numbers associated with Daehee numbers. Advanced Studies in Contemporary Mathematics 2009,18(1):41–48.Rim S-H, Jin J-H, Moon E-J, Lee S-J: On multiple interpolation functions of the
 -Genocchi polynomials. Journal of Inequalities and Applications 2010, 2010:-13.
-Genocchi polynomials. Journal of Inequalities and Applications 2010, 2010:-13.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, T., Bayad, A. & Kim, YH. A Study on the  -Adic
-Adic 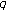 -Integral Representation on
-Integral Representation on 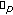 Associated with the Weighted
Associated with the Weighted  -Bernstein and
-Bernstein and 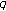 -Bernoulli Polynomials.
J Inequal Appl 2011, 513821 (2011). https://doi.org/10.1155/2011/513821
-Bernoulli Polynomials.
J Inequal Appl 2011, 513821 (2011). https://doi.org/10.1155/2011/513821
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/513821
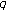 -Bernstein Polynomials and
-Bernstein Polynomials and  -Bernoulli Polynomials
-Bernoulli Polynomials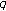 -Euler polynomials. Abstract and Applied Analysis 2009, 2009:-14.
-Euler polynomials. Abstract and Applied Analysis 2009, 2009:-14.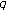 -Bernoulli numbers. Duke Mathematical Journal 1958, 25: 355–364. 10.1215/S0012-7094-58-02532-8
-Bernoulli numbers. Duke Mathematical Journal 1958, 25: 355–364. 10.1215/S0012-7094-58-02532-8 -Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2006,13(1):9–18. 10.2991/jnmp.2006.13.1.2
-Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2006,13(1):9–18. 10.2991/jnmp.2006.13.1.2 -adic integral representation on
-adic integral representation on 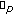 associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6.
associated with Bernstein and Bernoulli polynomials. Advances in Difference Equations 2010, 2010:-6.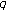 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.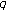 -analogue of the
-analogue of the 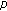 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373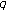 -Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412–422. 10.2991/jnmp.2005.12.s1.34
-Bernoulli polynomials. Journal of Nonlinear Mathematical Physics 2005,12(supplement 1):412–422. 10.2991/jnmp.2005.12.s1.34 -Bernoulli numbers associated with Daehee numbers. Advanced Studies in Contemporary Mathematics 2009,18(1):41–48.
-Bernoulli numbers associated with Daehee numbers. Advanced Studies in Contemporary Mathematics 2009,18(1):41–48. -Genocchi polynomials. Journal of Inequalities and Applications 2010, 2010:-13.
-Genocchi polynomials. Journal of Inequalities and Applications 2010, 2010:-13.