- Research Article
- Open access
- Published:
A Hilbert-Type Integral Inequality in the Whole Plane with the Homogeneous Kernel of Degree −2
Journal of Inequalities and Applications volume 2011, Article number: 401428 (2011)
Abstract
By applying the way of real and complex analysis and estimating the weight functions, we build a new Hilbert-type integral inequality in the whole plane with the homogeneous kernel of degree −2 involving some parameters and the best constant factor. We also consider its reverse. The equivalent forms and some particular cases are obtained.
1. Introduction
If  , satisfying
, satisfying  and
and  , then we have (see [1])
, then we have (see [1])

where the constant factor  is the best possible. Inequality (1.1) is well known as Hilbert's integral inequality, which is important in analysis and in its applications [1, 2]. In recent years, by using the way of weight functions, a number of extensions of (1.1) were given by Yang [3]. Noticing that inequality (1.1) is a Homogenous kernel of degree −1, in 2009, a survey of the study of Hilbert-type inequalities with the homogeneous kernels of degree negative numbers and some parameters is given by [4]. Recently, some inequalities with the homogenous kernels of degree 0 and nonhomogenous kernels have been studied (see [5–9]). All of the above inequalities are built in the quarter plane. Yang [10] built a new Hilbert-type integral inequality in the whole plane as follows:
is the best possible. Inequality (1.1) is well known as Hilbert's integral inequality, which is important in analysis and in its applications [1, 2]. In recent years, by using the way of weight functions, a number of extensions of (1.1) were given by Yang [3]. Noticing that inequality (1.1) is a Homogenous kernel of degree −1, in 2009, a survey of the study of Hilbert-type inequalities with the homogeneous kernels of degree negative numbers and some parameters is given by [4]. Recently, some inequalities with the homogenous kernels of degree 0 and nonhomogenous kernels have been studied (see [5–9]). All of the above inequalities are built in the quarter plane. Yang [10] built a new Hilbert-type integral inequality in the whole plane as follows:

where the constant factor  is the best possible. Zeng and Xie[11] also give a new inequality in the whole plane.
is the best possible. Zeng and Xie[11] also give a new inequality in the whole plane.
By applying the method of [10, 11] and using the way of real and complex analysis, the main objective of this paper is to give a new Hilbert-type integral inequality in the whole plane with the homogeneous kernel of degree −2 involving some parameters and a best constant factor. The reverse form is considered. As applications, we also obtain the equivalent forms and some particular cases.
2. Some Lemmas
Lemma 2.1.
If  ,
,  , define the weight functions
, define the weight functions  and
and  as follow:
as follow:

Then we have  , where
, where

Proof.
For  , setting
, setting  ,
,  , respectively, in the following first and second integrals, we have
, respectively, in the following first and second integrals, we have

Setting a complex function as  , where
, where  and
and  are the first-order poles of
are the first-order poles of  , and
, and  is the first-order zero point of
is the first-order zero point of  , in view of the theorem of obtaining real integral by residue [12], it follows for
, in view of the theorem of obtaining real integral by residue [12], it follows for  that
that

For  , we can find by the integral formula that
, we can find by the integral formula that

Obviously, we find that for  ,
,

Hence we find  .
.
For  , setting
, setting  ,
,  , respectively, in the following first and second integrals, we have
, respectively, in the following first and second integrals, we have

By the same way, we still can find that  . The lemma is proved.
. The lemma is proved.
Note 1.
-
(1)
It is obvious that
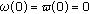 ; (2) If
; (2) If  , then it follows that
, then it follows that 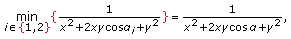 (2.8)
(2.8)
and by Lemma 2.1, we can obtain

Lemma 2.2.
If  ,
,  ,
,  ,
,  , and
, and  is a nonnegative measurable function in
is a nonnegative measurable function in  , then we have
, then we have

Proof.
By Lemma 2.1 and Hölder's inequality [13], we have

Then by Fubini theorem, it follows that

The lemma is proved.
3. Main Results and Applications
Theorem 3.1.
If  ,
,  ,
,  ,
,  , satisfying
, satisfying  and
and  , then we have
, then we have


where the constant factor  and
and  are the best possible and
are the best possible and  is defined by Lemma 2.1. Inequality (3.1) and (3.2) are equivalent.
is defined by Lemma 2.1. Inequality (3.1) and (3.2) are equivalent.
Proof.
If (2.11) takes the form of equality for a  , then there exist constants
, then there exist constants  and
and  , such that they are not all zero, and
, such that they are not all zero, and  a.e. in
a.e. in  . Hence, there exists a constant
. Hence, there exists a constant  , such that
, such that  a.e. in
a.e. in  . We suppose
. We suppose  (otherwise
(otherwise  ). Then
). Then  a. e. in
a. e. in  , which contradicts the fact that
, which contradicts the fact that  . Hence (2.11) takes the form of strict inequality, so does (2.10), and we have (3.2).
. Hence (2.11) takes the form of strict inequality, so does (2.10), and we have (3.2).
By the Hö lder's inequality [13], we have

By (3.2), we have (3.1). On the other hand, suppose that (3.1) is valid. Setting

then it follows  . By (2.10), we have
. By (2.10), we have  . If
. If  , then (3.2) is obvious value; if
, then (3.2) is obvious value; if  , then by (3.1), we obtain
, then by (3.1), we obtain

Hence we have (3.2), which is equivalent to (3.1).
For  , define functions
, define functions  ,
,  as follows:
as follows:

Then  and
and

where

By Fubini theorem [14], we obtain

In view of the above results, if the constant factor  in (3.1) is not the best possible, then exists a positive number
in (3.1) is not the best possible, then exists a positive number  with
with  , such that
, such that

By Fatou lemma [14] and (3.10), we have

which contradicts the fact that  . Hence the constant factor
. Hence the constant factor  in (3.1) is the best possible.
in (3.1) is the best possible.
If the constant factor in (3.2) is not the best possible, then by (3.3), we may get a contradiction that the constant factor in (3.1) is not the best possible. Thus the theorem is proved.
In view of Note (2) and Theorem 3.1, we still have the following theorem.
Theorem 3.2.
If  ,
,  ,
,  ,
,  , and
, and  , satisfying
, satisfying  and
and  , then we have
, then we have

where the constant factors  and
and  are the best possible. Inequality (3.12) is equivalent.
are the best possible. Inequality (3.12) is equivalent.
In particular, for  , we have the following equivalent inequalities:
, we have the following equivalent inequalities:

Theorem 3.3.
As the assumptions of Theorem 3.1, replacing  by
by  , we have the equivalent reverses of (3.1) and (3.2) with the best constant factors.
, we have the equivalent reverses of (3.1) and (3.2) with the best constant factors.
Proof.
By the reverse Hölder's inequality [13], we have the reverse of (2.10) and (3.3). It is easy to obtain the reverse of (3.2). In view of the reverses of (3.2) and (3.3), we obtain the reverse of (3.1). On the other hand, suppose that the reverse of (3.1) is valid. Setting the same  as Theorem 3.1, by the reverse of (2.10), we have
as Theorem 3.1, by the reverse of (2.10), we have  . If
. If  , then the reverse of (3.2) is obvious value; if
, then the reverse of (3.2) is obvious value; if  , then by the reverse of (3.1), we obtain the reverses of (3.5). Hence we have the reverse of (3.2), which is equivalent to the reverse of (3.1).
, then by the reverse of (3.1), we obtain the reverses of (3.5). Hence we have the reverse of (3.2), which is equivalent to the reverse of (3.1).
If the constant factor  in the reverse of (3.1) is not the best possible, then there exists a positive constant
in the reverse of (3.1) is not the best possible, then there exists a positive constant  (with
(with  ), such that the reverse of (3.1) is still valid as we replace
), such that the reverse of (3.1) is still valid as we replace  by
by  . By the reverse of (3.10), we have
. By the reverse of (3.10), we have

For  , by the Levi's theorem [14], we find
, by the Levi's theorem [14], we find

For  ,
,  , such that
, such that  , since
, since

then by Lebesgue control convergence theorem [14], for  , we have
, we have

By (3.14), (3.15), and (3.17), for  , we have
, we have  , which contradicts the fact that
, which contradicts the fact that  . Hence the constant factor
. Hence the constant factor  in the reverse of (3.1) is the best possible.
in the reverse of (3.1) is the best possible.
If the constant factor in reverse of (3.2) is not the best possible, then by the reverse of (3.3), we may get a contradiction that the constant factor in the reverse of (3.1) is not the best possible. Thus the theorem is proved.
By the same way of Theorem 3.3, we still have the following theorem.
Theorem 3.4.
By the assumptions of Theorem 3.2, replacing  by
by  , we have the equivalent reverses of (3.12) with the best constant factors.
, we have the equivalent reverses of (3.12) with the best constant factors.
References
Hardy GH, Littlewood JE, Pólya G: Inequalities. 2nd edition. The University Press, Cambridge, UK; 1952:xii+324.
Mitrinović DS, Pečarić JE, Fink AM: Inequalities Involving Functions and Their Integrals and Derivatives, Mathematics and Its Applications (East European Series). Volume 53. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1991:xvi+587.
Yang B: The Norm of Operator and Hilbert-Type Inequalities. Science Press, Beijing, China; 2009.
Yang BC: A survey of the study of Hilbert-type inequalities with parameters. Advances in Mathematics 2009,38(3):257–268.
Yang BC: On the norm of an integral operator and applications. Journal of Mathematical Analysis and Applications 2006,321(1):182–192. 10.1016/j.jmaa.2005.07.071
Xu J: Hardy-Hilbert's inequalities with two parameters. Advances in Mathematics 2007,36(2):189–202.
Yang BC: On the norm of a Hilbert's type linear operator and applications. Journal of Mathematical Analysis and Applications 2007,325(1):529–541. 10.1016/j.jmaa.2006.02.006
Xin DM: A Hilbert-type integral inequality with a homogeneous kernel of zero degree. Mathematical Theory and Applications 2010,30(2):70–74.
Yang BC: A Hilbert-type integral inequality with a homogeneous kernel of degree zero. Journal of Shandong University. Natural Science 2010,45(2):103–106.
Yang BC: A new Hilbert-type inequality. Bulletin of the Belgian Mathematical Society 2006,13(3):479–487.
Zeng Z, Xie Z: On a new Hilbert-type integral inequality with the integral in whole plane. Journal of Inequalities and Applications 2010, 2010:-8.
Ping Y, Wang H, Song L Jr.: Complex Function. Science Press, Beijing, China; 2004.
Kuang J: Applied Inequalities. Shangdong Science and Technology Press, Jinan, China; 2004.
Kuang J: Introudction to Real Analysis. Hunan Educiton Press, Changsha, China; 1996.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xin, D., Yang, B. A Hilbert-Type Integral Inequality in the Whole Plane with the Homogeneous Kernel of Degree −2. J Inequal Appl 2011, 401428 (2011). https://doi.org/10.1155/2011/401428
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/401428
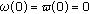 ; (2) If
; (2) If  , then it follows that
, then it follows that