- Research Article
- Open access
- Published:
Jacobi-Sobolev Orthogonal Polynomials: Asymptotics for N-Coherence of Measures
Journal of Inequalities and Applications volume 2011, Article number: 294134 (2011)
Abstract
Let us introduce the Sobolev-type inner product  , where
, where  and
and 
 ,
, 

 , with
, with 
 and
and  for all
for all  A Mehler-Heine-type formula and the inner strong asymptotics on
A Mehler-Heine-type formula and the inner strong asymptotics on  as well as some estimates for the polynomials orthogonal with respect to the above Sobolev inner product are obtained. Necessary conditions for the norm convergence of Fourier expansions in terms of such Sobolev orthogonal polynomials are given.
as well as some estimates for the polynomials orthogonal with respect to the above Sobolev inner product are obtained. Necessary conditions for the norm convergence of Fourier expansions in terms of such Sobolev orthogonal polynomials are given.
1. Introduction
For a nontrivial probability measure  , supported on
, supported on  , we define the linear space
, we define the linear space  of all measurable functions
of all measurable functions  on
on  such that
such that  , where
, where

Let us now introduce the Sobolev-type spaces (see, e.g., [1, Chapter 3] in a more general framework)

where  and
and  ,
,  with
with  ,
,  ,
,  , and
, and  , for all
, for all  . We denote by
. We denote by  the vector of dimension
the vector of dimension  with components
with components  .
.
Let  and
and  in
in  . We can introduce the Sobolev-type inner product
. We can introduce the Sobolev-type inner product

where  and
and


where  ,
,  ,
,  ,
,  , and
, and  , for all
, for all  . In the sequel, we will assume that
. In the sequel, we will assume that  , and, therefore,
, and, therefore,  for all
for all  , and
, and  .
.
Using the standard Gram-Schmidt method for the canonical basis  in the linear space of polynomials, we obtain a unique sequence (up to a constant factor) of polynomials
in the linear space of polynomials, we obtain a unique sequence (up to a constant factor) of polynomials  orthogonal with respect to the above inner product. In the sequel, they will called Jacobi-Sobolev orthogonal polynomials.
orthogonal with respect to the above inner product. In the sequel, they will called Jacobi-Sobolev orthogonal polynomials.
For  and
and  , the pair of measures
, the pair of measures  is a 0-coherent pair, studied in [2–4] (see also [5] in a more general framework). In [6], the authors established the distribution of the zeros of the polynomials orthogonal with respect to the above Sobolev inner product (1.3) when
is a 0-coherent pair, studied in [2–4] (see also [5] in a more general framework). In [6], the authors established the distribution of the zeros of the polynomials orthogonal with respect to the above Sobolev inner product (1.3) when  and
and  . Some results concerning interlacing and separation properties of their zeros with respect to the zeros of Jacobi polynomials are also obtained assuming we are working in a coherent case. More recently, for a noncoherent pair of measures, when
. Some results concerning interlacing and separation properties of their zeros with respect to the zeros of Jacobi polynomials are also obtained assuming we are working in a coherent case. More recently, for a noncoherent pair of measures, when  ,
,  ,
,  , and
, and  , the distribution of zeros of the corresponding Sobolev orthogonal polynomials as well as some asymptotic results (more precisely, inner strong asympttics, outer relative asymptotics, and Mehler-Heine formulas) for these sequences of polynomials are deduced in [7–9]. In the Jacobi case, some analog problems have been considered in [10, 11].
, the distribution of zeros of the corresponding Sobolev orthogonal polynomials as well as some asymptotic results (more precisely, inner strong asympttics, outer relative asymptotics, and Mehler-Heine formulas) for these sequences of polynomials are deduced in [7–9]. In the Jacobi case, some analog problems have been considered in [10, 11].
The aim of this contribution is to study necessary conditions for  -norm convergence of the Fourier expansion in terms of Jacobi-Sobolev orthogonal polynomials. In order to prove it, we need some estimates and strong asymptotics for the polynomials
-norm convergence of the Fourier expansion in terms of Jacobi-Sobolev orthogonal polynomials. In order to prove it, we need some estimates and strong asymptotics for the polynomials  as well as for their derivatives
as well as for their derivatives  . A Mehler-Heine-type formula, inner strong asymptotics, upper bounds in
. A Mehler-Heine-type formula, inner strong asymptotics, upper bounds in  , and
, and  norms of Jacobi-Sobolev orthonormal polynomials are obtained. Thus, we extend the results of [10] for generalized
norms of Jacobi-Sobolev orthonormal polynomials are obtained. Thus, we extend the results of [10] for generalized  -coherent pairs of measures.
-coherent pairs of measures.
The structure of the manuscript is as follows. In Section 2, we give some basic properties of Jacobi polynomials that we will use in the sequel. In Section 3, an algebraic relation between the sequences of polynomials  and Jacobi orthonormal polynomials is stated. It involves
and Jacobi orthonormal polynomials is stated. It involves  (where
(where  ) consecutive terms of such sequences in such a way that we obtain a generalization of the relations satisfied in the coherent case. Upper bounds for the polynomials
) consecutive terms of such sequences in such a way that we obtain a generalization of the relations satisfied in the coherent case. Upper bounds for the polynomials  and their derivatives in
and their derivatives in  are deduced. The inner strong asymptotics as well as a Mehler-Heine-type formula are obtained. Finally, the asymptotic behavior of these polynomials with respect to the
are deduced. The inner strong asymptotics as well as a Mehler-Heine-type formula are obtained. Finally, the asymptotic behavior of these polynomials with respect to the  norm is studied. In Section 4, necessary conditions for the convergence of the Fourier expansions in terms of the sequence of Jacobi-Sobolev orthogonal polynomials are presented.
norm is studied. In Section 4, necessary conditions for the convergence of the Fourier expansions in terms of the sequence of Jacobi-Sobolev orthogonal polynomials are presented.
Throughout this paper, positive constants are denoted by  and they may vary at every occurrence. The notation
and they may vary at every occurrence. The notation  means that the sequence
means that the sequence  converges to 1 and notation
converges to 1 and notation  means
means  for sufficiently large
for sufficiently large  .
.
2. Preliminaries
For  ,
,  , we denote by
, we denote by  the sequence of Jacobi polynomials which are orthonormal on
the sequence of Jacobi polynomials which are orthonormal on  with respect to the inner product
with respect to the inner product

We will denote by  the leading coefficient of any polynomial
the leading coefficient of any polynomial  , and
, and  . Now, we list some properties of the Jacobi orthonormal polynomials which we will use in the sequel.
. Now, we list some properties of the Jacobi orthonormal polynomials which we will use in the sequel.
Proposition 2.1.
-
(a)
The leading coefficient of
 is (see [12, formulas (4.3.4) and (4.21.6)])
is (see [12, formulas (4.3.4) and (4.21.6)])

(b)The derivatives of Jacobi polynomials satisfy (see [12, formula (4.21.7)])

(c)For  , and
, and 

where  if
if  and
and  if
if  (see [12, Theorem 7.32.1]).
(see [12, Theorem 7.32.1]).
(d)For the polynomials  , we get the following estimate (see [12, formula (7.32.6)], [13, Theorem 1]):
, we get the following estimate (see [12, formula (7.32.6)], [13, Theorem 1]):

where  and
and  .
.
(e)Mehler-Heine formula (see [12, Theorem 8.1.1])

where  are real numbers and
are real numbers and  is the Bessel function of the first kind. This formula holds locally uniformly, that is, on every compact subset of the complex plane.
is the Bessel function of the first kind. This formula holds locally uniformly, that is, on every compact subset of the complex plane.
(f)Inner strong asymptotics. For  , when
, when  and
and  , we get (see [12, Theorem 8.21.8])
, we get (see [12, Theorem 8.21.8])

where  ,
,  ,
,  , and
, and  .
.
(g)For  ,
, ,
,  , and
, and  (see [12, p.391. Exercise 91], [14, (2.2)], [15, Theorem 2]),
(see [12, p.391. Exercise 91], [14, (2.2)], [15, Theorem 2]),

Let  be the sequence of orthonormal polynomials with respect to the inner product (1.5), and let
be the sequence of orthonormal polynomials with respect to the inner product (1.5), and let

be the  th polynomial orthonormal with respect to
th polynomial orthonormal with respect to  , where
, where  and
and  ,
,  , are the Tchebychev polynomials of the first kind.
, are the Tchebychev polynomials of the first kind.
Proposition 2.2 ([16, Lemma 2.1]).
For  , there exist constants
, there exist constants  such that
such that

and  , where
, where

Next, we will consider the polynomials

where  ,
,  . Notice that
. Notice that

Taking into account that the zeros of the polynomial  orthogonal with respect to
orthogonal with respect to  on the interval
on the interval  are real, simple, and located in
are real, simple, and located in  , we have
, we have  . Therefore,
. Therefore,  for
for  large enough.
large enough.
On the other hand, using (b) in Proposition 2.1, we have

From Proposition 2.1 and (2.12), we get the following.
Proposition 2.3.
-
(a)
For
 ,
, , and
, and 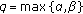 ,
, 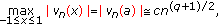 (215)
(215)
where  if
if  and
and  if
if  .
.
-
(b)
When
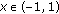 and
and  ,
,  , we get the following estimate for the polynomials
, we get the following estimate for the polynomials  :
: 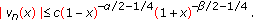 (216)
(216)
-
(c)
Mehler-Heine type formula. We get
 (217)
(217)
where  are real numbers, and
are real numbers, and  is the Bessel function of the first kind. This formula holds locally uniformly, that is, on every compact subset of the complex plane.
is the Bessel function of the first kind. This formula holds locally uniformly, that is, on every compact subset of the complex plane.
-
(d)
Inner strong asymptotics. When
 and
and 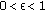 , we get
, we get  (218)
(218)
where  ,
,  ,
,  , and
, and  .
.
-
(e)
For
 ,
,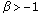 ,
,  , and
, and 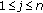 ,
, 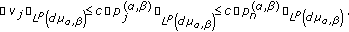 (219)
(219)
3. Asymptotics of Jacobi-Sobolev Orthogonal Polynomials
Let  denote the sequence of polynomials orthogonal with respect to (1.3) normalized by the condition that they have the same leading coefficient as
denote the sequence of polynomials orthogonal with respect to (1.3) normalized by the condition that they have the same leading coefficient as  , that is,
, that is,  .
.
The following relation between  and
and  holds.
holds.
Proposition 3.1.
For  ,
,

where, for  ,
,

Moreover,  and
and  for
for  .
.
Proof.
Expanding  with respect to the basis
with respect to the basis  of the linear space of polynomials with degree at most
of the linear space of polynomials with degree at most  , we get
, we get

where, for  ,
,

For  ,
,

Therefore,

As a conclusion,


Using the extremal property for monic orthogonal polynomials with respect to the corresponding norm (see [12, Theorem 3.1.2]),

we get

Thus,

Finally, from (3.8), we find that

and from Schwarz inequality,

Thus,

Using (3.1) in a recursive way, we get the representation of the polynomial  in terms of the elements of the sequence
in terms of the elements of the sequence  . More precisely we get the following.
. More precisely we get the following.
Proposition 3.2.
For  ,
,  , it holds that
, it holds that

where  ,
,  , and
, and  ,
,  ,
,  . Moreover,
. Moreover,  for
for  , and
, and  for
for  ,
,  .
.
Proof.
Let denote by  ,
,  , and
, and  ,
,  ,
,  . First, we prove that
. First, we prove that

where  , and, by convention,
, and, by convention,  ,
,  .
.
We will prove (3.16) by induction. When  , it is a trivial result. On the other hand, applying (3.1) in a recursive way, we get
, it is a trivial result. On the other hand, applying (3.1) in a recursive way, we get

Taking into account (3.7), we have  . Thus, (3.16) follows for
. Thus, (3.16) follows for  . Now, we assume (3.16) holds for
. Now, we assume (3.16) holds for  . Again, from (3.1),
. Again, from (3.1),

Now, we prove that  for
for  . For
. For  , this follows from (3.7). Since
, this follows from (3.7). Since  and
and  , for
, for  the statement follows by induction. Thus, (3.16) holds for
the statement follows by induction. Thus, (3.16) holds for  . Now taking
. Now taking  in (3.16), we get (3.15).
in (3.16), we get (3.15).
Finally, we prove that  for
for  , and
, and  for
for  ,
,  . First, the following inequality holds:
. First, the following inequality holds:

 . Indeed, for
. Indeed, for  , (3.19) follows from Proposition 3.1 and (3.7). Now, we assume that the relation (3.19) holds for
, (3.19) follows from Proposition 3.1 and (3.7). Now, we assume that the relation (3.19) holds for  . Thus, for
. Thus, for  ,
,

for 

for 

and for 

Therefore, from

the relation (3.19) holds for  . As consequence,
. As consequence,  for
for  and
and  .
.
Now, we will prove by induction that  for
for  and
and  .
.
The case  follows from (3.19). We assume that
follows from (3.19). We assume that  for
for  and
and  . For
. For  ,
,

and for 

Therefore, from

the statement holds for  .
.
Next, we will give some properties of the Jacobi-Sobolev orthogonal polynomials.
Proposition 3.3.
-
(a)
For the polynomials
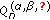 , we get
, we get 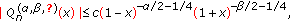 (328)
(328)
where  , and
, and  .
.
-
(b)
For the polynomials
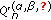 , we get
, we get 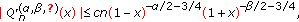 (329)
(329)
where  , and
, and  ,
,  .
.
Proof.
-
(a)
Using Proposition 3.2, we have
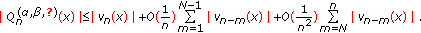 (330)
(330)
Therefore, from Proposition 2.3 , the statement follows immediately.
, the statement follows immediately.
On the other hand, taking into account Proposition 2.1 , Proposition 2.2, (2.14), and (3.15), the proof of
, Proposition 2.2, (2.14), and (3.15), the proof of  can be done in a similar way.
can be done in a similar way.
Now, we show that, like for the classical Jacobi polynomials, the polynomial  attains its maximum in
attains its maximum in  at the end-points. More precisely,
at the end-points. More precisely,
Proposition 3.4.
-
(a)
For
 ,
, 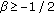 , and
, and 
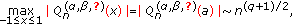 (331)
(331)
where  if
if  and
and  if
if  .
.
-
(b)
For
 ,
,  and
and 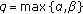
 (332)
(332)
where  if
if  and
and  if
if  .
.
Proof.
Here, we will prove only the case when  . The case when
. The case when  can be done in a similar way.
can be done in a similar way.
-
(a)
From Proposition 2.3
 ,
, 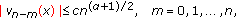 (333)
(333)
for  and
and  . Therefore, according to (3.30),
. Therefore, according to (3.30),

for  and
and  . From Proposition 3.1, we get
. From Proposition 3.1, we get

Finally, from Proposition 2.3(a), the statement follows.
-
(b)
Taking into account Proposition 2.1
 , Proposition 2.2, (2.14), (3.1), and (3.15), we can conclude the proof in the same way as we did in (a).
, Proposition 2.2, (2.14), (3.1), and (3.15), we can conclude the proof in the same way as we did in (a).
Corollary 3.5.
For  ,
,  ,
,

and for  ,
,  ,
,

where

Proof.
The inequality

holds for  , as well as
, as well as

for  . Therefore, from Propositions 3.3 and 3.4, the statement follows immediately.
. Therefore, from Propositions 3.3 and 3.4, the statement follows immediately.
Next, we deduce a Mehler-Heine-type formula for  and
and  (see Theorem 4.1 in [10]).
(see Theorem 4.1 in [10]).
Proposition 3.6.
Uniformly on compact subsets of  ,
,
-
(a)
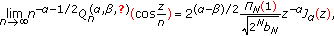 (341)
(341)
-
(b)
 (342)
(342)
where  are real numbers, and
are real numbers, and  is the Bessel function of the first kind.
is the Bessel function of the first kind.
Proof.
To prove the proposition, we use the same technique as in [17].
-
(a)
Multiplying in (3.1) by
 , we obtain
, we obtain 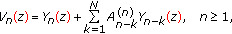 (343)
(343)
where  ,
,  and
and  ,
,  . Moreover,
. Moreover,  and
and  for
for  .
.
Using the above relation in a recursive way as well as the same argument of Proposition 3.2, we have

where  ,
,  for
for  , and
, and  for
for  ,
, . Thus,
. Thus,

On the other hand, from Proposition 2.3(c),  is uniformly bounded on compact subsets of
is uniformly bounded on compact subsets of  . Thus, for a fixed compact set
. Thus, for a fixed compact set  , there exists a constant
, there exists a constant  , depending only on
, depending only on  , such that when
, such that when  ,
,

Thus, the sequence  is uniformly bounded on
is uniformly bounded on  . As a conclusion,
. As a conclusion,

and from Proposition 2.3(c), we obtain the result.
-
(b)
Since we have uniform convergence in (3.41), taking derivatives and using a well known property of Bessel functions of the first kind (see [12, formula 1.71.5]), we obtain (3.42).
Now, we give the inner strong asymptotics of  on
on  .
.
Proposition 3.7.
For  and
and  ,
,


where  ,
,  ,
,  ,
,  , and
, and  .
.
Proof.
From Proposition 3.3(a), the sequence  is uniformly bounded on compact subsets of
is uniformly bounded on compact subsets of  ; thus, from Proposition 3.1,
; thus, from Proposition 3.1,

Now, using Proposition 2.3(d), the relation (3.48) follows.
Concerning (3.49), it can be obtained in a similar way by using Propositions 2.1(f) and 2.2, (2.14), Propositions 3.1 and 3.3(b).
Now, we can give the sharp estimate for the Sobolev norms of the Jacobi-Sobolev polynomials.
Proposition 3.8.
For  and
and  ,
,

Proof.
Clearly, if  , then we get Proposition 3.4(b). Thus, in the proof, we will assume
, then we get Proposition 3.4(b). Thus, in the proof, we will assume  . Since by Proposition 3.2 and(2.14)
. Since by Proposition 3.2 and(2.14)

where  ,
,  , and
, and  are bounded because of the orthonormality condition, we obtain
are bounded because of the orthonormality condition, we obtain

where  , and
, and  .
.
On the other hand, using (3.30), Minkowski's inequality, and Proposition 2.3(e), we deduce

In the same way as above, we get

Thus, from (3.53), (3.54), and (3.55), we have

Notice that the upper estimate in (3.54) and (3.55) can also be proved using the bounds for Jacobi-Sobolev polynomials given in Corollary 3.5.
In order to prove the lower bound in (3.51) we will need the following.
Proposition 3.9.
For  and
and  ,
,

Proof.
We will use a technique similar to [12, Theorem 7.34]. According to (3.42),

On the other hand, from (see [18, Lemma 2.1]), if  and
and  , we have
, we have

Thus, for  and
and  large enough, (3.57) follows.
large enough, (3.57) follows.
Finally, from (3.49), we obtain

The proof of Proposition 3.9 is complete.
From (3.57), for  and
and  ,
,

Thus, using (3.56) and (3.61), the statement follows.
4. Necessary Conditions for the Norm Convergence
The analysis of the norm convergence of partial sums of the Fourier expansions in terms of Jacobi polynomials has been done by many authors. See, for instance, [19–21], and the references therein.
Let  be the Jacobi-Sobolev orthonormal polynomials, that is,
be the Jacobi-Sobolev orthonormal polynomials, that is,

For  , its Fourier expansion in terms of Jacobi-Sobolev orthonormal polynomials is
, its Fourier expansion in terms of Jacobi-Sobolev orthonormal polynomials is

where

Let  be the
be the  th partial sum of the expansion (4.2)
th partial sum of the expansion (4.2)

Theorem 4.1.
Let  , and
, and  . If there exists a constant
. If there exists a constant  such that
such that

for every  , then
, then  with
with

Proof.
For the proof, we apply the same argument as in [20]. Assume that (4.5) holds. Then,

Consider the linear functionals

on  . Hence, for every
. Hence, for every  in
in 
 holds. From the Banach-Steinhaus theorem, this yields
holds. From the Banach-Steinhaus theorem, this yields  . On the other hand, by duality (see, for instance, [1, Theorem 3.8]), we have
. On the other hand, by duality (see, for instance, [1, Theorem 3.8]), we have

where  is the conjugate of
is the conjugate of  . Therefore,
. Therefore,

On the other hand, from (3.51), we obtain the Sobolev norms of Jacobi-Sobolev orthonormal polynomials

for  and
and  . Now, from (4.11), it follows that the inequality (4.10) holds if and only if
. Now, from (4.11), it follows that the inequality (4.10) holds if and only if  .
.
The proof of Theorem 4.1 is complete.
References
Adams RA: Sobolev Spaces, Pure and Applied Mathematics. Volume 6. Academic Press, New York, NY, USA; 1975:xviii+268.
Iserles A, Koch PE, Nørsett SP, Sanz-Serna JM: On polynomials orthogonal with respect to certain Sobolev inner products. Journal of Approximation Theory 1991,65(2):151–175. 10.1016/0021-9045(91)90100-O
Meijer HG: Determination of all coherent pairs. Journal of Approximation Theory 1997,89(3):321–343. 10.1006/jath.1996.3062
Marcellán F, Petronilho J: Orthogonal polynomials and coherent pairs: the classical case. Indagationes Mathematicae 1995,6(3):287–307. 10.1016/0019-3577(95)93197-I
Marcellán F, Martínez-Finkelshtein A, Moreno-Balcázar JJ:
 -coherence of measures with non-classical weights. In Margarita Mathematica de J. J. Guadalupe. Edited by: Español L, Varona JL. Universidad de La Rioja, Logroño, Spain; 2001:77–83.
-coherence of measures with non-classical weights. In Margarita Mathematica de J. J. Guadalupe. Edited by: Español L, Varona JL. Universidad de La Rioja, Logroño, Spain; 2001:77–83.Meijer HG, de Bruin MG: Zeros of Sobolev orthogonal polynomials following from coherent pairs. Journal of Computational and Applied Mathematics 2002,139(2):253–274. 10.1016/S0377-0427(01)00421-6
de Andrade EXL, Bracciali CF, Sri Ranga A: Asymptotics for Gegenbauer-Sobolev orthogonal polynomials associated with non-coherent pairs of measures. Asymptotic Analysis 2008,60(1–2):1–14.
de Andrade EXL, Bracciali CF, Sri Ranga A: Zeros of Gegenbauer-Sobolev orthogonal polynomials: beyond coherent pairs. Acta Applicandae Mathematicae 2009,105(1):65–82. 10.1007/s10440-008-9265-8
Bracciali CF, Castaño-García L, Moreno-Balcázar JJ: Some asymptotics for Sobolev orthogonal polynomials involving Gegenbauer weights. Journal of Computational and Applied Mathematics 2010,235(4):904–915. 10.1016/j.cam.2010.05.028
de Andrade EXL, Bracciali CF, Castaño-García L, Moreno-Balcázar JJ: Asymptotics for Jacobi-Sobolev orthogonal polynomials associated with non-coherent pairs of measures. Journal of Approximation Theory 2010,162(11):1945–1963. 10.1016/j.jat.2010.05.003
de Andrade EXL, Bracciali CF, de Mello MV, Pérez TE: Zeros of Jacobi-Sobolev orthogonal polynomials following non-coherent pair of measures. Computational and Applied Mathematics 2010,29(3):423–445.
Szegő G: Orthogonal Polynomials, American Mathematical Society, Colloquium Publications. Volume 22. 4th edition. American Mathematical Society, Providence, RI, USA; 1975:xiii+432.
Nevai P, Erdélyi T, Magnus AP: Generalized Jacobi weights, Christoffel functions, and Jacobi polynomials. SIAM Journal on Mathematical Analysis 1994,25(2):602–614. 10.1137/S0036141092236863
Markett C: Cohen type inequalities for Jacobi, Laguerre and Hermite expansions. SIAM Journal on Mathematical Analysis 1983,14(4):819–833. 10.1137/0514063
Aptekarev AI, Buyarov VS, Degeza IS: Asymptotic behavior of
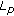 -norms and entropy for general orthogonal polynomials. Russian Academy of Sciences. Sbornik Mathematics 1994,82(2):373–395.
-norms and entropy for general orthogonal polynomials. Russian Academy of Sciences. Sbornik Mathematics 1994,82(2):373–395.Marcellán F, Osilenker BP, Rocha IA: On Fourier-series of a discrete Jacobi-Sobolev inner product. Journal of Approximation Theory 2002,117(1):1–22. 10.1006/jath.2002.3681
Fejzullahu BXh, Marcellán F: Asymptotic properties of orthogonal polynomials with respect to a non-discrete Jacobi-Sobolev inner product. Acta Applicandae Mathematicae 2010,110(3):1309–1320. 10.1007/s10440-009-9511-8
Stempak K: On convergence and divergence of Fourier-Bessel series. Electronic Transactions on Numerical Analysis 2002, 14: 223–235.
Muckenhoupt B: Mean convergence of Jacobi series. Proceedings of the American Mathematical Society 1969, 23: 306–310. 10.1090/S0002-9939-1969-0247360-5
Newman J, Rudin W: Mean convergence of orthogonal series. Proceedings of the American Mathematical Society 1952, 3: 219–222. 10.1090/S0002-9939-1952-0047811-2
Pollard H: The mean convergence of orthogonal series. III. Duke Mathematical Journal 1949, 16: 189–191. 10.1215/S0012-7094-49-01619-1
Acknowledgments
The authors thank the referees for the careful revision of the manuscript. Their comments and suggestions have contributed to improve substantially its presentation. The work of F. Marcellán has been supported by Dirección General de Investigación, Ministerio de Ciencia e Innovación of Spain, Grant no. MTM2009-12740-C03-01.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fejzullahu, B.X., Marcellán, F. Jacobi-Sobolev Orthogonal Polynomials: Asymptotics for N-Coherence of Measures. J Inequal Appl 2011, 294134 (2011). https://doi.org/10.1155/2011/294134
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/294134
 is (see [
is (see [ ,
, , and
, and 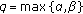 ,
, 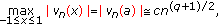
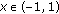 and
and  ,
,  , we get the following estimate for the polynomials
, we get the following estimate for the polynomials  :
: 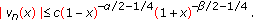

 and
and 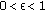 , we get
, we get 
 ,
,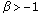 ,
,  , and
, and 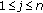 ,
, 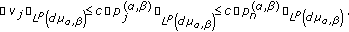
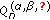 , we get
, we get 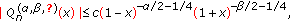
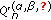 , we get
, we get 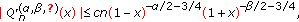
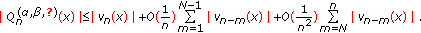
 ,
, 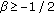 , and
, and 
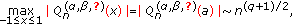
 ,
,  and
and 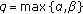

 ,
, 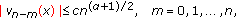
 , Proposition 2.2, (2.14), (3.1), and (3.15), we can conclude the proof in the same way as we did in (a).
, Proposition 2.2, (2.14), (3.1), and (3.15), we can conclude the proof in the same way as we did in (a).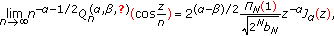

 , we obtain
, we obtain 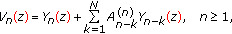
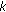 -coherence of measures with non-classical weights. In Margarita Mathematica de J. J. Guadalupe. Edited by: Español L, Varona JL. Universidad de La Rioja, Logroño, Spain; 2001:77–83.
-coherence of measures with non-classical weights. In Margarita Mathematica de J. J. Guadalupe. Edited by: Español L, Varona JL. Universidad de La Rioja, Logroño, Spain; 2001:77–83.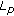 -norms and entropy for general orthogonal polynomials. Russian Academy of Sciences. Sbornik Mathematics 1994,82(2):373–395.
-norms and entropy for general orthogonal polynomials. Russian Academy of Sciences. Sbornik Mathematics 1994,82(2):373–395.