- Research Article
- Open access
- Published:
On the Strong Laws for Weighted Sums of 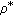 -Mixing Random Variables
-Mixing Random Variables
Journal of Inequalities and Applications volume 2011, Article number: 157816 (2011)
Abstract
Complete convergence is studied for linear statistics that are weighted sums of identically distributed  -mixing random variables under a suitable moment condition. The results obtained generalize and complement some earlier results. A Marcinkiewicz-Zygmund-type strong law is also obtained.
-mixing random variables under a suitable moment condition. The results obtained generalize and complement some earlier results. A Marcinkiewicz-Zygmund-type strong law is also obtained.
1. Introduction
Suppose that  is a sequence of random variables and
is a sequence of random variables and  is a subset of the natural number set
is a subset of the natural number set  . Let
. Let  ,
,

where

Definition 1.1.
A random variable sequence  is said to be a
is said to be a  -mixing random variable sequence if there exists
-mixing random variable sequence if there exists  such that
such that  .
.
The notion of  -mixing seems to be similar to the notion of
-mixing seems to be similar to the notion of  -mixing, but they are quite different from each other. Many useful results have been obtained for
-mixing, but they are quite different from each other. Many useful results have been obtained for  -mixing random variables. For example, Bradley [1] has established the central limit theorem, Byrc and Smoleński [2] and Yang [3] have obtained moment inequalities and the strong law of large numbers, Wu [4, 5], Peligrad and Gut [6], and Gan [7] have studied almost sure convergence, Utev and Peligrad [8] have established maximal inequalities and the invariance principle, An and Yuan [9] have considered the complete convergence and Marcinkiewicz-Zygmund-type strong law of large numbers, and Budsaba et al. [10] have proved the rate of convergence and strong law of large numbers for partial sums of moving average processes based on
-mixing random variables. For example, Bradley [1] has established the central limit theorem, Byrc and Smoleński [2] and Yang [3] have obtained moment inequalities and the strong law of large numbers, Wu [4, 5], Peligrad and Gut [6], and Gan [7] have studied almost sure convergence, Utev and Peligrad [8] have established maximal inequalities and the invariance principle, An and Yuan [9] have considered the complete convergence and Marcinkiewicz-Zygmund-type strong law of large numbers, and Budsaba et al. [10] have proved the rate of convergence and strong law of large numbers for partial sums of moving average processes based on  -mixing random variables under some moment conditions.
-mixing random variables under some moment conditions.
For a sequence  of
of  . random variables, Baum and Katz [11] proved the following well-known complete convergence theorem: suppose that
. random variables, Baum and Katz [11] proved the following well-known complete convergence theorem: suppose that  is a sequence of
is a sequence of  . random variables. Then
. random variables. Then  and
and  if and only if
if and only if  for all
for all  .
.
Hsu and Robbins [12] and Erdös [13] proved the case  and
and  of the above theorem. The case
of the above theorem. The case  and
and  of the above theorem was proved by Spitzer [14]. An and Yuan [9] studied the weighted sums of identically distributed
of the above theorem was proved by Spitzer [14]. An and Yuan [9] studied the weighted sums of identically distributed  -mixing sequence and have the following results.
-mixing sequence and have the following results.
Theorem B.
Let  be a
be a  -mixing sequence of identically distributed random variables,
-mixing sequence of identically distributed random variables,  ,
,  , and suppose that
, and suppose that  for
for  . Assume that
. Assume that  is an array of real numbers satisfying
is an array of real numbers satisfying


If  , then
, then

Theorem C.
Let  be a
be a  -mixing sequence of identically distributed random variables,
-mixing sequence of identically distributed random variables,  ,
,  , and
, and  for
for  . Assume that
. Assume that  is array of real numbers satisfying (1.3). Then
is array of real numbers satisfying (1.3). Then

Recently, Sung [15] obtained the following complete convergence results for weighted sums of identically distributed NA random variables.
Theorem D.
Let  be a sequence of identically distributed NA random variables, and let
be a sequence of identically distributed NA random variables, and let  be an array of constants satisfying
be an array of constants satisfying

for some  . Let
. Let  for some
for some  . Furthermore, suppose that
. Furthermore, suppose that  where
where  . If
. If

then

We find that the proof of Theorem C is mistakenly based on the fact that (1.5) holds for  . Hence, the Marcinkiewicz-Zygmund-type strong laws for
. Hence, the Marcinkiewicz-Zygmund-type strong laws for  -mixing sequence have not been established.
-mixing sequence have not been established.
In this paper, we shall not only partially generalize Theorem D to  -mixing case, but also extend Theorem B to the case
-mixing case, but also extend Theorem B to the case  . The main purpose is to establish the Marcinkiewicz-Zygmund strong laws for linear statistics of
. The main purpose is to establish the Marcinkiewicz-Zygmund strong laws for linear statistics of  -mixing random variables under some suitable conditions.
-mixing random variables under some suitable conditions.
We have the following results.
Theorem 1.2.
Let  be a sequence of identically distributed
be a sequence of identically distributed  -mixing random variables, and let
-mixing random variables, and let  be an array of constants satisfying
be an array of constants satisfying

where  for some
for some  and
and  . Let
. Let  . If
. If  for
for  and (1.8) for
and (1.8) for  , then (1.9) holds.
, then (1.9) holds.
Remark 1.3.
The proof of Theorem D was based on Theorem 1 of Chen et al. [16], which gave sufficient conditions about complete convergence for NA random variables. So far, it is not known whether the result of Chen et al. [16] holds for  -mixing sequence. Hence, we use different methods from those of Sung [15]. We only extend the case
-mixing sequence. Hence, we use different methods from those of Sung [15]. We only extend the case  of Theorem D to
of Theorem D to  -mixing random variables. It is still open question whether the result of Theorem D about the case
-mixing random variables. It is still open question whether the result of Theorem D about the case  holds for
holds for  -mixing sequence.
-mixing sequence.
Theorem 1.4.
Under the conditions of Theorem 1.2, the assumptions  for
for  and (1.8) for
and (1.8) for  imply the following Marcinkiewicz-Zygmund strong law:
imply the following Marcinkiewicz-Zygmund strong law:

2. Proof of the Main Result
Throughout this paper, the symbol  represents a positive constant though its value may change from one appearance to next. It proves convenient to define
represents a positive constant though its value may change from one appearance to next. It proves convenient to define  , where
, where  denotes the natural logarithm.
denotes the natural logarithm.
To obtain our results, the following lemmas are needed.
Lemma 2.1 (Utev and Peligrad [8]).
Suppose  is a positive integer,
is a positive integer,  , and
, and  . Then there exists a positive constant
. Then there exists a positive constant  such that the following statement holds.
such that the following statement holds.
If  is a sequence of random variables such that
is a sequence of random variables such that  with
with  and
and  for every
for every  , then for all
, then for all  ,
,

where  .
.
Lemma 2.2.
Let  be a random variable and
be a random variable and  be an array of constants satisfying (1.10),
be an array of constants satisfying (1.10),  . Then
. Then

Proof.
If  , by
, by  and Lyapounov's inequality, then
and Lyapounov's inequality, then

Hence, (1.7) is satisfied. From the proof of (2.1) of Sung [15], we obtain easily that the result holds.
Proof of Theorem 1.2.
Let  . For all
. For all  , we have
, we have

To obtain (1.9), we need only to prove that  and
and  .
.
By Lemma 2.2, one gets

Before the proof of  , we prove firstly
, we prove firstly

For  ,
,

For  ,
,

Thus (2.6) holds. So, to prove  , it is enough to show that
, it is enough to show that

By the Chebyshev inequality and Lemma 2.1, for  , we have
, we have

For  , we consider the following two cases.
, we consider the following two cases.
If  , note that
, note that  . We have
. We have

If  , note that
, note that  . we have
. we have

Next, we prove  in the following two cases.
in the following two cases.
If  or
or  , take
, take  . Noting that
. Noting that  , we have
, we have

If  or
or  , one gets
, one gets  . Since
. Since  , it implies
, it implies  . Therefore, we have
. Therefore, we have

for all  . Hence,
. Hence,  . Taking
. Taking  , we have
, we have

Proof of Theorem 1.4.
By (1.9), a standard computation (see page 120 of Baum and Katz [11] or page 1472 of An and Yuan [9]), and the Borel-Cantelli Lemma, we have

For any  , there exists an integer
, there exists an integer  such that
such that  . So
. So

From (2.16) and (2.17), we have

References
Bradley RC: On the spectral density and asymptotic normality of weakly dependent random fields. Journal of Theoretical Probability 1992,5(2):355–373. 10.1007/BF01046741
Bryc W, Smoleński W: Moment conditions for almost sure convergence of weakly correlated random variables. Proceedings of the American Mathematical Society 1993,119(2):629–635. 10.1090/S0002-9939-1993-1149969-7
Yang SC: Some moment inequalities for partial sums of random variables and their application. Chinese Science Bulletin 1998,43(17):1823–1828.
Wu QY: Convergence for weighted sums of mixing random sequences. Mathematica Applicata 2002,15(1):1–4.
Wu Q, Jiang Y: Some strong limit theorems for -mixing sequences of random variables. Statistics & Probability Letters 2008,78(8):1017–1023. 10.1016/j.spl.2007.09.061
Peligrad M, Gut A: Almost-sure results for a class of dependent random variables. Journal of Theoretical Probability 1999,12(1):87–104. 10.1023/A:1021744626773
Gan SX: Almost sure convergence for -mixing random variable sequences. Statistics & Probability Letters 2004,67(4):289–298. 10.1016/j.spl.2003.12.011
Utev S, Peligrad M: Maximal inequalities and an invariance principle for a class of weakly dependent random variables. Journal of Theoretical Probability 2003,16(1):101–115. 10.1023/A:1022278404634
An J, Yuan DM: Complete convergence of weighted sums for -mixing sequence of random variables. Statistics & Probability Letters 2008,78(12):1466–1472. 10.1016/j.spl.2007.12.020
Budsaba K, Chen P, Volodin A: Limiting behaviour of moving average processes based on a sequence of mixing and negatively associated random variables. Lobachevskii Journal of Mathematics 2007, 26: 17–25.
Baum LE, Katz M: Convergence rates in the law of large numbers. Transactions of the American Mathematical Society 1965, 120: 108–123. 10.1090/S0002-9947-1965-0198524-1
Hsu PL, Robbins H: Complete convergence and the law of large numbers. Proceedings of the National Academy of Sciences of the United States of America 1947, 33: 25–31. 10.1073/pnas.33.2.25
Erdös P: On a theorem of Hsu and Robbins. Annals of Mathematical Statistics 1949, 20: 286–291. 10.1214/aoms/1177730037
Spitzer F: A combinatorial lemma and its application to probability theory. Transactions of the American Mathematical Society 1956, 82: 323–339. 10.1090/S0002-9947-1956-0079851-X
Sung SH: On the strong convergence for weighted sumsof random variables. Statistical Papers. In press
Chen P, Hu T-C, Liu X, Volodin A: On complete convergence for arrays of rowwise negatively associated random variables. Rossiĭskaya Akademiya Nauk 2007,52(2):393–397.
Acknowledgments
The authors thank the Academic Editor and the reviewers for comments that greatly improved the paper. This work is partially supported by Anhui Provincial Natural Science Foundation (no. 11040606M04), Major Programs Foundation of Ministry of Education of China (no. 309017), National Important Special Project on Science and Technology (2008ZX10005-013), and National Natural Science Foundation of China (11001052, 10971097, and 10871001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhou, XC., Tan, CC. & Lin, JG. On the Strong Laws for Weighted Sums of 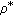 -Mixing Random Variables.
J Inequal Appl 2011, 157816 (2011). https://doi.org/10.1155/2011/157816
-Mixing Random Variables.
J Inequal Appl 2011, 157816 (2011). https://doi.org/10.1155/2011/157816
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/157816