- Research Article
- Open access
- Published:
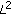 -Error Estimates of the Extrapolated Crank-Nicolson Discontinuous Galerkin Approximations for Nonlinear Sobolev Equations
-Error Estimates of the Extrapolated Crank-Nicolson Discontinuous Galerkin Approximations for Nonlinear Sobolev Equations
Journal of Inequalities and Applications volume 2010, Article number: 895187 (2010)
Abstract
We analyze discontinuous Galerkin methods with penalty terms, namely, symmetric interior penalty Galerkin methods, to solve nonlinear Sobolev equations. We construct finite element spaces on which we develop fully discrete approximations using extrapolated Crank-Nicolson method. We adopt an appropriate elliptic-type projection, which leads to optimal  error estimates of discontinuous Galerkin approximations in both spatial direction and temporal direction.
error estimates of discontinuous Galerkin approximations in both spatial direction and temporal direction.
1. Introduction
Let  be an open bounded domain in
be an open bounded domain in  ,
,  with smooth boundary
with smooth boundary  , and let
, and let  be given. In this paper, we consider the problem of approximating
be given. In this paper, we consider the problem of approximating  satisfying the following nonlinear Sobolev equations:
satisfying the following nonlinear Sobolev equations:

where  denotes the unit outward normal vector to
denotes the unit outward normal vector to  and
and  is a given function defined on
is a given function defined on  . The initial data
. The initial data  ,
,  ,
,  and
and  are assumed to be such that (1.1) admits a solution sufficiently smooth to guarantee the convergence results to be presented below. For details about the physical significance and various properties of existence and uniqueness of the Sobolev equations, see [1–6].
are assumed to be such that (1.1) admits a solution sufficiently smooth to guarantee the convergence results to be presented below. For details about the physical significance and various properties of existence and uniqueness of the Sobolev equations, see [1–6].
Early, in [7–9] the authors constructed the Galerkin approximations to the solution of (1.1) with periodic boundary conditions in one-dimensional space and obtained the optimal convergence in  normed space and superconvergence results. Recently, Lin [10] constructed the Galerkin approximation of (1.1) with
normed space and superconvergence results. Recently, Lin [10] constructed the Galerkin approximation of (1.1) with  using Crank-Nicolson method and proved the optimal convergence of error in
using Crank-Nicolson method and proved the optimal convergence of error in  normed space. In [11] the authors constructed the semidiscrete finite element approximations of (1.1) with nonlinear boundary condition and obtained the optimal
normed space. In [11] the authors constructed the semidiscrete finite element approximations of (1.1) with nonlinear boundary condition and obtained the optimal  -error estimates.
-error estimates.
In this work we will approximate the solution of (1.1) using a discontinuous symmetric Galerkin method with interior penalties for the spatial discretization and extrapolated Crank-Nicolson method for the time stepping. By implementing the extrapolated technique, we induce the linear systems which can be solved explicitly, and thus obviate the order reduction phenomenon which occurs when the system involved is nonlinear.
Compared to the classical Galerkin method, the discontinuous Galerkin method is very well suited for adaptive control of error and can deliver high orders of accuracy when the exact solution is sufficiently smooth. In [12] Rivière and Wheeler formulated and analyzed a family of discontinuous methods to approximate the solution of the transport problem with nonlinear reaction. They construct semidiscrete approximations which converge optimally in  and suboptimally in
and suboptimally in  for the energy norm and suboptimally for the
for the energy norm and suboptimally for the  norm. They also constructed fully discrete approximations and proved the optimal convergence in the temporal direction. Furthermore to solve reactive transport problems Sun and Wheeler in [13] analyzed three discontinuous Galerkin methods, namely, symmetric interior penalty Galerkin method, nonsymmetric interior penalty Galerkin method, and incomplete interior penalty Galerkin method. They obtained error estimates in
norm. They also constructed fully discrete approximations and proved the optimal convergence in the temporal direction. Furthermore to solve reactive transport problems Sun and Wheeler in [13] analyzed three discontinuous Galerkin methods, namely, symmetric interior penalty Galerkin method, nonsymmetric interior penalty Galerkin method, and incomplete interior penalty Galerkin method. They obtained error estimates in  which are optimal in
which are optimal in  and nearly optimal in
and nearly optimal in  and they developed a parabolic lift technique for SIPG which leads to
and they developed a parabolic lift technique for SIPG which leads to  -optimal and nearly
-optimal and nearly  -optimal error estimates in
-optimal error estimates in  and negative norms. Recently in [14, 15] Sun and Yang adapted discontinuous Galerkin methods to nonlinear Sobolev equations and obtained the optimal
and negative norms. Recently in [14, 15] Sun and Yang adapted discontinuous Galerkin methods to nonlinear Sobolev equations and obtained the optimal  error estimates. The main object of this paper is to obtain the optimal
error estimates. The main object of this paper is to obtain the optimal  error estimates in both the spatial direction and the temporal direction by adopting an appropriate elliptic-type projection.
error estimates in both the spatial direction and the temporal direction by adopting an appropriate elliptic-type projection.
This paper is organized as follows. In Section 2, we introduce some notations and preliminaries. In Section 3, we construct appropriate finite element spaces and define an auxiliary projection and prove its convergence. In Section 4, we construct the extrapolated discontinuous Galerkin fully discrete method which yields the second-order convergence in the temporal direction. The corresponding error estimates of the approximate solutions are also discussed.
2. Notations and Preliminaries
Let  be a regular quasi-uniform subdivision of
be a regular quasi-uniform subdivision of  where
where  is a triangle or a quadrilateral if
is a triangle or a quadrilateral if  and
and  is a
is a  -simplex or
-simplex or  -rectangle if
-rectangle if  . Let
. Let  and
and  . Here, the regular requirement is that there exists a constant
. Here, the regular requirement is that there exists a constant  such that each
such that each  contains a ball of radius
contains a ball of radius  . The quasi-uniformity requirement is that there is a constant
. The quasi-uniformity requirement is that there is a constant  such that
such that

We denote the edges (resp., faces for  ) of
) of  by
by  where
where  has positive
has positive  dimensional Lebesgue measure,
dimensional Lebesgue measure,  ,
,  , and
, and  ,
,  . With each edge (or face)
. With each edge (or face)  , we associate a unit normal vector
, we associate a unit normal vector  to
to  if
if  and
and  . For
. For  ,
,  is taken to be the unit outward vector normal to
is taken to be the unit outward vector normal to  .
.
For an  and a domain
and a domain  , we denote by
, we denote by  the Sobolev space of order
the Sobolev space of order  equipped with the usual Sobolev norm
equipped with the usual Sobolev norm  . We simply write
. We simply write  instead of
instead of  if
if  and
and  instead of
instead of  if
if  . And also the usual seminorm defined on
. And also the usual seminorm defined on  is denoted by
is denoted by  .
.
Now for an  and a given subdivision
and a given subdivision  , we define the following space:
, we define the following space:

For  with
with  , we define the average function
, we define the average function  and the jump function
and the jump function  such that
such that

where  with
with  .
.
We associated the following broken norms with the space  :
:

where

is an interior penalty term and  is a discrete positive function that takes the constant value
is a discrete positive function that takes the constant value  on the edge
on the edge  and is bounded below by
and is bounded below by  and above by
and above by  .
.
3. Finite Element Spaces and Convergence of Auxiliary Projection
For a positive integer  , we construct the following finite element spaces:
, we construct the following finite element spaces:

where  denotes the set of polynomials of degree less than or equal to
denotes the set of polynomials of degree less than or equal to  on
on  .
.
Now we state the following  -approximation properties and trace inequalities whose proofs can be found in [16, 17].
-approximation properties and trace inequalities whose proofs can be found in [16, 17].
Lemma 3.1.
Let  and
and  . Then there exist a positive constant
. Then there exist a positive constant  depending on
depending on  ,
,  , and
, and  but independent of
but independent of  ,
,  and
and  and a sequence
and a sequence  ,
,  ,
,  ,
,  such that, for any
such that, for any  ,
,

where  and
and  is an edge or a face of
is an edge or a face of  .
.
Lemma 3.2.
For each  , there exists a positive constant
, there exists a positive constant  depending only on
depending only on  and
and  such that the following trace inequalities hold:
such that the following trace inequalities hold:

where  is an edge or a face of
is an edge or a face of  and
and  is the unit outward normal vector to
is the unit outward normal vector to  .
.
Now we introduce the following bilinear mappings  and
and  defined on
defined on  as
as

Using the bilinear mappings  and
and  , we construct the weak formulation of problem (1.1) as follows:
, we construct the weak formulation of problem (1.1) as follows:

Now for a  we define the following bilinear forms
we define the following bilinear forms  and
and  on
on  such that
such that

 and
and  satisfy the following boundedness and coercivity properties, respectively. The proofs can be found in [18, 19].
satisfy the following boundedness and coercivity properties, respectively. The proofs can be found in [18, 19].
Lemma 3.3.
For a  , there exists a constant
, there exists a constant  satisfying
satisfying

Lemma 3.4.
For a  , there exists a constant
, there exists a constant  satisfying
satisfying

Wheeler [20] introduced an elliptic projection to prove the optimal  -error estimates for Galerkin approximation to parabolic differential equations. Adopting this idea we construct a projection
-error estimates for Galerkin approximation to parabolic differential equations. Adopting this idea we construct a projection  such that
such that

By Lemmas 3.3 and 3.4,  is well defined.
is well defined.
4. The Optimal 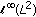 Error Estimates of Fully Discrete Approximations
Error Estimates of Fully Discrete Approximations
In this section we construct fully discrete discontinuous Galerkin approximations using extrapolated Crank-Nicolson method and prove the optimal convergence in  normed space.
normed space.
For a positive integer  we let
we let  and for
and for  and we define
and we define  and
and  . For
. For  , we define
, we define  ,
,  and
and  .
.
The extrapolated Crank-Nicolson discontinuous Galerkin approximation  is defined by
is defined by

where  ,
,  .
.
To apply (4.1), we need two initial stages  and
and  to be defined in the following:
to be defined in the following:

where  .
.
To prove the optimal convergence of  in
in  normed space we denote
normed space we denote  and
and  ,
,  ,
,  ,
,  ,
,  .
.
Now we state the following approximations for  whose proofs can be found in [18, 19].
whose proofs can be found in [18, 19].
Theorem 4.1.
If  and
and  then there exists a constant
then there exists a constant  independent of
independent of  and
and  satisfying
satisfying
(i)
(ii) .
.
Theorem 4.2.
If  ,
,  ,
,  and
and  then there exists a constant
then there exists a constant  independent of
independent of  and
and  satisfying
satisfying
(i)
(ii)
provided that  .
.
By simple computations and the applications of Theorem 4.2 we obtain the following lemmas.
Lemma 4.3.
If  satisfies
satisfies

then there exists a constant  independent of
independent of  and
and  such that
such that

Consequently from Lemma 4.3 there exists a constant  independent of
independent of and
and  such that
such that

if  is sufficiently smooth.
is sufficiently smooth.
Lemma 4.4.
If  then there exists a constant
then there exists a constant  independent of
independent of  and
and  such that
such that

Consequently from Lemma 4.4 there exists a constant  independent of
independent of and
and  such that
such that

if  is sufficiently smooth.
is sufficiently smooth.
Lemma 4.5.
If we let  then there exists a constant
then there exists a constant  independent of
independent of  and
and  such that
such that

Consequently from Lemma 4.5, we induce that there exists a constant  independent of
independent of and
and  such that
such that

if  is sufficiently smooth.
is sufficiently smooth.
Theorem 4.6.
For  and
and  , if
, if  ,
,  then there exists a constant
then there exists a constant  independent of
independent of and
and  such that for
such that for  ,
,  ,
,  ,
, 

hold where  and
and  .
.
Proof.
From (4.1) and (1.1), we have

By the notations of  and
and  , we get
, we get

By the definition of  , we obtain
, we obtain

From the definition of  , we have
, we have

Substituting (4.12)–(4.14) in (4.11) and choosing  imply that
imply that

By Cauchy-Schwarz'sinequality clearly we have

By the definition of  we have
we have

For the definition of  we get
we get

Applying (4.17) and (4.18) in (4.15) we conclude that

For sufficiently small  by applying Lemma 4.3 there exists a constant
by applying Lemma 4.3 there exists a constant  such that
such that

Applying Lemmas 4.3 and 4.4,  can be estimated as follows:
can be estimated as follows:

We obtain the following estimates of  for each
for each 

From the definition of  , we can separate
, we can separate  as follows:
as follows:

By applying Lemma 4.5,  can be estimated in the following way:
can be estimated in the following way:

Similarly there exists a constant  such that
such that

By applying the trace inequality we have

From the estimation of  ,
,  , we have
, we have

By applying Lemma 4.3 we obviously obtain

Now we can separate  as follows:
as follows:

Since

 can be estimated as follows
can be estimated as follows

We apply Lemma 3.2 to estimate  as follows:
as follows:

From the result of approximation of  of Theorem 4.1
of Theorem 4.1

Therefore we get

Similarly,  and
and  are estimated as follows:
are estimated as follows:

Substituting the estimates of  ,
,  into (4.19), we get
into (4.19), we get

If we sum both sides of (4.36) from  to
to  , then we obtain
, then we obtain

which implies

where  is sufficiently small. By applying the discrete version of Gronwall's inequality, we have
is sufficiently small. By applying the discrete version of Gronwall's inequality, we have

Therefore by applying the result of Lemma 4.7 we have

which proves the optimal  error estimation of the fully discrete solutions.
error estimation of the fully discrete solutions.
Lemma 4.7 can be proved by the similar process of Theorem 4.6. as follows
Lemma 4.7.
For  and
and  , if
, if  ,
,  and
and  for some constant
for some constant  then there exists a constant
then there exists a constant  independent of
independent of and
and 

References
Barenblatt GI, Zheltov IP, Kochina IN: Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. Journal of Applied Mathematics and Mechanics 1960, 24(5):1286–1303. 10.1016/0021-8928(60)90107-6
Carroll RW, Showalter RE: Singular and Degenerate Cauchy Problems, Mathematics in Science and Engineering. Volume 127. Academic Press, New York, NY, USA; 1976:viii+333.
Chen PJ, Gurtin ME: On a theory of heat conduction involving two temperatures. Zeitschrift für Angewandte Mathematik und Physik 1968, 19(4):614–627. 10.1007/BF01594969
Davis PL: A quasilinear parabolic and a related third order problem. Journal of Mathematical Analysis and Applications 1972, 40(2):327–335. 10.1016/0022-247X(72)90054-6
Ewing RE: Time-stepping Galerkin methods for nonlinear Sobolev partial differential equations. SIAM Journal on Numerical Analysis 1978, 15(6):1125–1150. 10.1137/0715075
Ting TW: A cooling process according to two-temperature theory of heat conduction. Journal of Mathematical Analysis and Applications 1974, 45: 23–31. 10.1016/0022-247X(74)90116-4
Arnold DN, Douglas, J Jr., Thomée V: Superconvergence of a finite element approximation to the solution of a Sobolev equation in a single space variable. Mathematics of Computation 1981, 36(153):53–63. 10.1090/S0025-5718-1981-0595041-4
Arnold DN: An interior penalty finite element method with discontinuous elements. SIAM Journal on Numerical Analysis 1982, 19(4):742–760. 10.1137/0719052
Nakao MT: Error estimates of a Galerkin method for some nonlinear Sobolev equations in one space dimension. Numerische Mathematik 1985, 47(1):139–157. 10.1007/BF01389881
Lin Y: Galerkin methods for nonlinear Sobolev equations. Aequationes Mathematicae 1990, 40(1):54–66. 10.1007/BF02112280
Lin Y, Zhang T: Finite element methods for nonlinear Sobolev equations with nonlinear boundary conditions. Journal of Mathematical Analysis and Applications 1992, 165(1):180–191. 10.1016/0022-247X(92)90074-N
Rivière B, Wheeler MF: Non conforming methods for transport with nonlinear reaction. In Fluid Flow and Transport in Porous Media: Mathematical and Numerical Treatment, Contemporary Mathematics. Volume 295. American Mathematical Society, Providence, RI, USA; 2002:421–432.
Sun S, Wheeler MF: Symmetric and nonsymmetric discontinuous Galerkin methods for reactive transport in porous media. SIAM Journal on Numerical Analysis 2005, 43(1):195–219. 10.1137/S003614290241708X
Sun T, Yang D: A priori error estimates for interior penalty discontinuous Galerkin method applied to nonlinear Sobolev equations. Applied Mathematics and Computation 2008, 200(1):147–159. 10.1016/j.amc.2007.10.053
Sun T, Yang D: Error estimates for a discontinuous Galerkin method with interior penalties applied to nonlinear Sobolev equations. Numerical Methods for Partial Differential Equations 2008, 24(3):879–896. 10.1002/num.20294
Babuška I, Suri M: The version of the finite element method with quasi-uniform meshes. RAIRO Modélisation Mathématique et Analyse Numérique 1987, 21(2):199–238.
Babuška I, Suri M: The optimal convergence rate of the -version of the finite element method. SIAM Journal on Numerical Analysis 1987, 24(4):750–776. 10.1137/0724049
Ohm MR, Lee HY, Shin JY: Error estimates for discontinuous Galerkin method for nonlinear parabolic equations. Journal of Mathematical Analysis and Applications 2006, 315(1):132–143. 10.1016/j.jmaa.2005.07.027
Ohm MR, Lee HY, Shin JY: -error analysis of discontinuous Galerkin approximations for nonlinear Sobolev equations. submitted
Wheeler MF: A priori error estimates for Galerkin approximations to parabolic partial differential equations. SIAM Journal on Numerical Analysis 1973, 10: 723–759. 10.1137/0710062
Acknowledgment
This research was supported by Dongseo University Research Grants in 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ohm, M., Lee, H. & Shin, J. 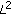 -Error Estimates of the Extrapolated Crank-Nicolson Discontinuous Galerkin Approximations for Nonlinear Sobolev Equations.
J Inequal Appl 2010, 895187 (2010). https://doi.org/10.1155/2010/895187
-Error Estimates of the Extrapolated Crank-Nicolson Discontinuous Galerkin Approximations for Nonlinear Sobolev Equations.
J Inequal Appl 2010, 895187 (2010). https://doi.org/10.1155/2010/895187
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/895187
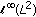 Error Estimates of Fully Discrete Approximations
Error Estimates of Fully Discrete Approximations