- Research Article
- Open access
- Published:
Superstability of Generalized Derivations
Journal of Inequalities and Applications volume 2010, Article number: 740156 (2010)
Abstract
We investigate the superstability of the functional equation  , where
, where  and
and  are the mappings on Banach algebra
are the mappings on Banach algebra  . We have also proved the superstability of generalized derivations associated to the linear functional equation
. We have also proved the superstability of generalized derivations associated to the linear functional equation  , where
, where  .
.
1. Introduction
The well-known problem of stability of functional equations started with a question of Ulam [1] in 1940. In 1941, Ulam's problem was solved by Hyers [2] for Banach spaces. Aoki [3] provided a generalization of Hyers' theorem for approximately additive mappings. In 1978, Rassias [4] generalized Hyers' theorem by obtaining a unique linear mapping near an approximate additive mapping.
Assume that  and
and are real normed spaces with
are real normed spaces with  complete,
complete,  is a mapping such that for each fixed
is a mapping such that for each fixed  the mapping
the mapping  is continuous on
is continuous on  , and there exist
, and there exist  and
and  such that
such that

for all  . Then there exists a unique linear mapping
. Then there exists a unique linear mapping  such that
such that

for all  .
.
In 1994, G vruţa [5] provided a generalization of Rassias' theorem in which he replaced the bound
vruţa [5] provided a generalization of Rassias' theorem in which he replaced the bound  in (1.1) by a general control function
in (1.1) by a general control function  .
.
Since then several stability problems for various functional equations have been investigated by many mathematicians (see [6–8]).
The various problems of the stability of derivations and generalized derivations have been studied during the last few years (see, e.g., [9–18]). The purpose of this paper is to prove the superstability of generalized (ring) derivations on Banach algebras.
The following result which is called the superstability of ring homomorphisms was proved by Bourgin [19] in 1949.
Suppose that  and
and  are Banach algebras and
are Banach algebras and  is with unit. If
is with unit. If  is surjective mapping and there exist
is surjective mapping and there exist  and
and  such that
such that

for all  , then
, then  is a ring homomorphism, that is,
is a ring homomorphism, that is,

The first superstability result concerning derivations between operator algebras was obtained by  emrl in [20]. In [10], Badora proved the superstability of functional equation
emrl in [20]. In [10], Badora proved the superstability of functional equation  where
where  is a mapping on normed algebra
is a mapping on normed algebra  with unit. In Section 2, we generalize Badora's result [10, Theorem
with unit. In Section 2, we generalize Badora's result [10, Theorem  ] for functional equations
] for functional equations


where  and
and  are mappings on algebra
are mappings on algebra  with an approximate identity.
with an approximate identity.
In [21, 22], the superstability of generalized derivations on Banach algebras associated to the following Jensen type functional equation:

where  is an integer is considered. Several authors have studied the stability of the general linear functional equation
is an integer is considered. Several authors have studied the stability of the general linear functional equation

where  ,
,  ,
,  , and
, and  are constants in the field and
are constants in the field and  is a mapping between two Banach spaces (see [23, 24]). In Section 3, we investigate the superstability of generalized (ring) derivations associated to the linear functional equation
is a mapping between two Banach spaces (see [23, 24]). In Section 3, we investigate the superstability of generalized (ring) derivations associated to the linear functional equation

where  . Our results in this section generalize some results of Moslehian's paper [14]. It has been shown by Moslehian [14, Corollary
. Our results in this section generalize some results of Moslehian's paper [14]. It has been shown by Moslehian [14, Corollary  ] that for an approximate generalized derivation
] that for an approximate generalized derivation  on a Banach algebra
on a Banach algebra  , there exists a unique generalized derivation
, there exists a unique generalized derivation  near
near  . We show that the approximate generalized derivation
. We show that the approximate generalized derivation  is a generalized derivation (see Corollary 3.6).
is a generalized derivation (see Corollary 3.6).
Let  be an algebra. An additive map
be an algebra. An additive map  is said to be ring derivation on
is said to be ring derivation on  if
if  for all
for all  . Moreover, if
. Moreover, if  for all
for all  , then
, then  is a derivation. An additive mapping (resp., linear mapping)
is a derivation. An additive mapping (resp., linear mapping)  is called a generalized ring derivation (resp., generalized derivation) if there exists a ring derivation (resp., derivation)
is called a generalized ring derivation (resp., generalized derivation) if there exists a ring derivation (resp., derivation)  such that
such that  for all
for all  .
.
2. Superstability of (1.5) and (1.6)
Here we show the superstability of the functional equations (1.5) and (1.6). We prove the superstability of (1.6) without any additional conditions on the mapping  .
.
Theorem 2.1.
Let  be a normed algebra with a central approximate identity
be a normed algebra with a central approximate identity  and
and  . Suppose that
. Suppose that  and
and  are mappings for which there exists
are mappings for which there exists  such that
such that


for all  . Then
. Then  for all
for all  .
.
Proof.
Replacing  by
by  in (2.2), we get
in (2.2), we get

and so

for all  and
and  . By taking the limit as
. By taking the limit as  , we have
, we have

for all  . Similarly, we have
. Similarly, we have

for all  .
.
Let  and
and  . Then we have
. Then we have

Since  , we get
, we get

By taking the limit as  , we get
, we get

Therefore,  for all
for all  .
.
Theorem 2.2.
Let  be a normed algebra with a left approximate identity and
be a normed algebra with a left approximate identity and  . Let
. Let  and
and  be the mappings satisfying
be the mappings satisfying

for all  , where
, where  is a mapping such that
is a mapping such that

for all  . Then
. Then  for all
for all  .
.
Proof.
Let  . We have
. We have

Replacing  by
by  , we get
, we get

and so

By taking the limit as  , we have
, we have  . Since
. Since  has a left approximate identity, we have
has a left approximate identity, we have  .
.
In the next theorem, we prove the superstability of (1.5) with no additional functional inequality on the mapping  .
.
Theorem 2.3.
Let  be a Banach algebra with a two-sided approximate identity and
be a Banach algebra with a two-sided approximate identity and  . Let
. Let  and
and  be mappings such that
be mappings such that  exists for all
exists for all  and
and

for all  , where
, where  is a function such that
is a function such that

for all  . Then
. Then  ,
,  , and
, and  .
.
Proof.
Replacing  by
by  in (2.15), we get
in (2.15), we get

and so

for all  and
and  . By taking the limit as
. By taking the limit as  , we have
, we have

for all  .
.
Fix  By (2.19), we have
By (2.19), we have

for all  . Then
. Then  for all
for all  and all
and all  , and so by taking the limit as
, and so by taking the limit as  , we have
, we have  . Now we obtain
. Now we obtain  , since
, since  has an approximate identity.
has an approximate identity.
Replacing  by
by  in (2.15), we obtain
in (2.15), we obtain

and hence

for all  and all
and all  . Sending
. Sending  to infinity, we have
to infinity, we have

By (2.23), we get

for all  . Therefore, we have
. Therefore, we have  .
.
The following theorem states the conditions on the mapping  under which the sequence
under which the sequence  converges for all
converges for all  .
.
Theorem 2.4.
Let  be a Banach space and
be a Banach space and  . Suppose that
. Suppose that  is a mapping for which there exists a function
is a mapping for which there exists a function  such that
such that

for all  . Then
. Then  exists and
exists and  for all
for all  .
.
Proof.
3. Superstability of the Generalized Derivations
Our purpose is to prove the superstability of generalized ring derivations and generalized derivations. Throughout this section,  is a Banach algebra with a two-sided approximate identity.
is a Banach algebra with a two-sided approximate identity.
Theorem 3.1.
Let  such that
such that  . Suppose that
. Suppose that  is a mapping with
is a mapping with  for which there exist a map
for which there exist a map  and a function
and a function  such that
such that



for all  . Then
. Then  is a generalized ring derivation and
is a generalized ring derivation and  is a ring derivation. Moreover,
is a ring derivation. Moreover,  for all
for all  .
.
Proof.
Put  and
and  in (3.3). We have
in (3.3). We have  , and so
, and so for all
for all  .
.
Then by (3.2) and applying Theorem 2.4, we have  and
and  for all
for all  .
.
Put  in (3.3). We get
in (3.3). We get

for all  . It follows from (3.1) and Theorem 2.3 that
. It follows from (3.1) and Theorem 2.3 that  ,
,  , and
, and  for all
for all  .
.
It suffices to show that  and
and  are additive.
are additive.
Replacing  by
by  and
and  by
by  and putting
and putting  in (3.3), we obtain
in (3.3), we obtain

and so

for all  and
and  .
.
By taking the limit as  , we get
, we get  , and so
, and so

Putting  and replacing
and replacing  by
by  in (3.7), we have
in (3.7), we have  . Similarly,
. Similarly,  .
.
Replacing  by
by  and
and  by
by  in (3.7), we obtain
in (3.7), we obtain  for all
for all  . Therefore
. Therefore  is an additive mapping.
is an additive mapping.
Since  ,
,  is additive, and
is additive, and  has an approximate identity,
has an approximate identity,  is additive.
is additive.
Theorem 3.2.
Let  such that
such that  . Suppose that
. Suppose that  is a mapping with
is a mapping with  for which there exist a map
for which there exist a map  and a function
and a function  such that
such that



for all  . Then
. Then  is a generalized ring derivation and
is a generalized ring derivation and  is a ring derivation. Moreover,
is a ring derivation. Moreover,  for all
for all  .
.
Proof.
Replacing  ,
,  by
by  and putting
and putting  in (3.10), we get
in (3.10), we get

for all  . Since
. Since

it follows from Theorem 2.4 that  exists for all
exists for all  . By (3.8), we have
. By (3.8), we have

for all  . Putting
. Putting  in (3.10), it follows from Theorem 2.3 that
in (3.10), it follows from Theorem 2.3 that  and
and  for all
for all  and
and  for all
for all  .
.
Replacing  by
by  and
and  by
by  , putting
, putting  in (3.10), and multiplying both sides of the inequality by
in (3.10), and multiplying both sides of the inequality by  , we obtain
, we obtain

for all  and
and  . By taking the limit as
. By taking the limit as  , we get
, we get

for all  . Hence, by the same reasoning as in the proof of Theorem 3.1,
. Hence, by the same reasoning as in the proof of Theorem 3.1,  and
and  are additive mappings. Therefore,
are additive mappings. Therefore,  is a generalized ring derivation and
is a generalized ring derivation and  is a ring derivation.
is a ring derivation.
Remark 3.3.
We note that Theorems 3.1 and 3.2 and all that following results are obtained with no special conditions on the mapping  (see [21, Theorems 2.1 and 2.5]).
(see [21, Theorems 2.1 and 2.5]).
Corollary 3.4.
Let  or
or  ,
,  , and
, and  with
with  . Suppose that
. Suppose that  is a mapping with
is a mapping with  for which there exist a map
for which there exist a map  and
and  such that
such that

for all  . Then
. Then  is a generalized ring derivation and
is a generalized ring derivation and  is a ring derivation.
is a ring derivation.
Proof.
Let  . For
. For  , if
, if  , then
, then  satisfies (3.1), (3.2), and we apply Theorem 3.1, and if
satisfies (3.1), (3.2), and we apply Theorem 3.1, and if  , then we apply Theorem 3.2 since
, then we apply Theorem 3.2 since  has conditions (3.8), (3.9) in this case.
has conditions (3.8), (3.9) in this case.
For  , apply Theorem 3.2 if
, apply Theorem 3.2 if  and apply Theorem 3.1 if
and apply Theorem 3.1 if  .
.
Theorem 3.5.
Let  and let
and let  be a function satisfying either (3.1), (3.2) or (3.8), (3.9). Suppose that
be a function satisfying either (3.1), (3.2) or (3.8), (3.9). Suppose that  is a mapping with
is a mapping with  for which there exists a map
for which there exists a map  such that
such that

for all  and all
and all  . Then
. Then  is a generalized derivation and
is a generalized derivation and  is a derivation.
is a derivation.
Proof.
Let  in (3.17). We have
in (3.17). We have

for all  .
.
Suppose that  satisfies (3.1), (3.2). By Theorem 3.1,
satisfies (3.1), (3.2). By Theorem 3.1,  is a generalized ring derivation and
is a generalized ring derivation and  is a ring derivation. Moreover,
is a ring derivation. Moreover,  for all
for all  .
.
Replacing  by
by  and putting
and putting  in (3.17), we get
in (3.17), we get

for all  ,
,  , and
, and  . Since
. Since  , we obtain
, we obtain

Hence, by taking the limit as  , we get
, we get  for all
for all  and
and  .
.
Let  with
with  . Then
. Then  , and so
, and so

for all  . Now by [21, Lemma 2.4],
. Now by [21, Lemma 2.4],  is a linear mapping and hence
is a linear mapping and hence  is a linear mapping.
is a linear mapping.
The following result generalizes Corollary  and Theorem
and Theorem  of [14].
of [14].
Corollary 3.6.
Let  and
and  with
with  . Suppose that
. Suppose that  is a mapping with
is a mapping with  for which there exist a map
for which there exist a map  and
and  such that
such that

for all  and all
and all  . Then
. Then  is a generalized derivation and
is a generalized derivation and  is a derivation.
is a derivation.
Proof.
Define  and apply Theorem 3.5.
and apply Theorem 3.5.
Theorem 3.7.
Let  and let
and let  be a function satisfying either (3.1), (3.2) or (3.8), (3.9). Suppose that
be a function satisfying either (3.1), (3.2) or (3.8), (3.9). Suppose that  is a mapping with
is a mapping with  for which there exists a map
for which there exists a map  such that
such that

for all  . If
. If  is continuous in
is continuous in  for each fixed
for each fixed  , then
, then  is a generalized derivation and
is a generalized derivation and  is a derivation.
is a derivation.
Proof.
Suppose that  satisfies (3.1), (3.2). By Theorem 3.1,
satisfies (3.1), (3.2). By Theorem 3.1,  is a generalized ring derivation,
is a generalized ring derivation,  is a ring derivation, and
is a ring derivation, and  for all
for all  .
.
Let  . The mapping
. The mapping  , defined by
, defined by  , is continuous in
, is continuous in  . Also, the mapping
. Also, the mapping  is additive, since
is additive, since  is additive. Hence
is additive. Hence  is
is  -linear, and so
-linear, and so

for all  . Therefore,
. Therefore,  is
is  -linear.
-linear.
Now let  . Since
. Since  , there exist
, there exist  such that
such that  . So
. So

for all  . Therefore, the mapping
. Therefore, the mapping  is linear and it follows that
is linear and it follows that  is linear.
is linear.
Corollary 3.8.
Let  or
or  . Suppose that
. Suppose that  is a mapping with
is a mapping with  for which there exists a map
for which there exists a map  such that
such that

for all  . Suppose that
. Suppose that  is continuous in
is continuous in  for each fixed
for each fixed  . Then
. Then  is a generalized derivation and
is a generalized derivation and  is a derivation.
is a derivation.
Proof.
Let  , define
, define  , and apply Theorem 3.7.
, and apply Theorem 3.7.
Theorem 3.9.
Let  be a mapping with
be a mapping with  for which there exist a map
for which there exist a map  and a function
and a function  such that
such that



for  and all
and all  . If
. If  is continuous in
is continuous in  for each fixed
for each fixed  , then
, then  is a generalized derivation and
is a generalized derivation and  is a derivation.
is a derivation.
Proof.
Let  . By Theorem 3.7, it suffices to prove that
. By Theorem 3.7, it suffices to prove that  satisfies (3.1), (3.2).
satisfies (3.1), (3.2).
Let  . We have
. We have

Then  , and so
, and so  . Hence
. Hence  satisfies (3.1).
satisfies (3.1).
Let  . By (3.28), we get
. By (3.28), we get

Hence

and so  satisfies (3.2).
satisfies (3.2).
The theorems similar to Theorem 3.9 have been proved by the assumption that the relations similar to (3.29) are true for  ,
, (see, e.g., [9, 14]). We proved Theorem 3.9, under condition that inequality (3.29) is true for
(see, e.g., [9, 14]). We proved Theorem 3.9, under condition that inequality (3.29) is true for  .
.
References
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1964:xvii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978, 72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994, 184(3):431–436. 10.1006/jmaa.1994.1211
Czerwik S (Ed): Stability of Functional Equations of Ulam-Hyers- Rassias Type. Hadronic Press, Palm Harbor, Fla, USA; 2003.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Rassias ThM (Ed): Functional Equations, Inequalities and Applications. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:x+224.
Amyari M, Rahbarnia F, Sadeghi G: Some results on stability of extended derivations. Journal of Mathematical Analysis and Applications 2007, 329(2):753–758. 10.1016/j.jmaa.2006.07.027
Badora R: On approximate derivations. Mathematical Inequalities & Applications 2006, 9(1):167–173.
Jung Y-S: On the generalized Hyers-Ulam stability of module left derivations. Journal of Mathematical Analysis and Applications 2008, 339(1):108–114. 10.1016/j.jmaa.2007.07.003
Miura T, Hirasawa G, Takahasi S-E: A perturbation of ring derivations on Banach algebras. Journal of Mathematical Analysis and Applications 2006, 319(2):522–530. 10.1016/j.jmaa.2005.06.060
Moslehian MS: Almost derivations on
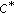 -ternary rings. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007, 14(1):135–142.
-ternary rings. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007, 14(1):135–142.Moslehian MS: Hyers-Ulam-Rassias stability of generalized derivations. International Journal of Mathematics and Mathematical Sciences 2006, 2006:-8.
Moslehian MS: Superstability of higher derivations in multi-Banach algebras. Tamsui Oxford Journal of Mathematical Sciences 2008, 24(4):417–427.
Moslehian MS: Ternary derivations, stability and physical aspects. Acta Applicandae Mathematicae 2008, 100(2):187–199. 10.1007/s10440-007-9179-x
Park C-G: Homomorphisms between
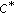 -algebras,
-algebras, 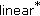 -derivations on a
-derivations on a 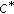 -algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005, 10(5):751–776.
-algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005, 10(5):751–776.Park C-G: Linear derivations on Banach algebras. Nonlinear Functional Analysis and Applications 2004, 9(3):359–368.
Bourgin DG: Approximately isometric and multiplicative transformations on continuous function rings. Duke Mathematical Journal 1949, 16: 385–397. 10.1215/S0012-7094-49-01639-7
Šemrl P: The functional equation of multiplicative derivation is superstable on standard operator algebras. Integral Equations and Operator Theory 1994, 18(1):118–122. 10.1007/BF01225216
Cao H-X, Lv J-R, Rassias JM: Superstability for generalized module left derivations and generalized module derivations on a Banach module (I). Journal of Inequalities and Applications 2009, 2009:-10.
Kang S-Y, Chang I-S: Approximation of generalized left derivations. Abstract and Applied Analysis 2008, 2008:-8.
Grabiec A: The generalized Hyers-Ulam stability of a class of functional equations. Publicationes Mathematicae Debrecen 1996, 48(3–4):217–235.
Jung S-M: On modified Hyers-Ulam-Rassias stability of a generalized Cauchy functional equation. Nonlinear Studies 1998, 5(1):59–67.
Forti G-L: Comments on the core of the direct method for proving Hyers-Ulam stability of functional equations. Journal of Mathematical Analysis and Applications 2004, 295(1):127–133. 10.1016/j.jmaa.2004.03.011
Brzdęk J, Pietrzyk A: A note on stability of the general linear equation. Aequationes Mathematicae 2008, 75(3):267–270. 10.1007/s00010-007-2894-6
Acknowledgment
The authors express their thanks to the referees for their helpful suggestions to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ansari-Piri, E., Anjidani, E. Superstability of Generalized Derivations. J Inequal Appl 2010, 740156 (2010). https://doi.org/10.1155/2010/740156
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/740156
 ] or [
] or [ ].
].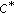 -ternary rings. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007, 14(1):135–142.
-ternary rings. Bulletin of the Belgian Mathematical Society. Simon Stevin 2007, 14(1):135–142.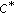 -algebras,
-algebras, 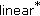 -derivations on a
-derivations on a 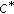 -algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005, 10(5):751–776.
-algebra and the Cauchy-Rassias stability. Nonlinear Functional Analysis and Applications 2005, 10(5):751–776.