- Research Article
- Open access
- Published:
Weighted Inequalities for Potential Operators on Differential Forms
Journal of Inequalities and Applications volume 2010, Article number: 713625 (2010)
Abstract
We develop the weak-type and strong-type inequalities for potential operators under two-weight conditions to the versions of differential forms. We also obtain some estimates for potential operators applied to the solutions of the nonhomogeneous A-harmonic equation.
1. Introduction
In recent years, differential forms as the extensions of functions have been rapidly developed. Many important results have been obtained and been widely used in PDEs, potential theory, nonlinear elasticity theory, and so forth; see [1–3]. In many cases, the process to solve a partial differential equation involves various norm estimates for operators. In this paper, we are devoted to develop some two-weight norm inequalities for potential operator  to the versions of differential forms.
to the versions of differential forms.
We first introduce some notations. Throughout this paper we always use  to denote an open subset of
to denote an open subset of  ,
,  . Assume that
. Assume that  is a ball and
is a ball and  is the ball with the same center as
is the ball with the same center as  and with
and with  . Let
. Let  ,
,  , be the linear space of all
, be the linear space of all  -forms
-forms  with summation over all ordered
with summation over all ordered  -tuples
-tuples  ,
,  . The Grassman algebra
. The Grassman algebra  is a graded algebra with respect to the exterior products
is a graded algebra with respect to the exterior products  . Moreover, if the coefficient
. Moreover, if the coefficient  of
of  -form
-form  is differential on
is differential on  , then we call
, then we call  a differential
a differential  -form on
-form on  and use
and use  to denote the space of all differential
to denote the space of all differential  -forms on
-forms on  . In fact, a differential
. In fact, a differential  -form
-form  is a Schwarz distribution on
is a Schwarz distribution on  with value in
with value in  . For any
. For any  and
and  , the inner product in
, the inner product in  is defined by
is defined by  with summation over all
with summation over all  -tuples
-tuples  and all
and all  . As usual, we still use
. As usual, we still use  to denote the Hodge star operator. Moreover, the norm of
to denote the Hodge star operator. Moreover, the norm of  is given by
is given by  . Also, we use
. Also, we use  to denote the differential operator and use
to denote the differential operator and use  to denote the Hodge codifferential operator defined by
to denote the Hodge codifferential operator defined by  on
on  ,
,  .
.
A weight  is a nonnegative locally integrable function on
is a nonnegative locally integrable function on  . The Lebesgue measure of a set
. The Lebesgue measure of a set  is denoted by
is denoted by  .
.  is a Banach space with norm
is a Banach space with norm

Similarly, for a weight  , we use
, we use  to denote the weighted
to denote the weighted  space with norm
space with norm  .
.
From [1], if  is a differential form defined in a bounded, convex domain
is a differential form defined in a bounded, convex domain  , then there is a decomposition
, then there is a decomposition

where  is called a homotopy operator. Furthermore, we can define the
is called a homotopy operator. Furthermore, we can define the  -form
-form  by
by

for all  ,
,  .
.
For any differential  -form
-form  , we define the potential operator
, we define the potential operator  by
by

where the kernel  is a nonnegative measurable function defined for
is a nonnegative measurable function defined for  and the summation is over all ordered
and the summation is over all ordered  -tuples
-tuples  . It is easy to find that the case
. It is easy to find that the case  reduces to the usual potential operator. That is,
reduces to the usual potential operator. That is,

where  is a function defined on
is a function defined on  . Associated with
. Associated with  , the functional
, the functional  is defined as
is defined as

where  is some sufficiently small constant and
is some sufficiently small constant and  is a ball with radius
is a ball with radius  . Throughout this paper, we always suppose that
. Throughout this paper, we always suppose that  satisfies the following conditions: there exists
satisfies the following conditions: there exists  such that
such that

and there exists  such that
such that

On the potential operator  and the functional
and the functional  , see [4] for details.
, see [4] for details.
For any locally  -integrable form
-integrable form  , the Hardy-Littlewood maximal operator
, the Hardy-Littlewood maximal operator  is defined by
is defined by

where  is the ball of radius
is the ball of radius  , centered at
, centered at  ,
,  .
.
Consider the nonhomogeneous  -harmonic equation for differential forms as follows:
-harmonic equation for differential forms as follows:

where  and
and  are two operators satisfying the conditions
are two operators satisfying the conditions

for almost every  and all
and all  . Here
. Here  are some constants and
are some constants and  is a fixed exponent associated with (1.10). A solution to (1.10) is an element of the Sobolev space
is a fixed exponent associated with (1.10). A solution to (1.10) is an element of the Sobolev space  such that
such that

for all  with compact support. Here
with compact support. Here  are those differential
are those differential  -forms on
-forms on  whose coefficients are in
whose coefficients are in  . The notation
. The notation  is self-explanatory.
is self-explanatory.
2. Weak Type 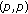 Inequalities for Potential Operators
Inequalities for Potential Operators
In this section, we establish the weighted weaks type  inequalities for potential operators applied to differential forms. To state our results, we need the following definitions and lemmas.
inequalities for potential operators applied to differential forms. To state our results, we need the following definitions and lemmas.
We first need the following generalized Hölder inequality.
Lemma 2.1.
Let  ,
,  , and
, and  . If
. If  and
and  are two measurable functions on
are two measurable functions on  , then
, then

for any  .
.
Definition 2.2.
A pair of weights
 satisfies the
satisfies the
 -condition in a set
-condition in a set
 ; write
; write
 for some
for some
 and
and
 with
with
 if
if

Proposition 2.3.
If  for some
for some  and
and  with
with  , then
, then  satisfies the following condition:
satisfies the following condition:

Proof.
Choose  and
and  . From the Hölder inequality, we have the estimate
. From the Hölder inequality, we have the estimate

Since

we obtain that  satisfies (2.3) as required.
satisfies (2.3) as required.
In [4], Martell proved the following two-weight weak type norm inequality applied to functions.
Lemma 2.4.
Let  and
and  . Assume that
. Assume that  is the potential operator defined in (1.5) and that
is the potential operator defined in (1.5) and that  is a functional satisfying (1.7) and (1.8). Let
is a functional satisfying (1.7) and (1.8). Let  be a pair of weights for which there exists
be a pair of weights for which there exists  such that
such that

Then the potential operator  verifies the following weak type
verifies the following weak type  inequality:
inequality:

where  for any set
for any set  and
and  .
.
The following definition is introduced in [5].
Definition 2.5.
A kernel
 on
on
 satisfies the standard estimates if there exist
satisfies the standard estimates if there exist
 ,
,
 , and constant
, and constant
 such that for all distinct points
such that for all distinct points
 and
and
 in
in
 , and all
, and all
 with
with
 , the kernel
, the kernel
 satisfies
satisfies
 ;
;
 ;
;
 .
.
Theorem 2.6.
Let  be the potential operator defined in (1.4) with the kernel
be the potential operator defined in (1.4) with the kernel  satisfying the condition
satisfying the condition  of the standard estimates and let
of the standard estimates and let  be a differential form in a domain
be a differential form in a domain  . Assume that
. Assume that  satisfies (2.3) for some
satisfies (2.3) for some  and
and  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that the potential operator
, such that the potential operator  satisfies the following weak type
satisfies the following weak type  inequality:
inequality:

where  for any set
for any set  and
and  .
.
Proof.
Since  satisfies condition
satisfies condition  of the standard estimates, for any ball
of the standard estimates, for any ball  of radius
of radius  , we have
, we have

Here  and
and  are two constants independent of
are two constants independent of  . Therefore,
. Therefore,  and
and  are some constants independent of
are some constants independent of  . Thus, from
. Thus, from  satisfying (2.3) for some
satisfying (2.3) for some  and
and  , it follows that
, it follows that

Set  and
and  , where
, where  corresponds to all ordered
corresponds to all ordered  -tuples and
-tuples and  . It is easy to find that there must exist some
. It is easy to find that there must exist some  such that
such that  whenever
whenever  . Since the reverse is obvious, we immediately get
. Since the reverse is obvious, we immediately get  . Thus, using Lemma 2.4 and the elementary inequality
. Thus, using Lemma 2.4 and the elementary inequality  , where
, where  is any constant, we have
is any constant, we have

Combining the above inequality (2.11), the elementary inequality and Lemma 2.4 yield

We complete the proof of Theorem 2.6.
3. The Strong Type 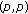 Inequalities for Potential Operators
Inequalities for Potential Operators
In this section, we give the strong type  inequalities for potential operators applied to differential forms. The result in last section shows that
inequalities for potential operators applied to differential forms. The result in last section shows that  -weights are stronger than those of condition (2.3), which is sufficient for the weak
-weights are stronger than those of condition (2.3), which is sufficient for the weak  inequalities, while the following conclusions show that
inequalities, while the following conclusions show that  -condition is sufficient for strong
-condition is sufficient for strong  inequalities.
inequalities.
The following weak reverse Hölder inequality appears in [6].
Lemma 3.1.
Let  ,
,  be a solution of the nonhomogeneous A-harmonic equation in
be a solution of the nonhomogeneous A-harmonic equation in  ,
,  and
and  . Then there exists a constant
. Then there exists a constant  , independent of
, independent of  , such that
, such that

for all balls  with
with  .
.
The following two-weight inequality appears in [7].
Lemma 3.2.
Let  and
and  . Assume that
. Assume that  is the potential operator defined in (1.5) and
is the potential operator defined in (1.5) and  is a functional satisfying (1.7) and (1.8). Let
is a functional satisfying (1.7) and (1.8). Let  be a pair of weights for which there exists
be a pair of weights for which there exists  such that
such that

Then, there exists a constant  , independent of
, independent of  , such that
, such that

Lemma 3.3.
Let  ,
,  ,
,  , be a differential form defined in a domain
, be a differential form defined in a domain  and
and  be the potential operator defined in (1.4) with the kernel
be the potential operator defined in (1.4) with the kernel  satisfying condition
satisfying condition  of standard estimates. Assume that
of standard estimates. Assume that  for some
for some  and
and  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

Proof.
By the proof of Theorem 2.6, note that (3.2) still holds whenever  satisfies the
satisfies the  -condition. Therefore, using Lemma 3.2, we have
-condition. Therefore, using Lemma 3.2, we have

Also, Lemma 3.2 yields that

for all ordered  -tuples
-tuples  . From (3.5) and (3.6), it follows that
. From (3.5) and (3.6), it follows that

We complete the proof of Lemma 3.3.
Lemma 3.3 shows that the two-weight strong  inequality still holds for differential forms. Next, we develop the inequality to the parametric version.
inequality still holds for differential forms. Next, we develop the inequality to the parametric version.
Theorem 3.4.
Let  ,
,  ,
,  , be the solution of the nonhomogeneous A-harmonic equation in a domain
, be the solution of the nonhomogeneous A-harmonic equation in a domain  and let
and let  be the potential operator defined in (1.4) with the kernel
be the potential operator defined in (1.4) with the kernel  satisfying condition
satisfying condition  of standard estimates. Assume that
of standard estimates. Assume that  for some
for some  and
and  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

for all balls  with
with  . Here
. Here  and
and  are constants with
are constants with  .
.
Proof.
Take  . By
. By  , where
, where  and the Hölder inequality, we have
and the Hölder inequality, we have

for all balls  with
with  . Choosing
. Choosing  to be a ball and
to be a ball and  in Lemma 3.3, then there exists a constant
in Lemma 3.3, then there exists a constant  , independent of
, independent of  , such that
, such that

Choosing  and using Lemma 3.1, we obtain
and using Lemma 3.1, we obtain

where  . Combining (3.9), (3.10), and (3.11), it follows that
. Combining (3.9), (3.10), and (3.11), it follows that

Since  , using the Hölder inequality with
, using the Hölder inequality with  , we obtain
, we obtain

From the condition  , we have
, we have

Combining (3.12), (3.13), and (3.14) yields

for all balls  with
with  . Thus, we complete the proof of Theorem 3.4.
. Thus, we complete the proof of Theorem 3.4.
Next, we extend the weighted inequality to the global version, which needs the following lemma about Whitney cover that appears in [6].
Lemma 3.5.
Each open set  has a modified Whitney cover of cubes
has a modified Whitney cover of cubes  such that
such that


for all  and some
and some  , where
, where  is the characteristic function for a set
is the characteristic function for a set  .
.
Theorem 3.6.
Let  ,
,  ,
,  , be the solution of the nonhomogeneous A-harmonic equation in a domain
, be the solution of the nonhomogeneous A-harmonic equation in a domain  and let
and let  be the potential operator defined in (1.4) with the kernel
be the potential operator defined in (1.4) with the kernel  satisfying condition
satisfying condition  of standard estimates. Assume that
of standard estimates. Assume that  for some
for some  and
and  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

where  is some constant with
is some constant with  .
.
Proof.
From Lemma 3.5, we note that  has a modified Whitney cover
has a modified Whitney cover  . Hence, by Theorem 3.4, we have that
. Hence, by Theorem 3.4, we have that

This completes the proof of Theorem 3.6.
Remark 3.7.
Note that if we choose the kernel  to satisfy the standard estimates, then the potential operators
to satisfy the standard estimates, then the potential operators  reduce to the Calderón-Zygmund singular integral operators. Hence, Theorems 3.4 and 3.6 as well as Theorem 2.6 in last section still hold for the Calderón-Zygmund singular integral operators applied to differential forms.
reduce to the Calderón-Zygmund singular integral operators. Hence, Theorems 3.4 and 3.6 as well as Theorem 2.6 in last section still hold for the Calderón-Zygmund singular integral operators applied to differential forms.
4. Applications
In this section, we apply our results to some special operators. We first give the estimate for composite operators. The following lemma appears in [8].
Lemma 4.1.
Let  be the Hardy-Littlewood maximal operator defined in (1.9) and let
be the Hardy-Littlewood maximal operator defined in (1.9) and let  ,
,  ,
,  , be a differential form in a domain
, be a differential form in a domain  . Then,
. Then,  and
and

for some constant  independent of
independent of  .
.
Observing Lemmas 4.1 and 3.3, we immediately have the following estimate for the composition of the Hardy-Littlewood maximal operator  and the potential operator
and the potential operator  .
.
Theorem 4.2.
Let  ,
,  ,
,  , be a differential form defined in a domain
, be a differential form defined in a domain  ,
,  be the Hardy-Littlewood maximal operator defined in (1.9),
be the Hardy-Littlewood maximal operator defined in (1.9),  , and let
, and let  be the potential operator with the kernel
be the potential operator with the kernel  satisfying condition
satisfying condition  of standard estimates. Then, there exists a constant
of standard estimates. Then, there exists a constant  , independent of
, independent of  , such that
, such that

Next, applying our results to some special kernels, we have the following estimates.
Consider that the function  is defined by
is defined by

where  . For any
. For any  , we write
, we write  . It is easy to see that
. It is easy to see that  and
and  . Such functions are called mollifiers. Choosing the kernel
. Such functions are called mollifiers. Choosing the kernel  and setting each coefficient of
and setting each coefficient of  satisfing
satisfing  , we have the following estimate.
, we have the following estimate.
Theorem 4.3.
Let  ,
,  , be a differential form defined in a bounded, convex domain
, be a differential form defined in a bounded, convex domain  , and let
, and let  be coefficient of
be coefficient of  with
with  for all ordered
for all ordered  -tuples
-tuples  . Assume that
. Assume that  and
and  is the potential operator with
is the potential operator with  for any
for any  . Then, there exists a constant
. Then, there exists a constant  , independent of
, independent of  , such that
, such that

Proof.
By the decomposition for differential forms, we have

where  is the homotopy operator. Also, from [1], we have
is the homotopy operator. Also, from [1], we have

for any differential form  defined in
defined in  . Therefore,
. Therefore,

Note that

where the notation  denotes convolution. Hence, we have
denotes convolution. Hence, we have

Since  , it is easy to find that
, it is easy to find that  . Therefore, we have
. Therefore, we have

From (4.7) and (4.10), we obtain

This ends the proof of Theorem 4.3.
References
Agarwal RP, Ding S, Nolder C: Inequalities for Differential Forms. Springer, New York, NY, USA; 2009:xvi+387.
do Carmo MP: Differential Forms and Applications, Universitext. Springer, Berlin, Germany; 1994:x+118.
Warner FW: Foundations of Differentiable Manifolds and Lie Groups, Graduate Texts in Mathematics. Volume 94. Springer, New York, NY, USA; 1983:ix+272.
Martell JM: Fractional integrals, potential operators and two-weight, weak type norm inequalities on spaces of homogeneous type. Journal of Mathematical Analysis and Applications 2004, 294(1):223–236. 10.1016/j.jmaa.2004.02.012
Cruz-Uribe D, Pérez C: Two-weight, weak-type norm inequalities for fractional integrals, Calderón-Zygmund operators and commutators. Indiana University Mathematics Journal 2000, 49(2):697–721.
Nolder CA: Hardy-Littlewood theorems for -harmonic tensors. Illinois Journal of Mathematics 1999, 43(4):613–632.
Sawyer E, Wheeden RL: Weighted inequalities for fractional integrals on Euclidean and homogeneous spaces. American Journal of Mathematics 1992, 114(4):813–874. 10.2307/2374799
Ding S: Norm estimates for the maximal operator and Green's operator. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2009, 16(supplement 1):72–78.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bi, H. Weighted Inequalities for Potential Operators on Differential Forms. J Inequal Appl 2010, 713625 (2010). https://doi.org/10.1155/2010/713625
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/713625
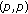 Inequalities for Potential Operators
Inequalities for Potential Operators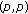 Inequalities for Potential Operators
Inequalities for Potential Operators