- Research Article
- Open access
- Published:
Asymptotic Behavior for a Class of Modified  -Potentials in a Half Space
-Potentials in a Half Space
Journal of Inequalities and Applications volume 2010, Article number: 647627 (2010)
Abstract
A class of  -potentials represented as the sum of modified Green potential and modified Poisson integral are proved to have the growth estimates
-potentials represented as the sum of modified Green potential and modified Poisson integral are proved to have the growth estimates  at infinity in the upper-half space of the
at infinity in the upper-half space of the  -dimensional Euclidean space, where the function
-dimensional Euclidean space, where the function  is a positive non-decreasing function on the interval
is a positive non-decreasing function on the interval  satisfying certain conditions. This result generalizes the growth properties of analytic functions, harmonic functions, and superharmonic functions.
satisfying certain conditions. This result generalizes the growth properties of analytic functions, harmonic functions, and superharmonic functions.
1. Introduction and Main Results
Let 
 denote the
denote the  -dimensional Euclidean space with points
-dimensional Euclidean space with points 
 , where
, where  and
and  . The boundary and closure of an open
. The boundary and closure of an open  of
of  are denoted by
are denoted by  and
and  , respectively. The upper half-space is the set
, respectively. The upper half-space is the set  , whose boundary is
, whose boundary is  . We identify
. We identify  with
with  and
and  with
with  , writing typical points
, writing typical points  as
as  where
where  and putting
and putting 
For  and
and  , let
, let  denote the open ball with center at
denote the open ball with center at  and radius
and radius  in
in  .
.
It is well known that (see, e.g., [1, Chapter 6]) the positive powers of the Laplace operator  can be defined by
can be defined by

where  ,
,  is a Schwarz function and
is a Schwarz function and

It follows that we can extend definition (1.1) to certain negative powers of  ,
,  for
for  and define an operator
and define an operator  by
by

where  and
and  is a function in the Schwartz class.
is a function in the Schwartz class.
If  is defined as the inverse Fourier transform of
is defined as the inverse Fourier transform of  (in the sense of distributions), one can show that
(in the sense of distributions), one can show that

where  is a certain constant (see, e.g., [1, page 414] for the exact value of
is a certain constant (see, e.g., [1, page 414] for the exact value of  ).
).
The function  is known as the Riesz kernel. It follows immediately from the rules for manipulating Fourier transforms that any Schwartz function
is known as the Riesz kernel. It follows immediately from the rules for manipulating Fourier transforms that any Schwartz function  can be written as a Riesz potential,
can be written as a Riesz potential,

where  and
and  .
.
This Riesz kernel  in
in  inspired us to introduce the modified Riesz kernel for
inspired us to introduce the modified Riesz kernel for  . To do this, we first set
. To do this, we first set

Let  be the modified Riesz kernel for
be the modified Riesz kernel for  , that is,
, that is,

where  denotes reflection in the boundary plane
denotes reflection in the boundary plane  just as
just as  .
.
We define the kernel function  when
when  and
and  by
by

where  if
if  and
and  if
if  .
.
We remark that  and
and  are the classical Green function and classical Poisson kernel for
are the classical Green function and classical Poisson kernel for  respectively (see, e.g., [2, page 127]).
respectively (see, e.g., [2, page 127]).
Next we use the following modified kernel function  defined by
defined by

where  is a nonnegative integer;
is a nonnegative integer;  is the ultraspherical (or Gegenbauer) polynomials (see [3]). The Gegenbauer polynomials come from the generating function
is the ultraspherical (or Gegenbauer) polynomials (see [3]). The Gegenbauer polynomials come from the generating function

where  ,
,  , and
, and  . The coefficients
. The coefficients  are called the ultraspherical (or Gegenbauer) polynomials of degree
are called the ultraspherical (or Gegenbauer) polynomials of degree  associated with
associated with  , each function
, each function  is a polynomial of degree
is a polynomial of degree  in
in  . Here note that
. Here note that  is the modified Poisson kernel in
is the modified Poisson kernel in  , which has been used by several authors (see, e.g., [4–8]).
, which has been used by several authors (see, e.g., [4–8]).
Motivated by this modified kernel function  , it is natural to ask if the function
, it is natural to ask if the function  can also be modified? In this paper, we give an affirmative answer to this question.
can also be modified? In this paper, we give an affirmative answer to this question.
First we consider the modified kernel function in case  , which is defined by
, which is defined by

In case  , we define
, we define

where  is a nonnegative integer,
is a nonnegative integer,  , and
, and  .
.
Then we define the modified kernel function  by
by

Write

where  (resp.,
(resp.,  ) is a nonnegative measure on
) is a nonnegative measure on  (resp.,
(resp.,  ). Here note that
). Here note that  is nothing but the Green potential of general order (see [9–11]).
is nothing but the Green potential of general order (see [9–11]).
Following Fuglede (see [6]), we set

for a nonnegative Borel measurable function  on
on  and a nonnegative measure
and a nonnegative measure  on a Borel set
on a Borel set  . We define a capacity
. We define a capacity  by
by

where the supremum is taken over all nonnegative measures  such that
such that  (the support of
(the support of  ) is contained in
) is contained in  and
and  for every
for every  .
.
For  and
and  , we consider the function
, we consider the function  defined by
defined by

If  , then
, then  is extended to be continuous on
is extended to be continuous on  in the extended sense, where
in the extended sense, where  .
.
Now we will discuss the behavior at infinity of the modified Green potential and modified Poisson integral in the upper-half space, respectively. For related results, we refer the readers to the papers by Mizuta (see [9]), Siegel and Talvila (see [8]), and Mizuta and Shimomura (see [7]).
Theorem 1.1.
Let  be a positive nondecreasing function on the interval
be a positive nondecreasing function on the interval  such that
such that
(a) is nondecreasing on
is nondecreasing on  ,
,
(b) is nonincreasing on
is nonincreasing on  and
and  ,
,
(c)there exists a positive constant  such that
such that  for any
for any  .
.
Let  be a nonnegative measure on
be a nonnegative measure on  satisfying
satisfying

Then there exists a Borel set  with properties
with properties
(i)
(ii)
where  .
.
Corollary 1.2.
Let  be a nonnegative measure on
be a nonnegative measure on  satisfying
satisfying

Then there exists a Borel set  with properties
with properties
(i)
(ii)
where  .
.
Theorem 1.3.
Let  be defined as in Theorem 1.1 and
be defined as in Theorem 1.1 and  a nonnegative measure on
a nonnegative measure on  satisfying
satisfying

Then there exists a Borel set  with properties
with properties
(i)
(i)
where  .
.
Remark 1.4.
In the case  ,
,  .
.
Corollary 1.5.
Let  be a nonnegative measure on
be a nonnegative measure on  satisfying
satisfying

Then there exists a Borel set  satisfying Corollary 1.2 (ii) such that
satisfying Corollary 1.2 (ii) such that

We define the modified  -potentials on
-potentials on  by
by

where  and
and  (resp.,
(resp.,  ) is a nonnegative measure on
) is a nonnegative measure on  (resp.,
(resp.,  ) satisfying (1.18) (
) satisfying (1.18) ( ) (resp., (1.20)). Clearly,
) (resp., (1.20)). Clearly,  is a superharmonic function on
is a superharmonic function on  .
.
The following theorem follows readily from Theorems 1.1 and 1.3.
Theorem 1.6.
Let  be defined as in Theorem 1.1 and
be defined as in Theorem 1.1 and  defined by (1.23). Then there exists a Borel set
defined by (1.23). Then there exists a Borel set  satisfying Corollary 1.2 (ii) such that
satisfying Corollary 1.2 (ii) such that

Remark 1.7.
In the case  , by using Lemma 2.5 below, we can easily show that Corollary 1.2 (ii) with
, by using Lemma 2.5 below, we can easily show that Corollary 1.2 (ii) with  means that
means that  is
is  -rarefied at infinity in the sense of [12]. In particular, This condition with
-rarefied at infinity in the sense of [12]. In particular, This condition with  ,
,  , and
, and  (resp.,
(resp.,  ,
,  , and
, and  ) means that
) means that  is minimally thin at infinity (resp., rarefied at infinity) in the sense of [13].
is minimally thin at infinity (resp., rarefied at infinity) in the sense of [13].
Theorem 1.6 is the best possibility as to the size of the exceptional set. In fact we have the following result. The proof of it is essentially due to Mizuta (see [9, Theorem  ]), so we omit the proof here.
]), so we omit the proof here.
Theorem 1.8.
Let  be a Borel set satisfying Corollary 1.2 (ii),
be a Borel set satisfying Corollary 1.2 (ii),  defined as in Theorem 1.1, and
defined as in Theorem 1.1, and  defined by (1.23). Then we can find a nonnegative measure
defined by (1.23). Then we can find a nonnegative measure  defined on
defined on  satisfying
satisfying

such that

where  and
and  .
.
2. Some Lemmas
Throughout this paper, let  denote various constants independent of the variables in questions, which may be different from line to line.
denote various constants independent of the variables in questions, which may be different from line to line.
Lemma 2.1.
There exists a positive constant  such that
such that  where
where 
 , and
, and  in
in  .
.
This can be proved by simple calculation.
Lemma 2.2.
Gegenbauer polynomials have the following properties:
(i)
(ii)
(iii)
(iv) .
.
Proof.
-
(i)
and (ii) can be derived from [3]. (iii) follows by taking
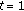 in (1.10); (iv) follows by (i), (ii) and the Mean Value Theorem for Derivatives.
in (1.10); (iv) follows by (i), (ii) and the Mean Value Theorem for Derivatives.
Lemma 2.3.
Let  be a nonnegative integer and
be a nonnegative integer and  ,
,  , then one has the following properties:
, then one has the following properties:
(i)
(ii)
(iii)
(iv) .
.
Lemma 2.4 (see [14]).
Let  be a nonnegative integer and
be a nonnegative integer and  .
.
(i)If  , then
, then  .
.
(ii)If  and
and  , then
, then  .
.
The following lemma can be proved by using Fuglede ([6, Théorèm  ]).
]).
Lemma 2.5.
For any Borel set  in
in  , we have
, we have  and
and

where the infimum is taken over all nonnegative measures  on
on  (resp.,
(resp.,  ) such that
) such that  for every
for every  .
.
3. Proof of Theorem 1.1
For any  , there exists
, there exists  such that
such that

For fixed  and
and  , we write
, we write

where

We distinguish the following two cases.
Case 1 ( ).
).
Note that  In view of (1.18), we can find a sequence
In view of (1.18), we can find a sequence  of positive numbers such that
of positive numbers such that  and
and  , where
, where

Consider the sets

for  If
If  is a nonnegative measure on
is a nonnegative measure on  such that
such that  and
and  for
for  , then we have
, then we have

So that

which yields

Setting  , we see that Theorem 1.1 (ii) is satisfied and
, we see that Theorem 1.1 (ii) is satisfied and

Moreover by Lemma 2.1,

Note that  . By (iii) and (iv) in Lemma 2.2, we take
. By (iii) and (iv) in Lemma 2.2, we take  ,
,  in Lemma 2.2 (iv) and obtain
in Lemma 2.2 (iv) and obtain

Similarly, we have by (iii) and (iv) in Lemma 2.2

By Lemma 2.1, we have

Similarly as  , we obtain
, we obtain

Finally, by Lemma 2.1, we have

Combining (3.9)–(3.15), we prove Case 1.
Case 2 ( ).
).
In this case, the growth estimates of  ,
,  ,
,  and
and  can be proved similarly as in Case 1. Inequations (3.9), (3.10), (3.13) and (3.15) still hold.
can be proved similarly as in Case 1. Inequations (3.9), (3.10), (3.13) and (3.15) still hold.
Moreover we have by Lemma 2.3 (iii)

By Lemma 2.3 (iv), we have

Similarly as  , we have
, we have

Combining (3.9), (3.10), (3.13), (3.15), and (3.16)–(3.18), we prove Case 2.
Hence we complete the proof of Theorem 1.1.
4. Proof of Theorem 1.3
For any  , there exists
, there exists  such that
such that

For fixed  and
and  , we write
, we write

where

First note that

Write

where

We obtain by Lemma 2.4 (i)

For  , by (4.7) we have
, by (4.7) we have

On the other hand, (4.7) yields that

Combining (4.8) and (4.9), we have

We have by Lemma 2.2 (iii)

By Lemma 2.4 (ii), we obtain

Note that  . By the lower semicontinuity of
. By the lower semicontinuity of  , we can prove the following fact in the same way as
, we can prove the following fact in the same way as  in the proof of Theorem 1.1:
in the proof of Theorem 1.1:

where 
 , and
, and  .
.
Combining (4.4) and (4.10)–(4.13), we complete the proof of Theorem 1.1.
References
Grafakos L: Classical and Modern Fourier Analysis. Pearson Education, Upper Saddle River, NJ, USA; 2004:xii+931.
Hörmander L: Notions of Convexity, Progress in Mathematics. Volume 127. Birkhäuser, Boston, Mass, USA; 1994:viii+414.
Szegő G: Orthogonal Polynomials. 4th edition. American Mathematical Society, Providence, RI, USA; 1975:xiii+432. American Mathematical Society, Colloquium Publications, Vol. XXII
Deng GT: Integral representations of harmonic functions in half spaces. Bulletin des Sciences Mathématiques 2007, 131(1):53–59.
Finkelstein M, Scheinberg S: Kernels for solving problems of Dirichlet type in a half-plane. Advances in Mathematics 1975, 18(1):108–113. 10.1016/0001-8708(75)90004-3
Fuglede B: Le théorème du minimax et la théorie fine du potentiel. Université de Grenoble. Annales de l'Institut Fourier 1965, 15(1):65–88. 10.5802/aif.196
Mizuta Y, Shimomura T: Growth properties for modified Poisson integrals in a half space. Pacific Journal of Mathematics 2003, 212(2):333–346. 10.2140/pjm.2003.212.333
Siegel D, Talvila E: Sharp growth estimates for modified Poisson integrals in a half space. Potential Analysis 2001, 15(4):333–360. 10.1023/A:1011817130061
Mizuta Y: On the behavior at infinity of Green potentials in a half space. Hiroshima Mathematical Journal 1980, 10(3):607–613.
Mizuta Y: Boundary limits of Green potentials of general order. Proceedings of the American Mathematical Society 1987, 101(1):131–135. 10.1090/S0002-9939-1987-0897083-5
Mizuta Y: On the boundary limits of Green potentials of functions. Journal of the Mathematical Society of Japan 1988, 40(4):583–594. 10.2969/jmsj/04040583
Aikawa H: On the behavior at infinity of nonnegative superharmonic functions in a half space. Hiroshima Mathematical Journal 1981, 11(2):425–441.
Essén M, Jackson HL: On the covering properties of certain exceptional sets in a half-space. Hiroshima Mathematical Journal 1980, 10(2):233–262.
Hayman WK, Kennedy PB: Subharmonic Functions. Academic Press, London, UK; 1976.
Acknowledgments
This work is supported by The National Natural Science Foundation of China under Grant 10671022 and Specialized Research Fund for the Doctoral Program of Higher Education under Grant 20060027023.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Qiao, L., Deng, G. Asymptotic Behavior for a Class of Modified  -Potentials in a Half Space.
J Inequal Appl 2010, 647627 (2010). https://doi.org/10.1155/2010/647627
-Potentials in a Half Space.
J Inequal Appl 2010, 647627 (2010). https://doi.org/10.1155/2010/647627
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/647627
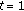 in (1.10); (iv) follows by (i), (ii) and the Mean Value Theorem for Derivatives.
in (1.10); (iv) follows by (i), (ii) and the Mean Value Theorem for Derivatives.