- Research Article
- Open access
- Published:
General Convexity of Some Functionals in Seminormed Spaces and Seminormed Algebras
Journal of Inequalities and Applications volume 2010, Article number: 643768 (2010)
Abstract
We prove some results for convex combination of nonnegative functionals, and some corollaries are established.
1. Introduction
Inequalities have been used in almost all the branches of mathematics. It is an important tool in the study of convex functions in seminormed space and seminormed algebras. Recently some works have been done by Altin et al. [1, 2], Tripathy et al. [1–6], Tripathy and Sarma [3, 4], Chandra and Tripathy [5], Tripathy and Mahanta [6], and many others involving inequalities in seminormed spaces and convex functions like the Orlicz function.
In this paper, inequalities for convex combinations of functionals satisfying conditions (a) and (b) are formulated in the theorems, and some corollaries are proved, using the theorems. Condition (a) relates to nonnegative functionals over which the inequalities in Theorems 1.1 and 1.4 on seminorm are proved. In Theorem 1.1, we consider seminormed spaces, and in Theorem 1.4 seminormed algebras. Condition (b) relates generally to the representations between seminormed spaces and seminormed algebras. The inequalities formulated in this way are proved in Corollaries 1.2 and 1.5. In this paper we consider the following generalization of the convexity in seminormed algebras.  , where
, where  ,
,  for
for  ,
,  is the norm in
is the norm in  , and
, and  is a real number.
is a real number.
In order to justify our study, we have provided an example related to real functions of one variable, similar examples can be constructed. This has been used in the geometry of Banach spaces as found in [7, 8]. Similar statements related to functionals in finite-dimensional spaces and countable dimensional spaces have been provided in [9]. These results can be applied in the mentioned areas.
Theorem 1.1.
Let  be a seminormed space over
be a seminormed space over  and the nonnegative functional f satisfy the following condition:
and the nonnegative functional f satisfy the following condition:
(a) , for all x,y with
, for all x,y with  , where
, where  are nondecreasing functions such that
are nondecreasing functions such that  . Then,
. Then,
(1)there exists  , where
, where

(2)the functions  and
and  are convex. Then, if
are convex. Then, if  ,
,  ,
,  ,
,  for
for  , the inequality
, the inequality  is satisfied.
is satisfied.
Proof.
Let  , as
, as  . We put
. We put  , where
, where  ,
,  ,
,  .
.
-
(a)
Let
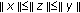 . According to condition (a), we obtain
. According to condition (a), we obtain 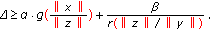 (1.2)
(1.2)
Knowing that  and
and  are nondecreasing, we obtain
are nondecreasing, we obtain

where  .
.
There exists  in compliance with (1). Therefore
in compliance with (1). Therefore  .
.
If we put  the result is
the result is  , that is,
, that is,  .
.
-
(b)
Let
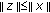 . Then, in view of (a), we have
. Then, in view of (a), we have  (1.4)
(1.4)
Let us consider  elements
elements  ,
, , and we suppose
, and we suppose  .
.
Let  , where
, where  , and
, and  ,
,  , as
, as  .
.
According to condition (a), we get

where  ,
,  .
.
Using the principle of induction over  , we will probe that
, we will probe that  .
.
We know that  , and therefore about
, and therefore about  the statement is proved. We assume the assertion about
the statement is proved. We assume the assertion about  is correct.
is correct.
-
(1)
Let
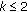 . Then,
. Then, 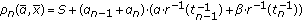 , where
, where 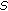 is the rest of the sum, and
is the rest of the sum, and 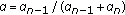 ,
, 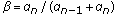 . With condition (2) we have
. With condition (2) we have 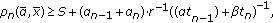 but
but 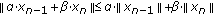 . Setting
. Setting  and knowing
and knowing  is nondecreasing function, we obtain
is nondecreasing function, we obtain 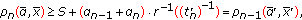 (1.6)
(1.6)
where  and
and  . With the inductive assumption,
. With the inductive assumption,  , that is,
, that is,  , that is,
, that is,  .
.
-
(2)
Let
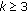 . Then
. Then  , where
, where 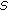 is the rest of the sum, and
is the rest of the sum, and 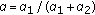 ,
, 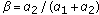 . According to condition (2), we obtain
. According to condition (2), we obtain 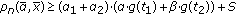 . Let us place
. Let us place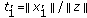 , where
, where 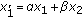 , but
, but 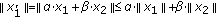 and
and 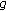 is a nondecreasing function. Then,
is a nondecreasing function. Then, 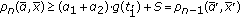 , where
, where 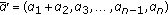 , and
, and 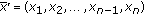 .
.
Applying the induction, we get  .
.
Corollary 1.2.
Let  and
and  be seminormed spaces over
be seminormed spaces over  and
and  . Then in Theorem 1.1, one replaces condition (a) by condition (b):
. Then in Theorem 1.1, one replaces condition (a) by condition (b):  , for all
, for all  with
with  , and all the rest of the conditions are satisfied. Then, with
, and all the rest of the conditions are satisfied. Then, with  ,
,  ,
,  ,
,  , the inequality
, the inequality  is satisfied.
is satisfied.
Proof.
We consider the functional  . Then, knowing (b), we conclude that
. Then, knowing (b), we conclude that  satisfies Theorem 1.1's conditions and hence the needed inequality.
satisfies Theorem 1.1's conditions and hence the needed inequality.
Example 1.3.
If we put in the conditions of Theorem 1.1,  ,
,  ,
,  ,
,  , and
, and  ,
,  ,
,  , then about
, then about  ,
, ,
,  ,
,  , we will obtain the inequality
, we will obtain the inequality

where

Proof.
Let us consider  , where
, where

Then,  ,
,

when  , that is,
, that is,  ; hence,
; hence,  . Further, we obtain
. Further, we obtain  . It is obvious that we have a minimum at this point in the interval
. It is obvious that we have a minimum at this point in the interval  .
.
Then, we obtain  , and hence at the same point
, and hence at the same point 

since

This confirms the assertion.
If we put  in the condition of the example, we receive
in the condition of the example, we receive  . Therefore,
. Therefore,  , when
, when  ,
,  ,
,  ,
,  .
.
Theorem 1.4.
Let  be a seminormed algebra over R with a unit. The functional
be a seminormed algebra over R with a unit. The functional  satisfies condition (a):
satisfies condition (a):  , for
, for  ,
,  as
as  , where
, where  are nondecreasing functions such that
are nondecreasing functions such that  .
.
Besides, the following requirements are fulfilled
(1)There exists  , where
, where

(2)The function,  and
and  are convex. Then, if
are convex. Then, if  ,
,  , one receives the inequality
, one receives the inequality

Proof.
Let  , as
, as  ,
,  .
.
We put  , where
, where  .
.
-
(a)
Let
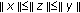 . According to condition (a), we have
. According to condition (a), we have 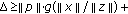
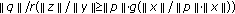 .
.
Here, we have  , and
, and  ,
,  are nondecreasing.
are nondecreasing.
If  ,
,  , then
, then  , where
, where  .
.
Then,  exist in compliance with (1). Therefore
exist in compliance with (1). Therefore  .
.
If we put  , the result is
, the result is  , that is,
, that is,  .
.
-
(b)
Let
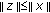 . Then, in view of the fact that (a), we get
. Then, in view of the fact that (a), we get  (1.15)
(1.15)
Let  ,
,  , as
, as  . Let us put
. Let us put  , where
, where  .
.
We can accept  . Let
. Let  and
and  .
.
We have  , where
, where

Applying the principle of induction over  we will prove that
we will prove that  . In view of the fact that was mentioned at the beginning, we get
. In view of the fact that was mentioned at the beginning, we get  . Assuming the statement for
. Assuming the statement for  holds, we will prove it for
holds, we will prove it for  .
.
-
(1)
Let
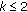 .
.
Putting  ,
,  , we have
, we have 
 where
where  is the rest of the sum. Using condition (2), we get
is the rest of the sum. Using condition (2), we get

Let  ,
,  .
.
Since  does not decrease, and
does not decrease, and  , then
, then 
 , where
, where  ,
,  , and
, and  .
.
By  we denote the unit of the algebra
we denote the unit of the algebra  . According to the inductive suggestion, we obtain
. According to the inductive suggestion, we obtain  .
.
-
(2)
Let
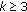 .
.
We set  ,
,  . As (2), we have
. As (2), we have 
 , where
, where  is the rest of the sum.
is the rest of the sum.
Let  ,
,  .
.
Since  does not decrease, and
does not decrease, and  , then
, then  , where
, where  ,
,  , and
, and  . According to the induction principle, we obtain
. According to the induction principle, we obtain  .
.
Corollary 1.5.
Let  be a seminormed algebra above
be a seminormed algebra above  with a unit, and let
with a unit, and let  be a seminormed space over
be a seminormed space over  , and
, and  .
.
Then, if one replaces the condition (a) in Theorem 1.4 by condition (c):  , for all
, for all  with
with  , and all the rest of the conditions are satisfied. One denotes by
, and all the rest of the conditions are satisfied. One denotes by  the norm in
the norm in  , and the norm in
, and the norm in  with
with  . Then if
. Then if  ,
,  one receives the inequality
one receives the inequality

Proof.
We consider the functional  . Then, knowing (c), we get that
. Then, knowing (c), we get that  satisfies Theorem 1.1's conditions and hence the needed inequality.
satisfies Theorem 1.1's conditions and hence the needed inequality.
References
Altin Y, Et M, Tripathy BC: The sequence space on seminormed spaces. Applied Mathematics and Computation 2004, 154(2):423–430. 10.1016/S0096-3003(03)00722-7
Tripathy BC, Altin Y, Et M: Generalized difference sequence spaces on seminormed space defined by Orlicz functions. Mathematica Slovaca 2008, 58(3):315–324. 10.2478/s12175-008-0077-0
Tripathy BC, Sarma B: Sequence spaces of fuzzy real numbers defined by Orlicz functions. Mathematica Slovaca 2008, 58(5):621–628. 10.2478/s12175-008-0097-9
Tripathy BC, Sarma B: Vector valued double sequence spaces defined by Orlicz function. Mathematica Slovaca 2009, 59(6):767–776. 10.2478/s12175-009-0162-z
Chandra P, Tripathy BC: On generalised Köthe-Toeplitz duals of some sequence spaces. Indian Journal of Pure and Applied Mathematics 2002, 33(8):1301–1306.
Tripathy BC, Mahanta S: On a class of generalized lacunary difference sequence spaces defined by Orlicz functions. Acta Mathematicae Applicatae Sinica 2004, 20(2):231–238. 10.1007/s10255-004-0163-1
Maleev RP, Troyanski SL: On the moduli of convexity and smoothness in Orlicz spaces. Studia Mathematica 1975, 54(2):131–141.
Maleev RP, Troyanski SL: On cotypes of Banach lattices. In Constructive Function Theory. Publishing House of the Slovak Academy of Sciences, Sofia, Bulgaria; 1983:429–441.
Stoyanov TS: Inequalities for convex combinations of functions. Proceedings of the 18th Spring-Conference of the Union of Bulgarian Mathematicians, April 1989, Albena, Bulgaria
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Stoyanov, T. General Convexity of Some Functionals in Seminormed Spaces and Seminormed Algebras. J Inequal Appl 2010, 643768 (2010). https://doi.org/10.1155/2010/643768
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/643768
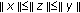 . According to condition (a), we obtain
. According to condition (a), we obtain 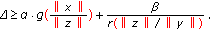
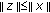 . Then, in view of (a), we have
. Then, in view of (a), we have 
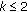 . Then,
. Then, 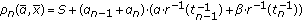 , where
, where 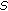 is the rest of the sum, and
is the rest of the sum, and 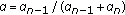 ,
, 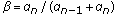 . With condition (2) we have
. With condition (2) we have 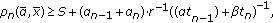 but
but 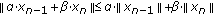 . Setting
. Setting  and knowing
and knowing  is nondecreasing function, we obtain
is nondecreasing function, we obtain 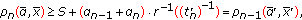
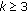 . Then
. Then  , where
, where 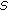 is the rest of the sum, and
is the rest of the sum, and 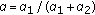 ,
, 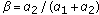 . According to condition (2), we obtain
. According to condition (2), we obtain 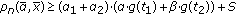 . Let us place
. Let us place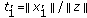 , where
, where 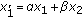 , but
, but 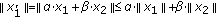 and
and 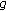 is a nondecreasing function. Then,
is a nondecreasing function. Then, 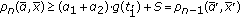 , where
, where 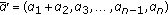 , and
, and 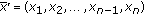 .
.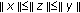 . According to condition (a), we have
. According to condition (a), we have 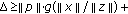
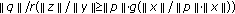 .
.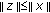 . Then, in view of the fact that (a), we get
. Then, in view of the fact that (a), we get 
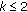 .
.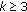 .
.