- Research Article
- Open access
- Published:
Multivariate Twisted 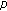 -Adic
-Adic 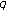 -Integral on
-Integral on  Associated with Twisted
Associated with Twisted 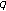 -Bernoulli Polynomials and Numbers
-Bernoulli Polynomials and Numbers
Journal of Inequalities and Applications volume 2010, Article number: 579509 (2010)
Abstract
Recently, many authors have studied twisted  -Bernoulli polynomials by using the
-Bernoulli polynomials by using the  -adic invariant
-adic invariant  -integral on
-integral on  . In this paper, we define the twisted
. In this paper, we define the twisted  -adic
-adic  -integral on
-integral on  and extend our result to the twisted
and extend our result to the twisted  -Bernoulli polynomials and numbers. Finally, we derive some various identities related to the twisted
-Bernoulli polynomials and numbers. Finally, we derive some various identities related to the twisted  -Bernoulli polynomials.
-Bernoulli polynomials.
1. Introduction
Let  be a fixed prime number. Throughout this paper, the symbols
be a fixed prime number. Throughout this paper, the symbols  and
and  will denote the ring of rational integers, the ring of
will denote the ring of rational integers, the ring of  -adic integers, the field of
-adic integers, the field of  -adic rational numbers, the complex number field, and the completion of the algebraic closure of
-adic rational numbers, the complex number field, and the completion of the algebraic closure of  respectively. Let
respectively. Let  be the set of natural numbers and
be the set of natural numbers and  Let
Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with 
When one talks of  -extension,
-extension,  is variously considered as an indeterminate, a complex
is variously considered as an indeterminate, a complex  or
or  -adic number
-adic number  If
If  one normally assumes that
one normally assumes that  If
If  then we assume that
then we assume that  .
.
For  let
let  be the
be the  -adic locally constant space defined by
-adic locally constant space defined by

where  is the cyclic group of order
is the cyclic group of order 
Let  be the space of uniformly differentiable function on
be the space of uniformly differentiable function on 
For  the
the  -adic invariant
-adic invariant  -integral on
-integral on  is defined as
is defined as

It is well known that the twisted  -Bernoulli polynomials of order
-Bernoulli polynomials of order  are defined as
are defined as

and  are called the twisted
are called the twisted  -Bernoulli numbers of order
-Bernoulli numbers of order  When
When  the polynomials and numbers are called the twisted
the polynomials and numbers are called the twisted  -Bernoulli polynomials and numbers, respectively. When
-Bernoulli polynomials and numbers, respectively. When  and
and  the polynomials and numbers are called the twisted Bernoulli polynomials and numbers, respectively. When
the polynomials and numbers are called the twisted Bernoulli polynomials and numbers, respectively. When  and
and  the polynomials and numbers are called the ordinary Bernoulli polynomials and numbers, respectively.
the polynomials and numbers are called the ordinary Bernoulli polynomials and numbers, respectively.
Many authors have studied the twisted  -Bernoulli polynomials by using the properties of the
-Bernoulli polynomials by using the properties of the  -adic invariant
-adic invariant  -integral on
-integral on  (cf. [4]). In this paper, we define the twisted
(cf. [4]). In this paper, we define the twisted  -adic
-adic  -integral on
-integral on  and extend our result to the twisted
and extend our result to the twisted  -Bernoulli polynomials and numbers. Finally, we derive some various identities related to the twisted
-Bernoulli polynomials and numbers. Finally, we derive some various identities related to the twisted  -Bernoulli polynomials.
-Bernoulli polynomials.
2. Multivariate Twisted 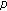 -Adic
-Adic 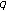 -Integral on
-Integral on  Associated withTwisted
Associated withTwisted  -Bernoulli Polynomials
-Bernoulli Polynomials
In this section, we assume that  with
with  For
For  , we define the
, we define the  -numbers as
-numbers as

Note that  .
.
Let us define

where  Note that
Note that 
Now we construct the twisted  -adic
-adic  -integral on
-integral on  as follows:
as follows:

where  From the definition of the twisted
From the definition of the twisted  -adic
-adic  -integral on
-integral on  , we can consider the twisted
, we can consider the twisted  -Bernoulli polynomials and numbers of order
-Bernoulli polynomials and numbers of order  as follows:
as follows:

In the special case  in (2.4),
in (2.4),  are called the twisted
are called the twisted  -Bernoulli numbers of order
-Bernoulli numbers of order  .
.
If we take  and
and  in (2.4), we can easily see that
in (2.4), we can easily see that

compare with [4].
Theorem 2.1.
For  and
and  we have
we have

Moreover, if we take  in Theorem 2.1, then we have the following identity for the twisted
in Theorem 2.1, then we have the following identity for the twisted  -Bernoull numbers
-Bernoull numbers

From the definition of multivariate twisted  -adic
-adic  -integral, we also see that
-integral, we also see that

Corollary 2.2.
For  and
and  , one obtains
, one obtains

Note that

We have

It is easy to see that

By (2.11) and (2.12), we obtain the following theorem.
Theorem 2.3.
For  and
and  one has
one has

Now we consider the modified extension of the twisted  -Bernoulli polynomials of order
-Bernoulli polynomials of order  as follows:
as follows:

In the special case  we write
we write  which are called the modified extension of the twisted
which are called the modified extension of the twisted  -Bernoulli numbers of order
-Bernoulli numbers of order 
From (2.14), we derive that

Therefore, we obtain the following theorem.
Theorem 2.4.
For  and
and  one has
one has

Now, we define  as follows:
as follows:

By (2.17), we can see that

Therefore, we obtain the following theorem.
Theorem 2.5.
For  and
and  one has
one has

In (2.19), we can see the relations between the binomial coefficients and the modified extension of the twisted  -Bernoulli polynomials of order
-Bernoulli polynomials of order 
References
Jang L-C: Multiple twisted -Euler numbers and polynomials associated with -adic -integrals. Advances in Difference Equations 2008, -11.
Kim T: -Volkenborn integration. Russian Journal of Mathematical Physics 2002, 9(3):288–299.
Kim T: -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008, 15(1):51–57.
Kim T: Sums of products of -Bernoulli numbers. Archiv der Mathematik 2001, 76(3):190–195. 10.1007/s000130050559
Acknowledgments
The authors would like to thank the anonymous referee for his/her excellent detail comments and suggestions. This Research was supported by Kyungpook National University Research Fund, 2010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rim, SH., Moon, EJ., Lee, SJ. et al. Multivariate Twisted 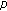 -Adic
-Adic 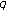 -Integral on
-Integral on  Associated with Twisted
Associated with Twisted 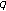 -Bernoulli Polynomials and Numbers.
J Inequal Appl 2010, 579509 (2010). https://doi.org/10.1155/2010/579509
-Bernoulli Polynomials and Numbers.
J Inequal Appl 2010, 579509 (2010). https://doi.org/10.1155/2010/579509
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/579509
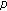 -Adic
-Adic 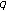 -Integral on
-Integral on  Associated withTwisted
Associated withTwisted  -Bernoulli Polynomials
-Bernoulli Polynomials