- Research Article
- Open access
- Published:
Nonlinear Boundary Value Problem of First-Order Impulsive Functional Differential Equations
Journal of Inequalities and Applications volume 2010, Article number: 490741 (2010)
Abstract
This paper investigates the nonlinear boundary value problem for a class of first-order impulsive functional differential equations. By establishing a comparison result and utilizing the method of upper and lower solutions, some criteria on the existence of extremal solutions as well as the unique solution are obtained. Examples are discussed to illustrate the validity of the obtained results.
1. Introduction
It is now realized that the theory of impulsive differential equations provides a general framework for mathematical modelling of many real world phenomena. In particular, it serves as an adequate mathematical tool for studying evolution processes that are subjected to abrupt changes in their states. Some typical physical systems that exhibit impulsive behaviour include the action of a pendulum clock, mechanical systems subject to impacts, the maintenance of a species through periodic stocking or harvesting, the thrust impulse maneuver of a spacecraft, and the function of the heart. For an introduction to the theory of impulsive differential equations, refer to [1].
It is also known that the method of upper and lower solutions coupled with the monotone iterative technique is a powerful tool for obtaining existence results of nonlinear differential equations [2]. There are numerous papers devoted to the applications of this method to nonlinear differential equations in the literature, see [3–9] and references therein. The existence of extremal solutions of impulsive differential equations is considered in papers [3–11]. However, only a few papers have implemented the technique in nonlinear boundary value problem of impulsive differential equations [5, 12]. In this paper, we will investigate nonlinear boundary value problem of a class of first-order impulsive functional differential equations. Such equations include the retarded impulsive differential equations as special cases [5, 12–14].
The rest of this paper is organized as follows. In Section 2, we establish a new comparison principle and discuss the existence and uniqueness of the solution for first order impulsive functional differential equations with linear boundary condition. We then obtain existence results for extremal solutions and unique solution in Section 3 by using the method of upper and lower solutions coupled with monotone iterative technique. To illustrate the obtained results, two examples are discussed in Section 4.
2. Preliminaries
Let  ,
,  ,
,  with
with  . We define that
. We define that  is continuous for any
is continuous for any  ;
;  and
and  exist and
exist and  ,
,  is continuously differentiable for any
is continuously differentiable for any  ;
;  ,
,  exist and
exist and  . It is clear that
. It is clear that  and
and  are Banach spaces with respective norms
are Banach spaces with respective norms

Let us consider the following nonlinear boundary value problem (NBVP):

where  is continuous in the second and the third variables, and for fixed
is continuous in the second and the third variables, and for fixed  ,
,  ,
,  ,
,  ,
,  and
and  is continuous.
is continuous.
A function  is called a solutions of NBVP (2.2) if it satisfies (2.2).
is called a solutions of NBVP (2.2) if it satisfies (2.2).
Remark 2.1.
-
(i)
If
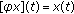 and the impulses
and the impulses 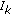 depend only on
depend only on 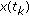 , the equation of NBVP (2.2) reduces to the simpler case of impulsive differential equations:
, the equation of NBVP (2.2) reduces to the simpler case of impulsive differential equations: 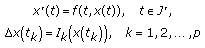 (2.3)
(2.3)
which have been studied in many papers. In some situation, the impulse  depends also on some other parameters (e.g., the control of the amount of drug ingested by a patient at certain moments in the model for drug distribution [1, 3]).
depends also on some other parameters (e.g., the control of the amount of drug ingested by a patient at certain moments in the model for drug distribution [1, 3]).
-
(ii)
If
 , where
, where 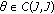 , the equation of NBVP (2.2) can be regarded as retarded differential equation which has been considered in [5, 12–14].
, the equation of NBVP (2.2) can be regarded as retarded differential equation which has been considered in [5, 12–14].
We will need the following lemma.
Lemma 2.2 (see [1]).
Asumme that
the sequence  satisfies
satisfies  with
with  ,
,
 is left continous at
is left continous at  for
for  ,
,
for  ,
, ,
,

where  ,
,  and
and  are real constants.
are real constants.
Then

In order to establish a comparison result and some lemmas, we will make the following assumptions on the function  .
.
(H1) There exists a constant  such that
such that

(H2) The function  satisfies Lipschitz condition, that is, there exists a
satisfies Lipschitz condition, that is, there exists a  such that
such that

Inspired by the ideas in [5, 6], we shall establish the following comparison result.
Theorem 2.3.
Let  such that
such that

where  ,
,  ,
,  ,
,  , and
, and  .
.
Suppose in addition that condition (H1) holds and

then  .
.
Proof.
For simplicity, we let  ,
,  . Set
. Set  , then we have
, then we have

Obviously,  implies
implies  .
.
To show  , we suppose, on the contrary, that
, we suppose, on the contrary, that  for some
for some  . It is enough to consider the following cases.
. It is enough to consider the following cases.
(i)there exists a  , such that
, such that  , and
, and  for all
for all  ;
;
(ii)there exist  , such that
, such that  ,
,  .
.
Casedi.
By (2.10), we have  for
for  and
and  ,
,  , hence
, hence  is nonincreasing in
is nonincreasing in  , that is,
, that is,  . If
. If  , then
, then  , which is a contradiction. If
, which is a contradiction. If  , then
, then  which implies
which implies  . But from (2.10), we get
. But from (2.10), we get  for
for  . Hence,
. Hence,  . It is again a contradiction.
. It is again a contradiction.
Casedii.
Let  , then
, then  . For some
. For some  , there exists
, there exists  such that
such that  or
or  . We only consider
. We only consider  , as for the case
, as for the case  , the proof is similar.
, the proof is similar.
From (2.10) and condition (H1), we get

Consider the inequalities

By Lemma 2.2, we have

that is

First, we assume that  . Let
. Let  in (2.14), then
in (2.14), then

Noting that  , we have
, we have

Hence

which is a contradiction.
Next, we assume that  . By Lemma 2.2 and (2.10), we have
. By Lemma 2.2 and (2.10), we have

then

Setting  in (2.14), we have
in (2.14), we have

with (2.19), we obtain that

that is,

Therefore,

which is a contradiction. The proof of Theorem 2.3 is complete.
The following corollary is an easy consequence of Theorem 2.3.
Corollary 2.4.
Assume that there exist  ,
,  ,
,  , for
, for  such that
such that  satisfies (2.8) with
satisfies (2.8) with  and
and

then  , for
, for  .
.
Remark 2.5.
Setting  , Corollary 2.4 reduces to the Theorem 2.3 of Li and Shen [6]. Therefore, Theorem 2.3 and Corollary 2.4 develops and generalizes the result in [6].
, Corollary 2.4 reduces to the Theorem 2.3 of Li and Shen [6]. Therefore, Theorem 2.3 and Corollary 2.4 develops and generalizes the result in [6].
Remark 2.6.
We show some examples of function  satisfying (H1).
satisfying (H1).
(i) , where
, where  , satisfies (H1) with
, satisfies (H1) with  ,
,

(ii) , satisfies (H1) with
, satisfies (H1) with  ,
,

Consider the linear boundary value problem (LBVP)

where  ,
,  ,
,  ,
,  , and
, and  .
.
By direct computation, we have the following result.
Lemma 2.7.

is a solution of LBVP (2.27) if and only if  is a solution of the impulsive integral equation
is a solution of the impulsive integral equation

where  ,
,  ,
,  and
and

Lemma 2.8.
Let (H2) hold. Suppose further

where  ,
,  ,
,  , then LBVP (2.27) has a unique solution.
, then LBVP (2.27) has a unique solution.
By Lemma 2.7 and Banach fixed point theorem, the proof of Lemma 2.8 is apparent, so we omit the details.
3. Main Results
In this section, we use monotone iterative technique to obtain the existence results of extremal solutions and the unique solution of NBVP (2.2). We shall need the following definition.
Definition 3.1.
A function  is said to be a lower solution of NBVP (2.2) if it satisfies
is said to be a lower solution of NBVP (2.2) if it satisfies

Analogously,  is an upper solution of NBVP (2.2) if
is an upper solution of NBVP (2.2) if

For convenience, let us list the following conditions.
(H3) There exist constants  ,
,  such that
such that

wherever  .
.
(H4) There exist constants  for
for  such that
such that

wherever  .
.
(H5) The function  satisfies
satisfies

(H6) There exist constants  ,
,  with
with  such that
such that

wherever  , and
, and  .
.
Let  . Now we are in the position to establish the main results of this paper.
. Now we are in the position to establish the main results of this paper.
Theorem 3.2.
Let ( )–(
)–( ) and inequalities (2.9) and (2.30) hold. Assume further that there exist lower and upper solutions
) and inequalities (2.9) and (2.30) hold. Assume further that there exist lower and upper solutions  and
and  of NBVP (2.2), respectively, such that
of NBVP (2.2), respectively, such that  on
on  . Then there exist monotone sequences
. Then there exist monotone sequences  with
with  , such that
, such that  ,
,  uniformly on
uniformly on  . Moreover,
. Moreover,  ,
,  are minimal and maximal solutions of NBVP (2.2) in
are minimal and maximal solutions of NBVP (2.2) in  , respectively.
, respectively.
Proof.
For any  , consider LVBP (2.27) with
, consider LVBP (2.27) with

By Lemma 2.8, we know that LBVP (2.27) has a unique solution  . Define an operator
. Define an operator  by
by  , then the operator
, then the operator  has the following properties:
has the following properties:
(a) ,
, 
(b) , if
, if 
To prove (a), let  and
and  .
.

By Theorem 2.3, we get  for
for  , that is,
, that is,  . Similarly, we can show that
. Similarly, we can show that  .
.
To prove (b), set  , where
, where  and
and  . Using (H3), (H4) and (H6), we get
. Using (H3), (H4) and (H6), we get

By Theorem 2.3, we get  for
for  , that is,
, that is,  , then (b) is proved.
, then (b) is proved.
Let  and
and  for
for  By the properties (a) and (b), we have
By the properties (a) and (b), we have

By the definition of operator  , we have that
, we have that  and
and  are uniformly bounded in
are uniformly bounded in  . Thus
. Thus  and
and  are uniformly bounded and equicontinuous in
are uniformly bounded and equicontinuous in  . By Arzela-Ascoli Theorem and (3.10), we know that there exist
. By Arzela-Ascoli Theorem and (3.10), we know that there exist  ,
,  in
in  such that
such that

Moreover,  ,
,  are solutions of NBVP (2.2) in
are solutions of NBVP (2.2) in  .
.
To prove that  ,
,  are extremal solutions of NBVP (2.2), let
are extremal solutions of NBVP (2.2), let  be any solution of NBVP (2.2), that is,
be any solution of NBVP (2.2), that is,

By Theorem 2.3 and Induction, we get  with
with  and
and  which implies that
which implies that  , that is,
, that is,  and
and  are minimal and maximal solution of NBVP (2.2) in
are minimal and maximal solution of NBVP (2.2) in  , respectively. The proof is complete.
, respectively. The proof is complete.
Theorem 3.3.
Let the assumptions of Theorem 3.2 hold and assume the following.
(H7) There exist constants  ,
,  such that
such that

where  .
.
(H8) There exist constants  ,
,  such that
such that

where  .
.
(H9) There exist constants  ,
,  with
with  such that
such that

whenever  , and
, and  .
.
Then NBVP (2.2) has a unique solution in  .
.
Proof.
By Theorem 3.2, we know that there exist  , which are minimal and maximal solutions of NBVP (2.2) with
, which are minimal and maximal solutions of NBVP (2.2) with  .
.
Let  . Using (H7), (H8), and (H9), we get
. Using (H7), (H8), and (H9), we get

By Theorem 2.3, we have that  ,
,  , that is,
, that is,  . Hence
. Hence  , this completes the proof.
, this completes the proof.
4. Examples
To illustrate our main results, we shall discuss in this section some examples.
Example 4.1.
Consider the problem

where  ,
,  ,
,  .
.
Let

Setting  and
and  , it is easy to verify that
, it is easy to verify that  is a lower solution, and
is a lower solution, and  is an upper solution with
is an upper solution with  .
.
For  , and
, and  , we have
, we have

Setting  ,
,  ,
,  ,
,  ,
,  and
and  ,
,  , then conditions (H1)–(H6) are all satisfied:
, then conditions (H1)–(H6) are all satisfied:

then inequalities (2.9) and (2.30) are satisfied. By Theorem 3.2, problem (4.1) has extremal solutions  .
.
Example 4.2.
Consider the problem

where  ,
,  ,
,  .
.
Let

Setting  and
and  , then
, then  is a lower solution, and
is a lower solution, and  is an upper solution with
is an upper solution with  .
.
For  , and
, and  , we have
, we have  ,
,  , and
, and  . Setting
. Setting  ,
,  ,
,  ,
,  ,
,  and
and  ,
,  , then conditions (H1)–(H6) are all satisfied:
, then conditions (H1)–(H6) are all satisfied:

then inequalities (2.24) and (2.30) are satisfied. By Corollary 2.4 and Theorem 3.2, problem (4.5) has extremal solutions  .
.
Moreover, let  ,
,  ,
,  and
and  ,
,  . It is easy to see that conditions (H7)–(H9) are satisfied. By Corollary 2.4 and Theorem 3.3, problem (4.5) has an unique solution in
. It is easy to see that conditions (H7)–(H9) are satisfied. By Corollary 2.4 and Theorem 3.3, problem (4.5) has an unique solution in  .
.
References
Lakshmikanthan V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations. World Scientific, Singapore; 1989.
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Franco D, Liz E, Nieto JJ, Rogovchenko YV: A contribution to the study of functional differential equations with impulses. Mathematische Nachrichten 2000, 218: 49–60. 10.1002/1522-2616(200010)218:1<49::AID-MANA49>3.0.CO;2-6
Nieto JJ, Rodríguez-López R: Boundary value problems for a class of impulsive functional equations. Computers & Mathematics with Applications 2008, 55(12):2715–2731. 10.1016/j.camwa.2007.10.019
Chen L, Sun J: Nonlinear boundary value problem of first order impulsive functional differential equations. Journal of Mathematical Analysis and Applications 2006, 318(2):726–741. 10.1016/j.jmaa.2005.08.012
Li L, Shen J: Periodic boundary value problems for functional differential equations with impulses. Mathematica Scientia 2005, 25A: 237–244.
Liu X, Guo D: Periodic boundary value problems for a class of second-order impulsive integro-differential equations in Banach spaces. Journal of Mathematical Analysis and Applications 1997, 216(1):284–302. 10.1006/jmaa.1997.5688
Guo D, Liu X: Periodic boundary value problems for impulsive integro-differential equations in Banach spaces. Nonlinear World 1996, 3(3):427–441.
Liu X, Guo D: Initial value problems for first order impulsive integro-differential equations in Banach spaces. Communications on Applied Nonlinear Analysis 1995, 2(1):65–83.
Guo D, Liu X: First order impulsive integro-differential equations on unbounded domain in a Banach space. Dynamics of Continuous, Discrete and Impulsive Systems 1996, 2(3):381–394.
Franco D, Nieto JJ: First-order impulsive ordinary differential equations with anti-periodic and nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2000, 42(2):163–173. 10.1016/S0362-546X(98)00337-X
Yang X, Shen J: Nonlinear boundary value problems for first order impulsive functional differential equations. Applied Mathematics and Computation 2007, 189(2):1943–1952. 10.1016/j.amc.2006.12.085
Ding W, Mi J, Han M: Periodic boundary value problems for the first order impulsive functional differential equations. Applied Mathematics and Computation 2005, 165(2):433–446. 10.1016/j.amc.2004.06.022
Luo Z, Jing Z: Periodic boundary value problem for first-order impulsive functional differential equations. Computers & Mathematics with Applications 2008, 55(9):2094–2107.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, K., Liu, X. Nonlinear Boundary Value Problem of First-Order Impulsive Functional Differential Equations. J Inequal Appl 2010, 490741 (2010). https://doi.org/10.1155/2010/490741
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/490741
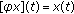 and the impulses
and the impulses 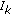 depend only on
depend only on 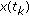 , the equation of NBVP (2.2) reduces to the simpler case of impulsive differential equations:
, the equation of NBVP (2.2) reduces to the simpler case of impulsive differential equations: 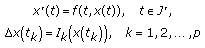
 , where
, where 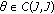 , the equation of NBVP (2.2) can be regarded as retarded differential equation which has been considered in [
, the equation of NBVP (2.2) can be regarded as retarded differential equation which has been considered in [