- Research Article
- Open access
- Published:
A Shrinking Projection Method for Generalized Mixed Equilibrium Problems, Variational Inclusion Problems and a Finite Family of Quasi-Nonexpansive Mappings
Journal of Inequalities and Applications volume 2010, Article number: 458247 (2010)
Abstract
The purpose of this paper is to consider a shrinking projection method for finding a common element of the set of solutions of generalized mixed equilibrium problems, the set of fixed points of a finite family of quasi-nonexpansive mappings, and the set of solutions of variational inclusion problems. Then, we prove a strong convergence theorem of the iterative sequence generated by the shrinking projection method under some suitable conditions in a real Hilbert space. Our results improve and extend recent results announced by Peng et al. (2008), Takahashi et al. (2008), S.Takahashi and W. Takahashi (2008), and many others.
1. Introduction
Throughout this paper, we assume that  is a real Hilbert space with inner product
is a real Hilbert space with inner product  and norm
and norm  , and let
, and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . We denote weak convergence and strong convergence by notations
. We denote weak convergence and strong convergence by notations  and
and  , respectively.
, respectively.
Recall that the following definitions.
(1)A mapping  is said to be nonexpansive if
is said to be nonexpansive if

(2)A mapping  is said to be quasi-nonexpansive if
is said to be quasi-nonexpansive if

We denote  be the set of fixed points of
be the set of fixed points of  .
.
Let  be a single-valued nonlinear mapping and
be a single-valued nonlinear mapping and  to a set-valued mapping. The variational inclusion problem is to find
to a set-valued mapping. The variational inclusion problem is to find  such that
such that

where  is the zero vector in
is the zero vector in  . The set of solutions of problem (1.3) is denoted by
. The set of solutions of problem (1.3) is denoted by  .
.
Definition 1.1.
A mapping  is said to be a
is said to be a  -inverse-strongly monotone if there exists a constant
-inverse-strongly monotone if there exists a constant  with the property
with the property

Remark 1.2.
It is obvious that any  -inverse-strongly monotone mapping
-inverse-strongly monotone mapping  is monotone and
is monotone and  -Lipschitz continuous. It is easy to see that if any
-Lipschitz continuous. It is easy to see that if any  constant is in
constant is in  , then the mapping
, then the mapping  is nonexpansive, where
is nonexpansive, where  is the identity mapping on
is the identity mapping on 
A set-valued mapping  is called monotone if for all
is called monotone if for all  , and
, and  implying
implying  . A monotone mapping;
. A monotone mapping;  is maximal if its graph
is maximal if its graph  of
of  is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping  is maximal if and only if for
is maximal if and only if for  for all
for all  imply
imply  .
.
Definition 1.3.
Let  be a set-valued maximal monotone mapping, then the single-valued mapping
be a set-valued maximal monotone mapping, then the single-valued mapping  defined by
defined by

is called the resolvent operator associated with  , where
, where  is any positive number and
is any positive number and  is the identity mapping.
is the identity mapping.
Remark 1.4.
(R1) The resolvent operator  is single-valued and nonexpansive for all
is single-valued and nonexpansive for all  , that is,
, that is,

(R2)The resolvent operator  is 1-inverse strongly monotone; see [1], that is,
is 1-inverse strongly monotone; see [1], that is,

(R3)The solution of problem (1.3) is a fixed point of the operator  for all
for all  ; see also [2], that is,
; see also [2], that is,

(R4)If  , then the mapping
, then the mapping  is nonexpansive.
is nonexpansive.
(R5) is closed and convex.
is closed and convex.
Let  be a nonlinear mapping, let
be a nonlinear mapping, let  be a real-valued function and
be a real-valued function and  a bifunction from
a bifunction from  to
to  . We consider the following generalized mixed equilibrium problem.
. We consider the following generalized mixed equilibrium problem.
Finding  such that
such that

The set of such  is denoted by
is denoted by  that is,
that is,

It is easy to see that  is solution of problem (1.9) implies that
is solution of problem (1.9) implies that  .
.
(i)In the case of  (:the zero mapping), then the generalized mixed equilibrium problem (1.9) is reduced to the mixed equilibrium problem. Finding
(:the zero mapping), then the generalized mixed equilibrium problem (1.9) is reduced to the mixed equilibrium problem. Finding  such that
such that

The set of solution of (1.11) isdenoted by 
(ii)In the case of  , then the generalized mixed equilibrium problem (1.9) is reduced to the generalized equilibrium problem. Finding
, then the generalized mixed equilibrium problem (1.9) is reduced to the generalized equilibrium problem. Finding  such that
such that

The set of solution of (1.12) is denoted by 
(iii)In the case of  (:the zero mapping) and
(:the zero mapping) and  , then the generalized mixed equilibrium problem (1.9) is reduced to the equilibrium problem. Finding
, then the generalized mixed equilibrium problem (1.9) is reduced to the equilibrium problem. Finding  such that
such that

The set of solution of (1.13) is denoted by 
(iv)In the case of  ,
,  and
and  then the generalized mixed equilibrium problem (1.9) is reduced to the variational inequality problem. Finding
then the generalized mixed equilibrium problem (1.9) is reduced to the variational inequality problem. Finding  such that
such that

The set of solution of (1.14) is denoted by 
The generalized mixed equilibrium problem include fixed point problems, optimization problems, variational inequalities problems, Nash equilibrium problems, noncooperative games, economics and the equilibrium problems as special cases (see, e.g., [3–8]). Some methods have been proposed to solve the generalized mixed equilibrium problems, generalized equilibrium problems and equilibrium problems; see, for instance, [9–22].
In 2007, Takahashi et al. [23] proved the following strong convergence theorem for a nonexpansive mapping by using the shrinking projection method in mathematical programming. For a  and
and  , they defined a sequence as follows
, they defined a sequence as follows

where  . They proved that the sequence
. They proved that the sequence  generated by (1.15) converges weakly to
generated by (1.15) converges weakly to  , where
, where 
In 2008, S. Takahashi and W. Takahashi [24] introduced the following iterative scheme for finding a common element of the set of solutions of mixed equilibrium problems and the set of fixed points of a nonexpansive mapping in a Hilbert space. Starting with arbitrary  , define sequences
, define sequences  ,
,  and
and  by
by

They proved that under certain appropriate conditions imposed on  ,
, and
and  , the sequence
, the sequence  generated by (1.16) converges strongly to
generated by (1.16) converges strongly to 
In 2008, Zhang et al. [25] introduced the following new iterative scheme for finding a common element of the set of solutions to the problem (1.3) and the set of fixed points of a nonexpansive mapping in a real Hilbert space. Starting with an arbitrary  , define sequences
, define sequences  and
and  by
by

where  is the resolvent operator associated with
is the resolvent operator associated with  and a positive number
and a positive number  is a sequence in the interval
is a sequence in the interval  .
.
In 2008, Peng et al. [26] introduced the following iterative scheme by the viscosity approximation method for finding a common element of the set of solutions to the problem (1.3), the set of solutions of an equilibrium problems and the set of fixed points of nonexpansive mappings in a Hilbert space. Starting with an arbitrary  , define sequences
, define sequences  and
and  by
by

They proved that under certain appropriate conditions imposed on  and
and  , the sequence
, the sequence  generated by (1.18) converges strongly to
generated by (1.18) converges strongly to 
In 2010, Katchang and Kumam [27] introduced an iterative scheme for finding a common element of the set of solutions for mixed equilibrium problems, the set of solutions of the variational inclusions with set-valued maximal monotone mappings, and inverse strongly monotone mappings and the set of fixed points of a finite family of nonexpansive mappings in a real Hilbert space.
In this paper, motivated and inspired by the previously mentioned results, we introduce an iterative scheme by the shrinking projection method for finding a common element of the set of solutions of generalized mixed equilibrium problems, the set of fixed points of a finite family of quasi-nonexpansive mappings and the set of solutions of variational inclusion problems in a real Hilbert space. Then, we prove a strong convergence theorem of the iterative sequence generated by the proposed shrinking projection method under some suitable conditions. The results obtained in this paper extend and improve several recent results in this area.
2. Preliminaries
Let  be a real Hilbert space and let
be a real Hilbert space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Recall that the (nearest point) projection
Recall that the (nearest point) projection  from
from  onto
onto  assigns to each
assigns to each  the unique point in
the unique point in  satisfying the property
satisfying the property

We recall some lemmas which will be needed in the rest of this paper.
Lemma 2.1.
For a given  and
and  ,
,

It is well known that  is a firmly nonexpansive mapping of
is a firmly nonexpansive mapping of  onto
onto  and satisfies
and satisfies

Lemma 2.2 (see [1]).
Let  be a maximal monotone mapping and let
be a maximal monotone mapping and let  be a Lipshitz continuous mapping. Then the mapping
be a Lipshitz continuous mapping. Then the mapping  is a maximal monotone mapping.
is a maximal monotone mapping.
Lemma 2.3 (see [28]).
Let  be a closed convex subset of
be a closed convex subset of  and let
and let  be a bounded sequence in
be a bounded sequence in  . Assume that
. Assume that
(1)the weak  -limit set
-limit set  ,
,
(2)for each  ,
,  exists.
exists.
Then  is weakly convergent to a point in
is weakly convergent to a point in  .
.
Lemma 2.4 (see [29]).
Each Hilbert space  satisfies Opial's condition, that is, for any sequence
satisfies Opial's condition, that is, for any sequence  with
with  , the inequality
, the inequality

holds for each  with
with  .
.
Lemma 2.5 (see [30]).
Each Hilbert space  satisfies the Kadec-Klee property, that is, for any sequence
satisfies the Kadec-Klee property, that is, for any sequence  with
with  and
and  together imply
together imply  .
.
For solving the generalized equilibrium problems, let us give the following assumptions for  and the set
and the set  :
:
(A1) for all
for all 
(A2) is monotone, that is,
is monotone, that is,  for all
for all 
(A3)for each  is weakly upper semicontinuous;
is weakly upper semicontinuous;
(A4)for each  is convex and lower semicontinuous;
is convex and lower semicontinuous;
(B1)for each  and
and  there exists a bounded subset
there exists a bounded subset  and
and  such that for any
such that for any 

(B2)C is bounded set.
Lemma 2.6 (see [31]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a bifunction of
be a bifunction of  into
into  satisfying (A1)–(A4). Let
satisfying (A1)–(A4). Let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . For
. For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

Assume that either  or
or  holds. Then, the following conclusions hold:
holds. Then, the following conclusions hold:
(1)for each 
(2) is single-valued;
is single-valued;
(3) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any 

(4)
(5) is closed and convex.
is closed and convex.
Remark 2.7.
Replacing  with
with  in (2.5), then there exists
in (2.5), then there exists  , such that
, such that

3. Main Results
In this section, we will introduce an iterative scheme by using shrinking projection method for finding a common element of the set of solutions of generalized mixed equilibrium problems, the set of fixed points of a finite family of quasi-nonexpansive mappings and the set of solutions of variational inclusion problems in a real Hilbert space.
Let  be a finite family of nonexpansive mappings of
be a finite family of nonexpansive mappings of  into itself, and let
into itself, and let  be real numbers such that
be real numbers such that  for every
for every  . We define a mapping
. We define a mapping  as follows:
as follows:

Such a mapping  is called the K-mapping generated by
is called the K-mapping generated by  and
and  ; see [32].
; see [32].
We have the following crucial Lemma 3.1 and Lemma 3.2 concerning  -mapping which can be found in [14]. Now we only need the following similar version in Hilbert spaces.
-mapping which can be found in [14]. Now we only need the following similar version in Hilbert spaces.
Lemma 3.1.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a finite family of quasi-nonexpansive mappings and
be a finite family of quasi-nonexpansive mappings and  -Lipschitz mappings of
-Lipschitz mappings of  into itself with
into itself with  and let
and let  be real numbers such that
be real numbers such that  for every
for every  ,
,  and
and  . Let
. Let  be the K-mapping generated by
be the K-mapping generated by  and
and  . Then, the followings hold:
. Then, the followings hold:
(1) is quasi-nonexpansive and Lipschitz,
is quasi-nonexpansive and Lipschitz,
(2) .
.
Lemma 3.2.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a finite family of quasi-nonexpansive mappings and
be a finite family of quasi-nonexpansive mappings and  -Lipschitz mappings of
-Lipschitz mappings of  into itself and
into itself and  sequences in
sequences in  such that
such that  Moreover, for every
Moreover, for every  , let
, let  and
and  be the K-mappings generated by
be the K-mappings generated by  and
and  , and
, and  and
and  , respectively. Then, for every
, respectively. Then, for every  , we have
, we have 
Now we study the strong convergence theorem concerning the shrinking projection method.
Theorem 3.3.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), and let
satisfying (A1)–(A4), and let  be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let
be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let  be a finite family of quasi-nonexpansive and
be a finite family of quasi-nonexpansive and  -Lipschitz mappings of
-Lipschitz mappings of  into itself, and let
into itself, and let  be a
be a  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  , let
, let  a
a  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  and
and  be a maximal monotone mapping. Assume that
be a maximal monotone mapping. Assume that

Let  be the
be the  -mapping generated by
-mapping generated by  and
and  . Let
. Let  ,
,  ,
,  ,
,  and
and  be sequences generated by
be sequences generated by  ,
, 
 ,
,  and let
and let

where  satisfy the following conditions:
satisfy the following conditions:
(i) for some
for some  with
with  ;
;
(ii) ,
, 
 for some
for some  with
with  ;
;
(iii) for some
for some  with
with  .
.
Then,  and
and  converge strongly to
converge strongly to 
Proof.
In the light of the definition of the resolvent,  can be rewritten as
can be rewritten as  . Let
. Let  and using the fact
and using the fact  be a sequence of mappings defined as in Lemma 2.6,
be a sequence of mappings defined as in Lemma 2.6,  is an
is an  -inverse-strongly monotone and that
-inverse-strongly monotone and that  , where
, where  for some
for some  with
with  , we can write
, we can write

Next, we will divide the proof into six steps.
Step 1.
We first show that  is well defined and
is well defined and  is closed and convex for any
is closed and convex for any  .
.
From the assumption, we see that  is closed and convex. Suppose that
is closed and convex. Suppose that  is closed and convex for some
is closed and convex for some  . Next, we show that
. Next, we show that  is closed and convex for some
is closed and convex for some  . For any
. For any  , we obtain that
, we obtain that

is equivalent to

Thus  is closed and convex. Then,
is closed and convex. Then,  is closed and convex for any
is closed and convex for any  . This implies that
. This implies that  is well defined.
is well defined.
Step 2.
Next, we show by induction that  for each
for each  .
.
Taking  and by condition (ii), we get that
and by condition (ii), we get that  is nonexpansive for all
is nonexpansive for all  . From the assumption, we see that
. From the assumption, we see that  . Suppose
. Suppose  for some
for some  . For any
. For any  , we have
, we have

Thus, we have

It follows that  This implies that
This implies that  for each
for each  .
.
Step 3.
Next, we show that  and
and  .
.
From  , we have
, we have

for each  . Using
. Using  we also have
we also have

So, for  , we have
, we have

This implies that

From  and
and  , we obtain
, we obtain

From (3.13), we have, for 

It follows that

Thus the sequence  is a bounded and nonincreasing sequence, so
is a bounded and nonincreasing sequence, so  exists, that is,
exists, that is,

Indeed, from (3.13), we get

From (3.16), we obtain

Since  we have
we have

By (3.18), we obtain

Step 4.
Next, we show that 
For any given  ,
,  . It is easy to see that
. It is easy to see that  . As
. As  is nonexpansive, we have
is nonexpansive, we have

Similarly, we can prove that

Observe that

Substituting (3.21) into (3.23), and using conditions (i) and (ii), we have

It follows that

Since  , we obtain
, we obtain

Since the resolvent operator  is 1-inverse strongly monotone, we obtain
is 1-inverse strongly monotone, we obtain

which yields that

Similarly, we obtain

Substituting (3.28) into (3.23), and using condition (i), we have

It follows that

Applying  and
and  as
as  to the last inequality, we get
to the last inequality, we get

Note that

Substituting (3.22) into (3.33), and using conditions (i) and (ii), we have

It follows that

Since  , we obtain
, we obtain

Substituting (3.29) into (3.33), and using conditions (i) and (ii), we have

It follows that

Applying  and
and  as
as  to the last inequality, we get
to the last inequality, we get

From (3.32) and (3.39), we have

From (3.33), (3.4), and condition (iii), we have

It follows that

Since  , we obtain
, we obtain

On the other hand, in the light of Lemma 2.6(3),  is firmly nonexpansvie, so we have
is firmly nonexpansvie, so we have

which implies that

Using (3.41) again and (3.45), we have

It follows from the condition (i) that

Since  and
and  , it is implied that
, it is implied that

From (3.39) and (3.48), we have

By (3.3), we get

Since  for some
for some  with
with  , and
, and  as
as  , we also have
, we also have

From (3.40) and (3.48), we have

Furthermore, by the triangular inequality, we also have

Applying (3.51) and (3.52), we obtain

Let  be the mapping defined by (3.1). Since
be the mapping defined by (3.1). Since  is bounded, applying Lemma 3.2 and (3.54), we have
is bounded, applying Lemma 3.2 and (3.54), we have

Step 5.
Next, we show that 
Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  . Since
. Since  and
and  is closed and convex,
is closed and convex,  is weakly closed and hence
is weakly closed and hence  . From
. From  we obtain
we obtain 
-
(a)
First, we prove that
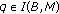 .
.
We observe that  is a
is a  -Lipschitz monotone mapping and
-Lipschitz monotone mapping and  . From Lemma 2.2, we know that
. From Lemma 2.2, we know that  is maximal monotone. Let
is maximal monotone. Let  , that is,
, that is,  . Since
. Since  , we have
, we have

that is,

By virtue of the maximal monotonicity of  , we have
, we have

and so

It follows from  ,
,  and
and  that
that

It follows from the maximal monotonicity of  that
that  , that is,
, that is,  .
.
-
(b)
Next, we show that
 . Since
. Since 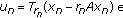 dom
dom  , we have
, we have  (3.61)
(3.61)
From (A2), we also have

And hence

For  with
with  and
and  let
let  Since
Since  and
and  we have
we have  So, from (3.63), we have
So, from (3.63), we have

Since  we have
we have  . Further, from the inverse strongly monotonicity of
. Further, from the inverse strongly monotonicity of  we have
we have  So, from (A5), the weakly lower semicontinuity of
So, from (A5), the weakly lower semicontinuity of  and
and  , we have
, we have

as  From (A1), (A4) and (3.65), we also get
From (A1), (A4) and (3.65), we also get

Letting  we have, for each
we have, for each 

This implies that 
-
(c)
Now, we prove that
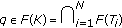 .
.
Assume  Since
Since  and we know that
and we know that  and
and  it follows by the Opial's condition (Lemma 2.4) that
it follows by the Opial's condition (Lemma 2.4) that

which is a contradiction. Thus, we get  .
.
The conclusion is  .
.
Step 6.
Finally, we show that  and
and  , where
, where 
Since  is nonempty closed convex subset of
is nonempty closed convex subset of  , there exists a unique
, there exists a unique  such that
such that  Since
Since  and
and  , we have
, we have

for all  . From (3.69),
. From (3.69),  is bounded, so
is bounded, so  . By the weak lower semicontinuity of the norm, we have
. By the weak lower semicontinuity of the norm, we have

However, Since  , we have
, we have

Using (3.69) and (3.70), we obtain  . Thus
. Thus  and
and  So, we have
So, we have

Thus, we obtain that

From  , we obtain
, we obtain  . Using the Kadec-Klee property (Lemma 2.5) of
. Using the Kadec-Klee property (Lemma 2.5) of  , we obtain that
, we obtain that

and hence  in norm. Finally, noticing
in norm. Finally, noticing  we also conclude that
we also conclude that  in norm. This completes the proof.
in norm. This completes the proof.
Corollary 3.4.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), and let
satisfying (A1)–(A4), and let  be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let
be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let  be a finite family of nonexpansive mappings of
be a finite family of nonexpansive mappings of  into itself, let
into itself, let  be a
be a  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  , let
, let  be a
be a  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  and
and  a maximal monotone mapping. Assume that
a maximal monotone mapping. Assume that

Let  be the
be the  -mapping generated by
-mapping generated by  and
and  . Let
. Let  ,
,  ,
,  ,
,  and
and  be sequences generated by (3.3) satisfying the following conditions in Theorem 3.3. Then,
be sequences generated by (3.3) satisfying the following conditions in Theorem 3.3. Then,  and
and  converge strongly to
converge strongly to 
From Theorem 3.3, we can obtain the following results.
Theorem 3.5.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4), and let
satisfying (A1)–(A4), and let  be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let
be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let  be a finite family of quasi-nonexpansive and
be a finite family of quasi-nonexpansive and  -Lipschitz mappings of
-Lipschitz mappings of  into itself, let
into itself, let  be a
be a  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  and let
and let  be a
be a  -inverse-strongly monotone mapping of
-inverse-strongly monotone mapping of  into
into  . Assume that
. Assume that

Let  be the
be the  -mapping generated by
-mapping generated by  and
and  . Let
. Let  ,
,  ,
,  ,
,  and
and  be sequences generated by
be sequences generated by  ,
, 
 ,
,  and let
and let

where  satisfy the following conditions:
satisfy the following conditions:
(i) for some
for some  with
with  ;
;
(ii) ,
, 
 for some
for some  with
with  ;
;
(iii) for some
for some  with
with  .
.
Then,  and
and  converge strongly to
converge strongly to 
Proof.
In Theorem 3.3 take  , where
, where  is the indicator function of
is the indicator function of  , that is,
, that is,

Then the variational inclusion problem (1.3) is equivalent to variational inequality problem (1.14), that is, to find  such that
such that

Again, since  , then
, then

and so we have

We can obtain the desired conclusion from Theorem 3.3 immediately.
Next, we consider another class of important nonlinear mappings: strict pseudocontractions.
Definition 3.6.
A mapping  is called strictly pseudocontraction if there exists a constant
is called strictly pseudocontraction if there exists a constant  such that
such that

If  , then
, then  is nonexpansive.
is nonexpansive.
In this case, let  a
a  -strictly pseudocontraction. Putting
-strictly pseudocontraction. Putting  , then
, then  is a
is a  -inverse-strongly monotone mapping. In fact, from (3.82) we have
-inverse-strongly monotone mapping. In fact, from (3.82) we have

Observe that

Hence, we obtain

This shows that  is
is  -inverse-strongly monotone mapping.
-inverse-strongly monotone mapping.
Now, we get the following result.
Theorem 3.7.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4) and let
satisfying (A1)–(A4) and let  be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let
be a proper lower semicontinuous and convex function with assumption (B1) or (B2). Let  be a finite family of quasi-nonexpansive and
be a finite family of quasi-nonexpansive and  -Lipschitz mappings of
-Lipschitz mappings of  into itself, let
into itself, let  be a
be a  -strictly pseudocontraction mapping of
-strictly pseudocontraction mapping of  into
into  and let
and let  be a
be a  -strictly pseudocontraction mapping of
-strictly pseudocontraction mapping of  into
into  . Assume that
. Assume that

Let  be the
be the  -mapping generated by
-mapping generated by  and
and  . Let
. Let  ,
,  ,
,  ,
,  and
and  be sequences generated by
be sequences generated by  ,
, 
 ,
,  and let
and let

where  satisfy the following conditions:
satisfy the following conditions:
(i) for some
for some  with
with  ;
;
(ii) ,
, 
 for some
for some  with
with  ;
;
(iii) for some
for some  with
with  .
.
Then,  and
and  converge strongly to
converge strongly to 
Proof.
Taking  and
and  , respectively. Then we see that
, respectively. Then we see that  is
is  -inverse-strongly monotone and
-inverse-strongly monotone and  is
is  -inverse-strongly monotone, respectively. We have
-inverse-strongly monotone, respectively. We have  and
and

By using Theorem 3.5, it is easy to obtain the desired conclusion.
References
Brézis H: Opérateur maximaux monotones. In Mathematics Studies. Volume 5. North-Holland, Amsterdam, The Netherlands; 1973.
Lemaire B: Which fixed point does the iteration method select? In Recent Advances in Optimization (Trier, 1996), Lecture Notes in Economics and Mathematical Systems. Volume 452. Springer, Berlin, Germany; 1997:154–167.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63(1–4):123–145.
Chadli O, Schaible S, Yao JC: Regularized equilibrium problems with application to noncoercive hemivariational inequalities. Journal of Optimization Theory and Applications 2004, 121(3):571–596.
Chadli O, Wong NC, Yao JC: Equilibrium problems with applications to eigenvalue problems. Journal of Optimization Theory and Applications 2003, 117(2):245–266. 10.1023/A:1023627606067
Konnov IV, Schaible S, Yao JC: Combined relaxation method for mixed equilibrium problems. Journal of Optimization Theory and Applications 2005, 126(2):309–322. 10.1007/s10957-005-4716-0
Moudafi A, Théra M: Proximal and dynamical approaches to equilibrium problems. In Ill-Posed Variational Problems and Regularization Techniques (Trier, 1998), Lecture Notes in Economics and Mathematical Systems. Volume 477. Springer, Berlin, Germany; 1999:187–201.
Zeng L-C, Wu S-Y, Yao J-C: Generalized KKM theorem with applications to generalized minimax inequalities and generalized equilibrium problems. Taiwanese Journal of Mathematics 2006, 10(6):1497–1514.
Ceng LC, Sahu DR, Yao JC: Implicit iterative algorithms for asymptotically nonexpansive mappings in the intermediate sense and Lipschitz-continuous monotone mappings. Journal of Computational and Applied Mathematics 2010, 233(11):2902–2915. 10.1016/j.cam.2009.11.035
Ceng L-C, Yao J-C: A relaxed extragradient-like method for a generalized mixed equilibrium problem, a general system of generalized equilibria and a fixed point problem. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(3–4):1922–1937. 10.1016/j.na.2009.09.033
Ceng LC, Petruşel A, Yao JC: Iterative approaches to solving equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Journal of Optimization Theory and Applications 2009, 143(1):37–58. 10.1007/s10957-009-9549-9
Cianciaruso F, Marino G, Muglia L, Yao Y: A hybrid projection algorithm for finding solutions of mixed equilibrium problem and variational inequality problem. Fixed Point Theory and Applications 2010, 2010:-19.
Chadli O, Liu Z, Yao JC: Applications of equilibrium problems to a class of noncoercive variational inequalities. Journal of Optimization Theory and Applications 2007, 132(1):89–110. 10.1007/s10957-006-9072-1
Cholamjiak P, Suantai S: A new hybrid algorithm for variational inclusions, generalized equilibrium problems, and a finite family of quasi-nonexpansive mappings. Fixed Point Theory and Applications 2009, 2009:-20.
Jaiboon C, Kumam P: A general iterative method for addressing mixed equilibrium problems and optimization problems. Nonlinear Analysis, Theory, Methods and Applications 2010, 73: 1180–1202. 10.1016/j.na.2010.04.041
Jaiboon C, Kumam P: Strong convergence for generalized equilibrium problems, fixed point problems and relaxed cocoercive variational inequalities. Journal of Inequalities and Applications 2010, 2010:-43.
Jaiboon C, Chantarangsi W, Kumam P: A convergence theorem based on a hybrid relaxed extragradient method for generalized equilibrium problems and fixed point problems of a finite family of nonexpansive mappings. Nonlinear Analysis: Hybrid Systems 2010, 4(1):199–215. 10.1016/j.nahs.2009.09.009
Kumam P, Jaiboon C: A new hybrid iterative method for mixed equilibrium problems and variational inequality problem for relaxed cocoercive mappings with application to optimization problems. Nonlinear Analysis: Hybrid Systems 2009, 3(4):510–530. 10.1016/j.nahs.2009.04.001
Peng J-W, Yao J-C: A new hybrid-extragradient method for generalized mixed equilibrium problems, fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2008, 12(6):1401–1432.
Peng J-W, Yao J-C: Some new iterative algorithms for generalized mixed equilibrium problems with strict pseudo-contractions and monotone mappings. Taiwanese Journal of Mathematics 2009, 13(5):1537–1582.
Yao Y, Liou Y-C, Yao J-C: A new hybrid iterative algorithm for fixed-point problems, variational inequality problems, and mixed equilibrium problems. Fixed Point Theory and Applications 2008, 2008:-15.
Yao Y, Liou Y-C, Wu Y-J: An extragradient method for mixed equilibrium problems and fixed point problems. Fixed Point Theory and Applications 2009, 2009:-15.
Takahashi W, Takeuchi Y, Kubota R: Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2008, 341(1):276–286. 10.1016/j.jmaa.2007.09.062
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(3):1025–1033. 10.1016/j.na.2008.02.042
Zhang S-S, Lee JHW, Chan CK: Algorithms of common solutions to quasi variational inclusion and fixed point problems. Applied Mathematics and Mechanics. English Edition 2008, 29(5):571–581. 10.1007/s10483-008-0502-y
Peng J-W, Wang Y, Shyu DS, Yao J-C: Common solutions of an iterative scheme for variational inclusions, equilibrium problems, and fixed point problems. Journal of Inequalities and Applications 2008, 2008:-15.
Kumam P, Katchang P: A general iterative method of fixed points for mixed equilibrium problems and variational inclusion problems. Journal of Inequalities and Applications 2010, 2010:-25.
Acedo GL, Xu H-K: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(7):2258–2271. 10.1016/j.na.2006.08.036
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama, Japan; 2000.
Peng J-W, Liou YC, Yao JC: An iterative algorithm combining viscosity method with parallel method for a generalized equilibrium problem and strict pseudocontractions. Fixed Point Theory and Applications 2009, 2009:-21.
Atsushiba S, Takahashi W: Strong convergence theorems for a finite family of nonexpansive mappings and applications. Indian Journal of Mathematics 1999, 41(3):435–453.
Acknowledgments
The authors would like to express their thank to the referees for helpful suggestions. The first author was supported by the National Research Council of Thailand and the Faculty of Science and Technology RMUTT Research Fund. The second author was supported by Rajamangala University of Technology Rattanakosin Research and Development Institute. The third author was supported by the Thailand Research Fund and the Commission on Higher Education under Grant No. MRG5380044.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kumam, W., Jaiboon, C., Kumam, P. et al. A Shrinking Projection Method for Generalized Mixed Equilibrium Problems, Variational Inclusion Problems and a Finite Family of Quasi-Nonexpansive Mappings. J Inequal Appl 2010, 458247 (2010). https://doi.org/10.1155/2010/458247
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/458247
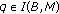 .
. . Since
. Since 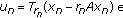 dom
dom  , we have
, we have 
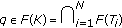 .
.