- Research Article
- Open access
- Published:
Convolution Properties of Classes of Analytic and Meromorphic Functions
Journal of Inequalities and Applications volume 2010, Article number: 385728 (2010)
Abstract
General classes of analytic functions defined by convolution with a fixed analytic function are introduced. Convolution properties of these classes which include the classical classes of starlike, convex, close-to-convex, and quasiconvex analytic functions are investigated. These classes are shown to be closed under convolution with prestarlike functions and the Bernardi-Libera integral operator. Similar results are also obtained for the classes consisting of meromorphic functions in the punctured unit disk.
1. Motivation and Definitions
Let  be the set of all analytic functions defined in the unit disk
be the set of all analytic functions defined in the unit disk  . Denote by
. Denote by  the class of normalized analytic functions
the class of normalized analytic functions  defined in
defined in  . For two functions
. For two functions  and
and  in
in  , the convolution or Hadamard product of
, the convolution or Hadamard product of  and
and  is the function
is the function  defined by
defined by  . A function
. A function  is subordinate to an analytic function
is subordinate to an analytic function  , written
, written  , if there exists a Schwarz function
, if there exists a Schwarz function  , analytic in
, analytic in  with
with  and
and  satisfying
satisfying  If the function
If the function  is univalent in
is univalent in  , then
, then  is equivalent to
is equivalent to  and
and  .
.
The classes of starlike and convex analytic functions and other related subclasses of analytic functions can be put in the form

where  is a fixed function and
is a fixed function and  is a suitably normalized function with positive real part. In particular, let
is a suitably normalized function with positive real part. In particular, let  and
and  . For
. For  ,
,  ,
,  and
and  are, respectively, the familiar classes
are, respectively, the familiar classes  of starlike functions of order
of starlike functions of order  and
and  consisting of convex functions of order
consisting of convex functions of order  . Analogous to the class
. Analogous to the class  , the class
, the class  is defined by
is defined by

Let  and
and  satisfy
satisfy

By adding the two inequalities, it is evident that the function  is starlike and hence both
is starlike and hence both  and
and  are close-to-convex and univalent. This motivates us to consider the following classes of functions.
are close-to-convex and univalent. This motivates us to consider the following classes of functions.
It is assumed in the sequel that  is a fixed integer,
is a fixed integer,  is a fixed function in
is a fixed function in  , and
, and  is a convex univalent function with positive real part in
is a convex univalent function with positive real part in  satisfying
satisfying  .
.
Definition 1.1.
The class  consists of
consists of  ,
, ,
, , satisfying
, satisfying  in
in  and the subordination
and the subordination

The class  consists of
consists of  for which
for which  . The class
. The class  consists of
consists of  for which
for which  , where
, where  and
and  . Equivalently,
. Equivalently,  if
if  satisfies the condition
satisfies the condition  in
in  and the subordination
and the subordination

The class  consists of
consists of  for which
for which  .
.
Now let  and
and  . From (1.4), it follows that
. From (1.4), it follows that

The convexity of  implies that
implies that

which shows that the function  is starlike in
is starlike in  . Thus, it follows from (1.4) that the component function
. Thus, it follows from (1.4) that the component function  of
of  is close-to-convex in
is close-to-convex in  , and hence univalent. Similarly, the component function
, and hence univalent. Similarly, the component function  of
of  is univalent.
is univalent.
If  , then the classes
, then the classes  and
and  are reduced, respectively, to
are reduced, respectively, to  and
and  introduced and investigated in [1]; these classes were denoted there by
introduced and investigated in [1]; these classes were denoted there by  and
and  , respectively. If
, respectively. If  , where
, where

then the class  coincides with the class studied in [2], which there was denoted by
coincides with the class studied in [2], which there was denoted by  , and
, and  reduces to a class introduced in [3] which there was denoted by
reduces to a class introduced in [3] which there was denoted by  . It is evident that the classes
. It is evident that the classes  and
and  extend the classical classes of starlike and convex functions, respectively.
extend the classical classes of starlike and convex functions, respectively.
Definition 1.2.
The class  consists of
consists of  ,
, ,
, , satisfying the subordination
, satisfying the subordination

for some  . In this case, we say that
. In this case, we say that  with respect to
with respect to  . The class
. The class  consists of
consists of  for which
for which  . The class
. The class  consists of
consists of  for which
for which  or equivalently satisfying the subordination
or equivalently satisfying the subordination

for some  with
with  ,
,  . In this case, we say that
. In this case, we say that  with respect to
with respect to  . The class
. The class  consists of
consists of  for which
for which  .
.
When  , the classes
, the classes  and
and  reduce, respectively, to
reduce, respectively, to  and
and  introduced and investigated in [1]. If
introduced and investigated in [1]. If  , where
, where  is defined by (1.8), then the class
is defined by (1.8), then the class  coincides with
coincides with  studied in [2]. Clearly the classes
studied in [2]. Clearly the classes  and
and  extend the classical classes of close-to-convex and quasiconvex functions, respectively.
extend the classical classes of close-to-convex and quasiconvex functions, respectively.
For  , the class
, the class  of prestarlike functions of order
of prestarlike functions of order  is defined by
is defined by

while  consists of
consists of  satisfying
satisfying  .
.
The well-known result that the classes of starlike functions of order  and convex functions of order
and convex functions of order  are closed under convolution with prestarlike functions of order
are closed under convolution with prestarlike functions of order  follows from the following.
follows from the following.
Theorem 1.3 (see [4, Theorem  ]).
]).
Let  ,
,  , and
, and  . Then
. Then

for any analytic function  , where
, where  denotes the closed convex hull of
denotes the closed convex hull of  .
.
In the following section, by using the methods of convex hull and differential subordination, convolution properties of functions belonging to the four classes  ,
,  ,
,  and
and  , are investigated. It would be evident that various earlier works, see, for example, [5–10], are special instances of our work.
, are investigated. It would be evident that various earlier works, see, for example, [5–10], are special instances of our work.
In Section 3, new subclasses of meromorphic functions are introduced. These subclasses extend the classical subclasses of meromorphic starlike, convex, close-to-convex, and quasiconvex functions. Convolution properties of these newly defined subclasses will be investigated. Simple consequences of the results obtained will include the work of Bharati and Rajagopal [6] involving the function  ,
,  , as well as the work of Al-Oboudi and Al-Zkeri [5] on the modified Salagean operator.
, as well as the work of Al-Oboudi and Al-Zkeri [5] on the modified Salagean operator.
2. Convolution of Analytic Functions
Our first result shows that the classes  and
and  are closed under convolution with prestarlike functions.
are closed under convolution with prestarlike functions.
Theorem 2.1.
Let  be a fixed integer and
be a fixed integer and  a fixed function in
a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying  ,
,  , and
, and  .
.
(1)If  , then
, then  .
.
(2)If  , then
, then  .
.
Proof.
-
(1)
It is sufficient to prove that
 whenever
whenever 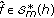 . Once this is established, the general result for
. Once this is established, the general result for  follows from the fact that
follows from the fact that 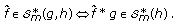 (2.1)
(2.1)
For  , define the functions
, define the functions  and
and  by
by

It will first be proved that  belongs to
belongs to  . For
. For  and
and  , clearly
, clearly

Since  is a convex domain, it follows that
is a convex domain, it follows that

or

Since  , the subordination (2.5) yields
, the subordination (2.5) yields

and hence 
A computation shows that

Since  and
and  , Theorem 1.3 yields
, Theorem 1.3 yields

and because  , we deduce that
, we deduce that

Thus  .
.
-
(2)
The function
 is in
is in 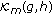 if and only if
if and only if 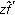 is in
is in 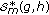 and by the first part above, it follows that
and by the first part above, it follows that  . Hence
. Hence 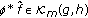 .
.
Remark 2.2.
The above theorem can be expressed in the following equivalent forms:

When  , various known results are easily obtained as special cases of Theorem 2.1. For instance, [1, Theorem
, various known results are easily obtained as special cases of Theorem 2.1. For instance, [1, Theorem  , page 336] is easily deduced from Theorem 2.1(1), while [1, Corollary
, page 336] is easily deduced from Theorem 2.1(1), while [1, Corollary  , page 336] follows from Theorem 2.1(2). If
, page 336] follows from Theorem 2.1(2). If  is defined by (1.8), then [3, Theorem
is defined by (1.8), then [3, Theorem  , page 110] follows from Theorem 2.1(1), and [3, Corollary
, page 110] follows from Theorem 2.1(1), and [3, Corollary  , page 111] follows from Theorem 2.1(2).
, page 111] follows from Theorem 2.1(2).
Corollary 2.3.
Let  be a fixed integer and
be a fixed integer and  a fixed function in
a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying  ,
,  . Define
. Define

If  , then
, then  . Similarly, if
. Similarly, if  , then
, then  .
.
Proof.
Define the function  by
by

For  , the function
, the function  is a convex function [11], and hence
is a convex function [11], and hence  ([4, Theorem
([4, Theorem  , page 49]). It is clear from the definition of
, page 49]). It is clear from the definition of  that
that

so that  . By Theorem 2.1(1), it follows that
. By Theorem 2.1(1), it follows that  .
.
The second result is proved in a similar manner.
Remark 2.4.
If  is defined by (1.8), then Corollary 2.3 reduces to [2, Theorem
is defined by (1.8), then Corollary 2.3 reduces to [2, Theorem  , page 324].
, page 324].
Theorem 2.5.
Let  be a fixed integer and
be a fixed integer and  a fixed function in
a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying 
 , and
, and  .
.
(1)If  with respect to
with respect to  , then
, then  with respect to
with respect to  .
.
(2)If  with respect to
with respect to  , then
, then  with respect to
with respect to  .
.
Proof.
-
(1)
In view of the fact that
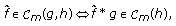 (2.14)
(2.14)
we well only prove that  when
when  . Let
. Let  . For
. For  , define the functions
, define the functions  and
and  by
by

Since  , it is evident from (2.6) that
, it is evident from (2.6) that  .
.
That  follows from Theorem 2.1(1). Now a computation shows that
follows from Theorem 2.1(1). Now a computation shows that

Since  and
and  , Theorem 1.3 yields
, Theorem 1.3 yields

and because  , it follows that
, it follows that

Thus  .
.
-
(2)
The function
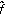 is in
is in 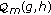 if and only if
if and only if  is in
is in 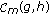 and by the first part, clearly
and by the first part, clearly 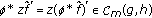 . Hence
. Hence  .
.
Remark 2.6.
Again when  , known results are easily obtained as special cases of Theorem 2.5. For instance, [1, Theorem
, known results are easily obtained as special cases of Theorem 2.5. For instance, [1, Theorem  , page 337] follows from Theorem 2.5(1), and [1, Theorem
, page 337] follows from Theorem 2.5(1), and [1, Theorem  , page 339] is a special case of Theorem 2.5(2).
, page 339] is a special case of Theorem 2.5(2).
Corollary 2.7.
Let  be a fixed integer and
be a fixed integer and  a fixed function in
a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying  ,
,  . Let
. Let  be the Bernardi-Libera integral transform of
be the Bernardi-Libera integral transform of  defined by (2.11). If
defined by (2.11). If  , then
, then  .
.
The proof is similar to the proof of Corollary 2.3 and is therefore omitted.
Remark 2.8.
If  is defined by (1.8), then Corollary 2.7 reduces to [2, Theorem
is defined by (1.8), then Corollary 2.7 reduces to [2, Theorem  , page 326].
, page 326].
3. Convolution of Meromorphic Functions
Let  denote the class of functions
denote the class of functions  of the form
of the form

that are analytic in the punctured unit disk  . The convolution of two meromorphic functions
. The convolution of two meromorphic functions  and
and  , where
, where  is given by (3.1) and
is given by (3.1) and  , is given by
, is given by

In this section, several subclasses of meromorphic functions in the punctured unit disk are introduced by means of convolution with a given fixed meromorphic function. First we take note that the familiar classes of meromorphic starlike and convex functions and other related subclasses of meromorphic functions can be put in the form

where  is a fixed function in
is a fixed function in  and
and  is a suitably normalized analytic function with positive real part. For instance, the class of meromorphic starlike functions of order
is a suitably normalized analytic function with positive real part. For instance, the class of meromorphic starlike functions of order  ,
,  , defined by
, defined by

is a particular case of  with
with  and
and  .
.
Here four classes  ,
,  ,
,  , and
, and  of meromorphic functions are introduced and the convolution properties of these new subclasses are investigated. As before, it is assumed that
of meromorphic functions are introduced and the convolution properties of these new subclasses are investigated. As before, it is assumed that  is a fixed integer,
is a fixed integer,  is a fixed function in
is a fixed function in  , and
, and  is a convex univalent function with positive real part in
is a convex univalent function with positive real part in  satisfying
satisfying  .
.
Definition 3.1.
The class  c onsists of
c onsists of  ,
, ,
, , satisfying
, satisfying  in
in  and the subordination
and the subordination

The class  consists of
consists of  for which
for which  . The class
. The class  consists of
consists of  for which
for which  or equivalently satisfying the condition
or equivalently satisfying the condition  in
in  and the subordination
and the subordination

The class  consists of
consists of  for which
for which  .
.
Various subclasses of meromorphic functions investigated in earlier works are special instances of the above defined classes. For instance, if  , then
, then  coincides with
coincides with  . By putting
. By putting  , where
, where

the class  reduces to the class
reduces to the class  investigated in [9]. If
investigated in [9]. If  , where
, where

then the class of  is the class
is the class  studied in [5]. If
studied in [5]. If  , where
, where

then the class  coincides with
coincides with  investigated in [6].
investigated in [6].
Definition 3.2.
The class  consists of
consists of  ,
, ,
, , satisfying the subordination
, satisfying the subordination

for some  . In this case, we say that
. In this case, we say that  with respect to
with respect to  . The class
. The class  consists of
consists of  for which
for which  . The class
. The class  consists of
consists of  for which
for which  or equivalently satisfying the subordination
or equivalently satisfying the subordination

for some  with
with  and
and  . The class
. The class  consists of
consists of  for which
for which  .
.
If  , then
, then  coincides with
coincides with  . If
. If  is defined by (3.8), then
is defined by (3.8), then  reduces to
reduces to  investigated in [5]. If
investigated in [5]. If  is defined by (3.9), then the class
is defined by (3.9), then the class  is the class
is the class  studied in [6].
studied in [6].
We shall require the theorem below which is a simple modification of Theorem 1.3.
Theorem 3.3.
Let  ,
,  ,
,  , and
, and  . Then, for any analytic function
. Then, for any analytic function  ,
,

Theorem 3.4.
Assume that  is a fixed integer and
is a fixed integer and  is a fixed function in
is a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying  ,
,  , and
, and  with
with  .
.
(1)If  , then
, then  .
.
(2)If  , then
, then  .
.
Proof.
-
(1)
It is enough to prove the result for
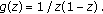 For
For  , define the functions
, define the functions  and
and 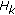 by
by 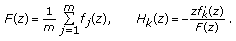 (3.13)
(3.13)
We show that  satisfies the condition
satisfies the condition  . For
. For  and
and  , clearly
, clearly

Since  is a convex domain, it follows that
is a convex domain, it follows that

or

Since  , the subordination (3.16) yields
, the subordination (3.16) yields

and thus

Inequality (3.18) shows that  .
.
A routine computation now gives

Since  and
and  , Theorem 3.3 yields
, Theorem 3.3 yields

and because  , it is clear that
, it is clear that

Thus  .
.
-
(2)
The function
 is in
is in  if and only if
if and only if 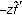 is in
is in  and the result of part (1) shows that
and the result of part (1) shows that 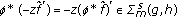 . Hence
. Hence  .
.
Remark 3.5.
-
(1)
The above theorem can be written in the following equivalent forms:
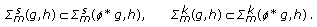 (3.22)
(3.22)
( ) When
) When  , various known results are easily obtained as special cases of Theorem 3.4. For instance, if
, various known results are easily obtained as special cases of Theorem 3.4. For instance, if  is defined by (3.7), then [9, Theorem
is defined by (3.7), then [9, Theorem  , page 1265] follows from Theorem 3.4(1).
, page 1265] follows from Theorem 3.4(1).
Corollary 3.6.
Assume that  is a fixed integer and
is a fixed integer and  is a fixed function in
is a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying  ,
,  . Define
. Define

If  , then
, then  . Similarly, if
. Similarly, if  , then
, then  .
.
Proof.
Define the function  by
by

For  , the function
, the function  is a convex function [11], and hence
is a convex function [11], and hence  ([4, Theorem
([4, Theorem  , page 49]). It is clear from the definition of
, page 49]). It is clear from the definition of  that
that

so that  . By Theorem 3.4, it follows that
. By Theorem 3.4, it follows that  .
.
The second result is established analogously.
Remark 3.7.
Again we take note of how our results extend various earlier works. If  is defined by (3.7), then [7, Proposition
is defined by (3.7), then [7, Proposition  , page 512] follows from Corollary 3.6. If
, page 512] follows from Corollary 3.6. If  is defined by (3.8), then Corollary 3.6 yields [5, Theorem
is defined by (3.8), then Corollary 3.6 yields [5, Theorem  , page 4]. If
, page 4]. If  is defined by (3.9), then Corollary 3.6 reduces to [6, Theorem
is defined by (3.9), then Corollary 3.6 reduces to [6, Theorem  , page 11].
, page 11].
Theorem 3.8.
Assume that  is a fixed integer and
is a fixed integer and  is a fixed function in
is a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying  ,
,  , and
, and  with
with  .
.
(1)If  with respect to
with respect to  , then
, then  with respect to
with respect to  .
.
(2)If  with respect to
with respect to  , then
, then  with respect to
with respect to  .
.
Proof.
-
(1)
In view of the fact that
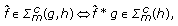 (3.26)
(3.26)
it is sufficient to prove that  when
when  . Let
. Let  . For
. For  , define the functions
, define the functions  and
and  by
by

Inequality (3.18) shows that  .
.
It is evident that

Since  and
and  , Theorem 3.3 yields
, Theorem 3.3 yields

and because  , it follows that
, it follows that

Thus  .
.
( ) The function
) The function  is in
is in  if and only if
if and only if  is in
is in  and from the first part above, it follows that
and from the first part above, it follows that  . Hence
. Hence  .
.
Corollary 3.9.
Assume that  is a fixed integer and
is a fixed integer and  is a fixed function in
is a fixed function in  . Let
. Let  be a convex univalent function satisfying
be a convex univalent function satisfying  ,
,  . Let
. Let  be defined by (3.23). If
be defined by (3.23). If  , then
, then  .
.
The proof is analogous to Corollary 2.3 and is omitted.
Remark 3.10.
If  is defined by (3.8), then Corollary 3.9 yields [5, Theorem
is defined by (3.8), then Corollary 3.9 yields [5, Theorem  , page 9]. If
, page 9]. If  is defined by (3.9), then Corollary 3.9 reduces to [6, Theorem
is defined by (3.9), then Corollary 3.9 reduces to [6, Theorem  , page 14].
, page 14].
References
Shanmugam TN: Convolution and differential subordination. International Journal of Mathematics and Mathematical Sciences 1989, 12(2):333–340. 10.1155/S0161171289000384
Padmanabhan KS, Parvatham R: Some applications of differential subordination. Bulletin of the Australian Mathematical Society 1985, 32(3):321–330. 10.1017/S0004972700002410
Padmanabhan KS, Manjini R: Certain applications of differential subordination. Publications de l'Institut Mathématique 1986, 39(53):107–118.
Ruscheweyh St: Convolutions in Geometric Function Theory, Séminaire de Mathématiques Supérieures. Volume 83. Presses de l'Université de Montréal, Montreal, Canada; 1982:168.
Al-Oboudi FM, Al-Zkeri HA: Applications of Briot-Bouquet differential subordination to some classes of meromorphic functions. Arab Journal of Mathematical Sciences 2006, 12(1):17–30.
Bharati R, Rajagopal R: Meromorphic functions and differential subordination. In New Trends in Geometric Function Theory and Applications (Madras, 1990). World Scientific, Hackensack, NJ, USA; 1991:10–17.
Cho NE, Kwon OS, Srivastava HM: Inclusion and argument properties for certain subclasses of meromorphic functions associated with a family of multiplier transformations. Journal of Mathematical Analysis and Applications 2004, 300(2):505–520. 10.1016/j.jmaa.2004.07.001
Haji Mohd M, Ali RM, Keong LS, Ravichandran V: Subclasses of meromorphic functions associated with convolution. Journal of Inequalities and Applications 2009, 2009:-10.
Piejko K, Sokół J: Subclasses of meromorphic functions associated with the Cho-Kwon-Srivastava operator. Journal of Mathematical Analysis and Applications 2008, 337(2):1261–1266. 10.1016/j.jmaa.2007.04.030
Ravichandran V: Functions starlike with respect to -ply symmetric, conjugate and symmetric conjugate points. Indian Academy of Mathematics Journal 2004, 26(1):35–45.
Ruscheweyh S: New criteria for univalent functions. Proceedings of the American Mathematical Society 1975, 49: 109–115. 10.1090/S0002-9939-1975-0367176-1
Acknowledgment
The work presented here was supported in part by research grants from Universiti Sains Malaysia and University of Delhi.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ali, R., Mahnaz, M., Ravichandran, V. et al. Convolution Properties of Classes of Analytic and Meromorphic Functions. J Inequal Appl 2010, 385728 (2010). https://doi.org/10.1155/2010/385728
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/385728
 whenever
whenever 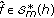 . Once this is established, the general result for
. Once this is established, the general result for  follows from the fact that
follows from the fact that 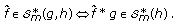
 is in
is in 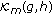 if and only if
if and only if 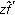 is in
is in 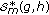 and by the first part above, it follows that
and by the first part above, it follows that  . Hence
. Hence 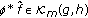 .
.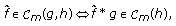
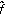 is in
is in 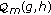 if and only if
if and only if  is in
is in 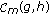 and by the first part, clearly
and by the first part, clearly 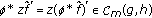 . Hence
. Hence  .
.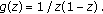 For
For  , define the functions
, define the functions  and
and 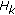 by
by 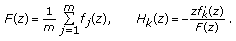
 is in
is in  if and only if
if and only if 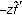 is in
is in  and the result of part (1) shows that
and the result of part (1) shows that 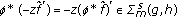 . Hence
. Hence  .
.