- Research Article
- Open access
- Published:
On Carlitz's Type  -Euler Numbers Associated with the Fermionic
-Euler Numbers Associated with the Fermionic  -Adic Integral on
-Adic Integral on 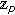
Journal of Inequalities and Applications volume 2010, Article number: 358986 (2010)
Abstract
We consider the following problem in the paper of Kim et al. (2010): "Find Witt's formula for Carlitz's type  -Euler numbers." We give Witt's formula for Carlitz's type
-Euler numbers." We give Witt's formula for Carlitz's type  -Euler numbers, which is an answer to the above problem. Moreover, we obtain a new p-adic q-l-function
-Euler numbers, which is an answer to the above problem. Moreover, we obtain a new p-adic q-l-function  for Dirichlet's character
for Dirichlet's character  , with the property that
, with the property that  for
for  using the fermionic p-adic integral on
using the fermionic p-adic integral on  .
.
1. Introduction
Throughout this paper, let  be an odd prime number. The symbol,
be an odd prime number. The symbol,  and
and  denote the rings of
denote the rings of  -adic integers, the field of
-adic integers, the field of  -adic numbers, and the field of
-adic numbers, and the field of  -adic completion of the algebraic closure of
-adic completion of the algebraic closure of  respectively. The
respectively. The  -adic absolute value in
-adic absolute value in  is normalized in such way that
is normalized in such way that  Let
Let  be the set of natural numbers and
be the set of natural numbers and 
As the definition of  -number, we use the following notations:
-number, we use the following notations:

Note that  for
for  where
where  tends to 1 in the region
tends to 1 in the region 
When one talks of  -analogue,
-analogue,  is variously considered as an indeterminate, a complex number
is variously considered as an indeterminate, a complex number  or a
or a  -adic number
-adic number  If
If  one normally assumes
one normally assumes  We will further suppose that
We will further suppose that  so that
so that  for
for  If
If  then we assume that
then we assume that 
After Carlitz [1, 2] gave  -extensions of the classical Bernoulli numbers and polynomials, the
-extensions of the classical Bernoulli numbers and polynomials, the  -extensions of Bernoulli and Euler numbers and polynomials have been studied by several authors (cf. [1–21]). The Euler numbers and polynomials have been studied by researchers in the field of number theory, mathematical physics, and so on (cf. [1, 2, 9, 11, 13–16, 22, 23]). Recently, various
-extensions of Bernoulli and Euler numbers and polynomials have been studied by several authors (cf. [1–21]). The Euler numbers and polynomials have been studied by researchers in the field of number theory, mathematical physics, and so on (cf. [1, 2, 9, 11, 13–16, 22, 23]). Recently, various  -extensions of these numbers and polynomials have been studied by many mathematicians (cf. [6–8, 10, 12, 17, 18, 20]). Also, some authors have studied in the several area of
-extensions of these numbers and polynomials have been studied by many mathematicians (cf. [6–8, 10, 12, 17, 18, 20]). Also, some authors have studied in the several area of  -theory (cf. [3, 4, 16, 19, 24]).
-theory (cf. [3, 4, 16, 19, 24]).
It is known that the generating function of Euler numbers  is given by
is given by

From (1.2), we know the recurrence formula of Euler numbers is given by

with the usual convention of replacing  by
by  (see [7, 18]).
(see [7, 18]).
In [17], the  -extension of Euler numbers
-extension of Euler numbers  are defined as
are defined as

with the usual convention of replacing  by
by 
As the same motivation of the construction in [18], Carlitz's type  -Euler numbers
-Euler numbers  are defined as
are defined as

with the usual convention of replacing  by
by  It was shown that
It was shown that  where
where  is the
is the  th Euler number. In the complex case, the generating function of Carlitz's type
th Euler number. In the complex case, the generating function of Carlitz's type  -Euler numbers
-Euler numbers  is given by
is given by

where  is a complex number with
is a complex number with  (see [18]). The remark point is that the series on the right-hand side of (1.6) is uniformly convergent in the wider sense. In
(see [18]). The remark point is that the series on the right-hand side of (1.6) is uniformly convergent in the wider sense. In  -adic case, Kim et al. [18] could not determine the generating function of Carlitz's type
-adic case, Kim et al. [18] could not determine the generating function of Carlitz's type  -Euler numbers and Witt's formula for Carlitz's type
-Euler numbers and Witt's formula for Carlitz's type  -Euler numbers.
-Euler numbers.
In this paper, we obtain the generating function of Carlitz's type  -Euler numbers in the
-Euler numbers in the  -adic case. Also, we give Witt's formula for Carlitz's type
-adic case. Also, we give Witt's formula for Carlitz's type  -Euler numbers, which is a partial answer to the problem in [18]. Moreover, we obtain a new
-Euler numbers, which is a partial answer to the problem in [18]. Moreover, we obtain a new  -adic
-adic  -
- -function
-function  for Dirichlet's character
for Dirichlet's character  with the property that
with the property that

for  using the fermionic
using the fermionic  -adic integral on
-adic integral on 
2. Carlitz's Type 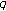 -Euler Numbers in the
-Euler Numbers in the 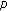 -Adic Case
-Adic Case
Let  be the space of uniformly differentiable functions on
be the space of uniformly differentiable functions on  Then, the
Then, the  -adic
-adic  -integral of a function
-integral of a function  on
on  is defined by
is defined by

(cf. [5–17, 19, 20, 22]). The bosonic  -adic integral on
-adic integral on  is considered as the limit
is considered as the limit  that is,
that is,

From (2.1), we have the fermionic  -adic integral on
-adic integral on  as follows:
as follows:

Using (2.3), we can readily derive the classical Euler polynomials,  namely
namely

In particular, when 
 is the well-known the Euler numbers (cf. [7, 16, 19]).
is the well-known the Euler numbers (cf. [7, 16, 19]).
By definition of  we show that
we show that

where  (see [7]). By (2.5) and induction, we obtain
(see [7]). By (2.5) and induction, we obtain

where  and
and  From (2.6), we note that
From (2.6), we note that

For  and any integer
and any integer  we define
we define

It is easy to see that  (see [23, page 172]). We put
(see [23, page 172]). We put  with
with  and
and  We define
We define  for
for  by
by

If we set  in (2.7), we have
in (2.7), we have

From (2.10), we note that if  then
then  hence there is no need to consider both (odd and even) cases. Thus, for each
hence there is no need to consider both (odd and even) cases. Thus, for each  we obtain
we obtain  Therefore, we have
Therefore, we have

Also, if  in (2.5), then
in (2.5), then

On the other hand, by (2.12), we obtain that

is equivalent to

From the definition of fermionic  -adic integral on
-adic integral on  and (2.11), we can derive
and (2.11), we can derive

is equivalent to

From (2.12), (2.13), (2.14), (2.15), and (2.16), it is easy to show that

where  are Carlitz's type
are Carlitz's type  -Euler numbers defined by (see [18])
-Euler numbers defined by (see [18])

Therefore, we obtain the recurrence formula for the Carlitz's type  -Euler numbers as follows:
-Euler numbers as follows:

with the usual convention of replacing  by
by  Therefore, by (2.16), (2.18), and (2.19), we obtain the following theorem, which is a partial answer to the problem in [18].
Therefore, by (2.16), (2.18), and (2.19), we obtain the following theorem, which is a partial answer to the problem in [18].
Theorem 2.1 (Witt's formula for  ).
).
For 

Carlitz's type  -Euler numbers
-Euler numbers  can be determined inductively by
can be determined inductively by

with the usual convention of replacing  by
by 
Carlitz type  -Euler polynomials
-Euler polynomials  are defined by means of the generating function
are defined by means of the generating function  as follows:
as follows:

In the cases 
 will be called Carlitz type
will be called Carlitz type  -Euler numbers (cf. [8, 19]). One also can see that the generating functions
-Euler numbers (cf. [8, 19]). One also can see that the generating functions  are determined as solutions of
are determined as solutions of

From (2.22), one gets the following.
Lemma 2.2.
(1)
(2)
It is clear from (1) and (2) of Lemma 2.2 that

From (2.24), we may state the following.
Proposition 2.3.
If  and
and  then
then
-
(1)
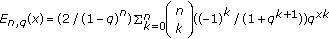 ,
, -
(2)
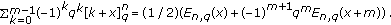
Proposition 2.4.
For  the value of
the value of  is
is  times the coefficient of
times the coefficient of  in the formal expansion of
in the formal expansion of  in powers of
in powers of  That is,
That is, 
Proof.
From (2.3), we have

which leads to

The result now follows by using (1) of Proposition 2.3.
Corollary 2.5.
If  then
then

Let  with
with  and
and  be a fixed odd prime number. One sets
be a fixed odd prime number. One sets

where  with
with  (cf. [7, 9]). Note that the natural map
(cf. [7, 9]). Note that the natural map  induces
induces

Hereafter, if  is a function on
is a function on  one denotes by the same
one denotes by the same  the function
the function  on
on  Namely one considers
Namely one considers  as a function on
as a function on 
Let  be the Dirichlet character with an odd conductor
be the Dirichlet character with an odd conductor  Then, the generalized Carlitz type
Then, the generalized Carlitz type  -Euler polynomials attached to
-Euler polynomials attached to  are defined by
are defined by

where  and
and  Then, one has the generating function of generalized Carlitz type
Then, one has the generating function of generalized Carlitz type  -Euler polynomials attached to
-Euler polynomials attached to 

Now, fixed any  with
with  and
and  From (2.31), one has
From (2.31), one has

where  and
and  with
with  By (2.31) and (2.32), one can derive
By (2.31) and (2.32), one can derive

where  and
and  with
with  Therefore, one obtains the following.
Therefore, one obtains the following.
Theorem 2.6.

where  and
and 
Let  denote the Teichmüller character mod
denote the Teichmüller character mod  For
For  one sets
one sets

Note that since 
 is defined by
is defined by  for
for  (cf. [10, 12, 21]). One notes that
(cf. [10, 12, 21]). One notes that  is analytic for
is analytic for 
One defines an interpolation function for Carlitz type  -Euler numbers. For
-Euler numbers. For 

Then,  is analytic for
is analytic for 
The values of this function at nonpositive integers are given by
Theorem 2.7.
For integers 

where  In particular, if
In particular, if  then
then 
Proof.

Therefore by (2.30), the theorem is proved.
Let  be the Dirichlet character with an odd conductor
be the Dirichlet character with an odd conductor  Let
Let  be a positive integer multiple of
be a positive integer multiple of  and
and  Then, by (2.22) and (2.31), we have
Then, by (2.22) and (2.31), we have

Therefore, we obtain the following

If  then
then  so that
so that  is a multiple of
is a multiple of  From (2.40), we derive
From (2.40), we derive

Thus, we have

By Corollary 2.5, we easily see that

From (2.42) and (2.43), we have

since  From Theorem 2.7 and (2.44), we have
From Theorem 2.7 and (2.44), we have

for  Therefore, we have the following theorem.
Therefore, we have the following theorem.
Theorem 2.8.
Let  be a positive integer multiple of
be a positive integer multiple of  and
and  and let
and let

Then,  is analytic for
is analytic for  and
and

Furthermore, for 

References
Carlitz L: q -Bernoulli numbers and polynomials. Duke Mathematical Journal 1948, 15: 987–1000. 10.1215/S0012-7094-48-01588-9
Carlitz L: q -Bernoulli and Eulerian numbers. Transactions of the American Mathematical Society 1954, 76: 332–350.
Can M, Cenkci M, Kurt V, Simsek Y: Twisted Dedekind type sums associated with Barnes' type multiple Frobenius-Euler l -functions. Advanced Studies in Contemporary Mathematics 2009, 18(2):135–160.
Cangul IN, Kurt V, Ozden H, Simsek Y: On the higher-order w - q -Genocchi numbers. Advanced Studies in Contemporary Mathematics 2009, 19(1):39–57.
Kim T: On a q -analogue of the p -adic log gamma functions and related integrals. Journal of Number Theory 1999, 76(2):320–329. 10.1006/jnth.1999.2373
Kim T: q -Volkenborn integration. Russian Journal of Mathematical Physics 2002, 9(3):288–299.
Kim T: On the analogs of Euler numbers and polynomials associated with p -adic q -integral on at . Journal of Mathematical Analysis and Applications 2007, 331(2):779–792. 10.1016/j.jmaa.2006.09.027
Kim T: On the q -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007, 326(2):1458–1465. 10.1016/j.jmaa.2006.03.037
Kim T: q -Euler numbers and polynomials associated with p -adic q -integrals. Journal of Nonlinear Mathematical Physics 2007, 14(1):15–27. 10.2991/jnmp.2007.14.1.3
Kim T: On p -adic q - l -functions and sums of powers. Journal of Mathematical Analysis and Applications 2007, 329(2):1472–1481. 10.1016/j.jmaa.2006.07.071
Kim T: On the multiple q -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008, 15(4):481–486. 10.1134/S1061920808040055
Kim T: On p -adic interpolating function for q -Euler numbers and its derivatives. Journal of Mathematical Analysis and Applications 2008, 339(1):598–608. 10.1016/j.jmaa.2007.07.027
Kim T: On a p -adic interpolation function for the q -extension of the generalized Bernoulli polynomials and its derivative. Discrete Mathematics 2009, 309(6):1593–1602. 10.1016/j.disc.2008.03.001
Kim T: Some identities on the q -Euler polynomials of higher order and q -Stirling numbers by the fermionic p -adic integral on . Russian Journal of Mathematical Physics 2009, 16(4):484–491. 10.1134/S1061920809040037
Kim T: Note on the Euler q -zeta functions. Journal of Number Theory 2009, 129(7):1798–1804. 10.1016/j.jnt.2008.10.007
Kim T: Barnes-type multiple q -zeta functions and q -Euler polynomials. Journal of Physics A: Mathematical and Theoretical 2010, 43(25):-11.
Kim T, Jang L-C, Kim Y-H, Rim S-H: New approach to q -Euler numbers and polynomials. Advances in Difference Equations 2010, 2010:-9.
Kim T, Kim Y-H, Lee B: Note on Carlitz's type q -Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society 2010, 13(2):149–155.
Ozden H, Cangul IN, Simsek Y: Multivariate interpolation functions of higher-order q -Euler numbers and their applications. Abstract and Applied Analysis 2008, 2008:-16.
Ozden H, Simsek Y, Rim S-H, Cangul IN: A note on p -adic q -Euler measure. Advanced Studies in Contemporary Mathematics 2007, 14(2):233–239.
Satoh J: q -analogue of Riemann's -function and q -Euler numbers. Journal of Number Theory 1989, 31(3):346–362. 10.1016/0022-314X(89)90078-4
Cenkci M, Simsek Y, Kurt V: Multiple two-variable p -adic q - L -function and its behavior at . Russian Journal of Mathematical Physics 2008, 15(4):447–459. 10.1134/S106192080804002X
Robert AM: A Course in p-Adic Analysis, Graduate Texts in Mathematics. Volume 198. Springer, New York, NY, USA; 2000:xvi+437.
Govil NK, Gupta V: Convergence of q -Meyer-König-Zeller-Durrmeyer operators. Advanced Studies in Contemporary Mathematics 2009, 19(1):97–108.
Acknowledgments
The first author was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (2010-0001654). The second author was supported by the research grant of Kwangwoon University in 2010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, MS., Kim, T. & Ryoo, CS. On Carlitz's Type  -Euler Numbers Associated with the Fermionic
-Euler Numbers Associated with the Fermionic  -Adic Integral on
-Adic Integral on  .
J Inequal Appl 2010, 358986 (2010). https://doi.org/10.1155/2010/358986
.
J Inequal Appl 2010, 358986 (2010). https://doi.org/10.1155/2010/358986
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/358986
 -Euler Numbers in the
-Euler Numbers in the 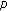 -Adic Case
-Adic Case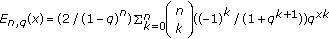 ,
,