- Research Article
- Open access
- Published:
Potential Operators in Variable Exponent Lebesgue Spaces: Two-Weight Estimates
Journal of Inequalities and Applications volume 2010, Article number: 329571 (2010)
Abstract
Two-weighted norm estimates with general weights for Hardy-type transforms and potentials in variable exponent Lebesgue spaces defined on quasimetric measure spaces  are established. In particular, we derive integral-type easily verifiable sufficient conditions governing two-weight inequalities for these operators. If exponents of Lebesgue spaces are constants, then most of the derived conditions are simultaneously necessary and sufficient for corresponding inequalities. Appropriate examples of weights are also given.
are established. In particular, we derive integral-type easily verifiable sufficient conditions governing two-weight inequalities for these operators. If exponents of Lebesgue spaces are constants, then most of the derived conditions are simultaneously necessary and sufficient for corresponding inequalities. Appropriate examples of weights are also given.
1. Introduction
We study the two-weight problem for Hardy-type and potential operators in Lebesgue spaces with nonstandard growth defined on quasimetric measure spaces  . In particular, our aim is to derive easily verifiable sufficient conditions for the boundedness of the operators
. In particular, our aim is to derive easily verifiable sufficient conditions for the boundedness of the operators

in weighted  spaces which enable us to effectively construct examples of appropriate weights. The conditions are simultaneously necessary and sufficient for corresponding inequalities when the weights are of special type and the exponent
spaces which enable us to effectively construct examples of appropriate weights. The conditions are simultaneously necessary and sufficient for corresponding inequalities when the weights are of special type and the exponent  of the space is constant. We assume that the exponent
of the space is constant. We assume that the exponent  satisfies the local log-Hölder continuity condition, and if the diameter of
satisfies the local log-Hölder continuity condition, and if the diameter of  is infinite, then we suppose that
is infinite, then we suppose that  is constant outside some ball. In the framework of variable exponent analysis such a condition first appeared in the paper [1], where the author established the boundedness of the Hardy-Littlewood maximal operator in
is constant outside some ball. In the framework of variable exponent analysis such a condition first appeared in the paper [1], where the author established the boundedness of the Hardy-Littlewood maximal operator in  . As far as we know, unfortunately, an analog of the log-Hölder decay condition (at infinity) for
. As far as we know, unfortunately, an analog of the log-Hölder decay condition (at infinity) for  is not known even in the unweighted case, which is well-known and natural for the Euclidean spaces (see [2–5]). Local log-Hölder continuity condition for the exponent
is not known even in the unweighted case, which is well-known and natural for the Euclidean spaces (see [2–5]). Local log-Hölder continuity condition for the exponent  , together with the log-Hölder decay condition, guarantees the boundedness of operators of harmonic analysis in
, together with the log-Hölder decay condition, guarantees the boundedness of operators of harmonic analysis in  spaces (see, e.g., [6]). The technique developed here enables us to expect that results similar to those of this paper can be obtained also for other integral operators, for instance, for maximal and Calderón-Zygmund singular operators defined on
spaces (see, e.g., [6]). The technique developed here enables us to expect that results similar to those of this paper can be obtained also for other integral operators, for instance, for maximal and Calderón-Zygmund singular operators defined on  .
.
Considerable interest of researchers is focused on the study of mapping properties of integral operators defined on (quasi)metric measure spaces. Such spaces with doubling measure and all their generalities naturally arise when studying boundary value problems for partial differential equations with variable coefficients, for instance, when the quasimetric might be induced by a differential operator or tailored to fit kernels of integral operators. The problem of the boundedness of integral operators naturally arises also in the Lebesgue spaces with nonstandard growth. Historically the boundedness of the maximal and fractional integral operators in  spaces was derived in the papers [7–14]. Weighted inequalities for classical operators in
spaces was derived in the papers [7–14]. Weighted inequalities for classical operators in  spaces, where
spaces, where  is a power-type weight, were established in the papers [10–12, 15–19], while the same problems with general weights for Hardy, maximal, and fractional integral operators were studied in [10, 20–25]. Moreover, in the latter paper, a complete solution of the one-weight problem for maximal functions defined on Euclidean spaces is given in terms of Muckenhoupt-type conditions.
is a power-type weight, were established in the papers [10–12, 15–19], while the same problems with general weights for Hardy, maximal, and fractional integral operators were studied in [10, 20–25]. Moreover, in the latter paper, a complete solution of the one-weight problem for maximal functions defined on Euclidean spaces is given in terms of Muckenhoupt-type conditions.
It should be emphasized that in the classical Lebesgue spaces the two-weight problem for fractional integrals is already solved (see [26, 27]), but it is often useful to construct concrete examples of weights from transparent and easily verifiable conditions.
To derive two-weight estimates for potential operators, we use the appropriate inequalities for Hardy-type transforms on  (which are also derived in this paper) and Hardy-Littlewood-Sobolev-type inequalities for
(which are also derived in this paper) and Hardy-Littlewood-Sobolev-type inequalities for  and
and  in
in  spaces.
spaces.
The paper is organized as follows: in Section 1, we give some definitions and prove auxiliary results regarding quasimetric measure spaces and the variable exponent Lebesgue spaces; Section 2 is devoted to the sufficient governing two-weight inequalities for Hardy-type operators defined on quasimetric measure spaces, while in Section 3 we study the two-weight problem for potentials defined on  .
.
Finally we point out that constants (often different constants in the same series of inequalities) will generally be denoted by  or
or  . The symbol
. The symbol  means that there are positive constants
means that there are positive constants  and
and  independent of
independent of  such that the inequality
such that the inequality  holds. Throughout the paper is denoted the function
holds. Throughout the paper is denoted the function  by the symbol
by the symbol  .
.
2. Preliminaries
Let  be a topological space with a complete measure
be a topological space with a complete measure  such that the space of compactly supported continuous functions is dense in
such that the space of compactly supported continuous functions is dense in  and there exists a nonnegative real-valued function (quasimetric)
and there exists a nonnegative real-valued function (quasimetric)  on
on  satisfying the conditions:
satisfying the conditions:
(i) if and only if
if and only if  ;
;
(ii)there exists a constant  , such that
, such that  for all
for all  ;
;
(iii)there exists a constant  , such that
, such that  for all
for all  .
.
We assume that the balls  are measurable and
are measurable and  for all
for all  and
and  ; for every neighborhood
; for every neighborhood  of
of  , there exists
, there exists  , such that
, such that  . Throughout the paper we also suppose that
. Throughout the paper we also suppose that  and that
and that

for all  , positive
, positive  and
and  with
with  , where
, where

We call the triple  a quasimetric measure space. If
a quasimetric measure space. If  satisfies the doubling condition
satisfies the doubling condition  , where the positive constant
, where the positive constant  does not depend on
does not depend on  and
and  , then
, then  is called a space of homogeneous type (SHT). For the definition, examples, and some properties of an SHT see, for example, monographs [28–30].
is called a space of homogeneous type (SHT). For the definition, examples, and some properties of an SHT see, for example, monographs [28–30].
A quasimetric measure space, where the doubling condition is not assumed, is called a nonhomogeneous space.
Notice that the condition  implies that
implies that  because we assumed that every ball in
because we assumed that every ball in  has a finite measure.
has a finite measure.
We say that the measure  is upper Ahlfors
is upper Ahlfors  -regular if there is a positive constant
-regular if there is a positive constant  such that
such that  for for all
for for all  and
and  . Further,
. Further,  is lower Ahlfors
is lower Ahlfors  -regular if there is a positive constant
-regular if there is a positive constant  such that
such that  for all
for all  and
and  . It is easy to check that if
. It is easy to check that if  is a quasimetric measure space and
is a quasimetric measure space and  , then
, then  is lower Ahlfors regular (see also, e.g., [8] for the case when
is lower Ahlfors regular (see also, e.g., [8] for the case when  is a metric).
is a metric).
For the boundedness of potential operators in weighted Lebesgue spaces with constant exponents on nonhomogeneous spaces we refer, for example, to the monograph [31, Chapter 6] and references cited therein.
Let  be a nonnegative
be a nonnegative  -measurable function on
-measurable function on  . Suppose that
. Suppose that  is a
is a  -measurable set in
-measurable set in  . We use the following notation:
. We use the following notation:

Assume that  . The variable exponent Lebesgue space
. The variable exponent Lebesgue space  (sometimes it is denoted by
(sometimes it is denoted by  ) is the class of all
) is the class of all  -measurable functions
-measurable functions  on
on  for which
for which  . The norm in
. The norm in  is defined as follows:
is defined as follows:

It is known (see, e.g., [8, 15, 32, 33]) that  is a Banach space. For other properties of
is a Banach space. For other properties of  spaces we refer, for example, to [32–34].
spaces we refer, for example, to [32–34].
We need some definitions for the exponent  which will be useful to derive the main results of the paper.
which will be useful to derive the main results of the paper.
Definition 2.1.
Let  be a quasimetric measure space and let
be a quasimetric measure space and let  be a constant. Suppose that
be a constant. Suppose that  satisfies the condition
satisfies the condition  . We say that
. We say that  belongs to the class
belongs to the class  , where
, where  , if there are positive constants
, if there are positive constants  and
and  (which might be depended on
(which might be depended on  ) such that
) such that

holds for all  ,
,  . Further,
. Further,  if there are positive constants
if there are positive constants  and
and  such that (2.5) holds for all
such that (2.5) holds for all  and all
and all  satisfying the condition
satisfying the condition  .
.
Definition 2.2.
Let  be an SHT. Suppose that
be an SHT. Suppose that  . We say that
. We say that  (
( satisfies the log-Hölder-type condition at a point
satisfies the log-Hölder-type condition at a point  ) if there are positive constants
) if there are positive constants  and
and  (which might be depended on
(which might be depended on  ) such that
) such that

holds for all  satisfying the condition
satisfying the condition  . Further,
. Further,  (
( satisfies the log-Hölder type condition on
satisfies the log-Hölder type condition on  ) if there are positive constants
) if there are positive constants  and
and  such that (2.6) holds for all
such that (2.6) holds for all  with
with  .
.
We will also need another form of the log-Hölder continuity condition given by the following definition.
Definition 2.3.
Let  be a quasimetric measure space, and let
be a quasimetric measure space, and let  . We say that
. We say that  if there are positive constants
if there are positive constants  and
and  (which might be depended on
(which might be depended on  ) such that
) such that

for all  with
with  . Further,
. Further,  if (2.7) holds for all
if (2.7) holds for all  with
with  .
.
It is easy to see that if a measure  is upper Ahlfors
is upper Ahlfors  -regular and
-regular and  (resp.,
(resp.,  ), then
), then  (resp.,
(resp.,  . Further, if
. Further, if  is lower Ahlfors
is lower Ahlfors  -regular and
-regular and  (resp.,
(resp.,  ), then
), then  (resp.,
(resp.,  ).
).
Remark 2.4.
It can be checked easily that if  is an SHT, then
is an SHT, then  .
.
Remark 2.5.
Let  be an SHT with
be an SHT with  . It is known (see, e.g., [8, 35]) that if
. It is known (see, e.g., [8, 35]) that if  , then
, then  . Further, if
. Further, if  is upper Ahlfors
is upper Ahlfors  -regular, then the condition
-regular, then the condition  implies that
implies that  .
.
Proposition 2.6.
Let  be positive and let
be positive and let  and
and  (resp.,
(resp.,  , then the functions
, then the functions  , and
, and  belong to
belong to 
 resp.,
resp.,  . Further if
. Further if  resp.,
resp.,  then
then  , and
, and  belong to
belong to  resp.,
resp.,  .
.
The proof of the latter statement can be checked immediately using the definitions of the classes  ,
,  ,
,  , and
, and  .
.
Proposition 2.7.
Let  be an
be an  and let
and let  . Then
. Then  for all
for all  with
with  , where
, where  is a small constant, and the constant
is a small constant, and the constant  does not depend on
does not depend on  .
.
Proof.
Due to the doubling condition for  , Remark 1.1, the condition
, Remark 1.1, the condition  and the fact that
and the fact that  we have the following estimates:
we have the following estimates: 
 , which proves the statement.
, which proves the statement.
The proof of the next statement is trivial and follows directly from the definition of the classes  and
and  . Details are omitted.
. Details are omitted.
Proposition 2.8.
Let  be a quasimetric measure space and let
be a quasimetric measure space and let  . Suppose that
. Suppose that  be a constant. Then the following statements hold:
be a constant. Then the following statements hold:
-
(i)
if
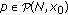 (resp.,
(resp., 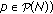 , then there are positive constants
, then there are positive constants 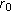 ,
, 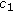 , and
, and 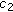 such that for all
such that for all  and all
and all 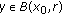 (resp., for all
(resp., for all  with
with 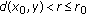 ), one has that
), one has that  .
. -
(ii)
Let
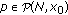 , then there are positive constants
, then there are positive constants  ,
, 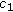 , and
, and  (in general, depending on
(in general, depending on  ) such that for all
) such that for all  (
(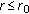 ) and all
) and all 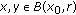 one has
one has 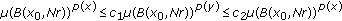 .
. -
(iii)
Let
 , then there are positive constants
, then there are positive constants  ,
, 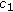 , and
, and  such that for all balls
such that for all balls 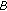 with radius
with radius  (
(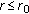 ) and all
) and all 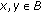 , one has that
, one has that 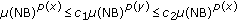 .
.
It is known that (see, e.g., [32, 33]) if  is a measurable function on
is a measurable function on  and
and  is a measurable subset of
is a measurable subset of  , then the following inequalities hold:
, then the following inequalities hold:

Further, Hölder's inequality in the variable exponent Lebesgue spaces has the following form:

Lemma 2.9.
Let  be an SHT.
be an SHT.
(i)If  is a measurable function on
is a measurable function on  such that
such that  and if
and if  is a small positive number, then there exists a positive constant
is a small positive number, then there exists a positive constant  independent of
independent of  and
and  such that
such that

(ii)Suppose that  and
and  are measurable functions on
are measurable functions on  satisfying the conditions
satisfying the conditions  and
and  . Then there exists a positive constant
. Then there exists a positive constant  such that for all
such that for all  the inequality
the inequality

holds.
Proof.
Part (i) was proved in [35] (see also [31, page 372], for constant  ). The proof of Part (ii) is given in [31, (Lemma 6.5.2, page 348)] for constant
). The proof of Part (ii) is given in [31, (Lemma 6.5.2, page 348)] for constant  and
and  , but repeating those arguments we can see that it is also true for variable
, but repeating those arguments we can see that it is also true for variable  and
and  . Details are omitted.
. Details are omitted.
Lemma 2.10.
Let  be an
be an  . Suppose that
. Suppose that  , then
, then  satisfies the condition
satisfies the condition  (resp.,
(resp.,  ) if and only if
) if and only if 
 resp.,
resp.,  .
.
Proof.
We follow [1].
Necessity.
Let  , and let
, and let  with
with  for some positive constant
for some positive constant  . Observe that
. Observe that  , where
, where  . By the doubling condition for
. By the doubling condition for  , we have that
, we have that  , where
, where  is a positive constant which is greater than 1. Taking now the logarithm in the last inequality, we have that
is a positive constant which is greater than 1. Taking now the logarithm in the last inequality, we have that  . If
. If  , then by the same arguments we find that
, then by the same arguments we find that  .
.
Sufficiency.
Let  . First observe that If
. First observe that If  , then
, then  . Consequently, this inequality and the condition
. Consequently, this inequality and the condition  yield
yield  . Further, there exists
. Further, there exists  such that
such that  and
and  , where
, where  and
and  are positive constants. Hence
are positive constants. Hence 
 .
.
Let, now,  and let
and let  where
where  is a small number. We have that
is a small number. We have that  and
and  for some positive constant
for some positive constant  . Consequently,
. Consequently,

Definition 2.11.
A measure  on
on  is said to satisfy the reverse doubling condition
is said to satisfy the reverse doubling condition  if there exist constants
if there exist constants  and
and  such that the inequality
such that the inequality  holds.
holds.
Remark 2.12.
It is known that if all annulus in  are not empty (i.e., condition (2.1) holds), then
are not empty (i.e., condition (2.1) holds), then  implies that
implies that  (see, e.g., [28, page 11, Lemma 20]).
(see, e.g., [28, page 11, Lemma 20]).
Lemma 2.13.
Let  be an
be an  . Suppose that there is a point
. Suppose that there is a point  such that
such that  . Let
. Let  be the constant defined in Definition 2.11. Then there exist positive constants
be the constant defined in Definition 2.11. Then there exist positive constants  and
and  (which might be depended on
(which might be depended on  ) such that for all
) such that for all  , the inequality
, the inequality

holds, where  and the constant
and the constant  is independent of
is independent of  .
.
Proof.
Taking into account condition (2.1) and Remark 2.12, we have that  . Let
. Let  . By the doubling and reverse doubling conditions, we have that
. By the doubling and reverse doubling conditions, we have that  . Suppose that
. Suppose that  , where
, where  is a sufficiently small constant. Then by using Lemma 2.10 we find that
is a sufficiently small constant. Then by using Lemma 2.10 we find that  .
.
In the sequel we will use the notation:

where the constants  and
and  are taken, respectively, from Definition 2.11 and the triangle inequality for the quasimetric
are taken, respectively, from Definition 2.11 and the triangle inequality for the quasimetric  , and
, and  is a diameter of
is a diameter of  .
.
Lemma 2.14.
Let  be an
be an  and let
and let  . Suppose that there is a point
. Suppose that there is a point  such that
such that  . Assume that if
. Assume that if  , then
, then  and
and  outside some ball
outside some ball  . Then there exists a positive constant C such that
. Then there exists a positive constant C such that

for all  and
and  .
.
Proof.
Suppose that  . To prove the lemma, first observe that
. To prove the lemma, first observe that  and
and  . This holds because
. This holds because  satisfies the reverse doubling condition and, consequently,
satisfies the reverse doubling condition and, consequently,

Moreover, the doubling condition yields  , where
, where  . Hence,
. Hence,  .
.
Further, since we can assume that  , we find that
, we find that

Moreover, using the doubling condition for  we have that
we have that 
 . This gives the estimates
. This gives the estimates 
 .
.
For simplicity, assume that  . Suppose that
. Suppose that  is an integer such that
is an integer such that  . Let us split the sum as follows:
. Let us split the sum as follows:

Since  outside the ball
outside the ball  , by using Hölder's inequality and the fact that
, by using Hölder's inequality and the fact that  , we have
, we have

Let us estimate  . Suppose that
. Suppose that  and
and  . Also, by Proposition 2.6, we have that
. Also, by Proposition 2.6, we have that  . Therefore, by Lemma 2.13 and the fact that
. Therefore, by Lemma 2.13 and the fact that  , we obtain that
, we obtain that  and
and  , where
, where  . Further, observe that these estimates and Hölder's inequality yield the following chain of inequalities:
. Further, observe that these estimates and Hölder's inequality yield the following chain of inequalities:

Now we claim that  , where
, where

and the positive constant  does not depend on
does not depend on  . Indeed, suppose that
. Indeed, suppose that  . Then taking into account Lemma 2.13 we have that
. Then taking into account Lemma 2.13 we have that

Consequently, since  and
and  , we find that
, we find that

This implies that  . Thus, the desired inequality is proved. Further, let us introduce the following function:
. Thus, the desired inequality is proved. Further, let us introduce the following function:

It is clear that  because
because  . Hence
. Hence

for some positive constant  . Then, by using this inequality, the definition of the function
. Then, by using this inequality, the definition of the function  , the condition
, the condition  , and the obvious estimate
, and the obvious estimate  , we find that
, we find that

Consequently,  . Hence,
. Hence,  . Analogously taking into account the fact that
. Analogously taking into account the fact that  and arguing as above, we find that
and arguing as above, we find that  . Thus, summarizing these estimates we conclude that
. Thus, summarizing these estimates we conclude that

Lemma 2.14 for  spaces defined with respect to the Lebesgue measure was derived in [24] (see also [22] for
spaces defined with respect to the Lebesgue measure was derived in [24] (see also [22] for  ,
,  , and
, and  ).
).
3. Hardy-Type Transforms
In this section, we derive two-weight estimates for the operators:

Let  be a positive constant, and let
be a positive constant, and let  be a measurable function defined on
be a measurable function defined on  . Let us introduce the notation:
. Let us introduce the notation:

Remark 3.1.
If we deal with a quasimetric measure space with  , then we will assume that
, then we will assume that  . Obviously,
. Obviously,  and
and  in this case.
in this case.
Theorem 3.2.
Let  be a quasimetric measure space. Assume that
be a quasimetric measure space. Assume that  and
and  are measurable functions on
are measurable functions on  satisfying the condition
satisfying the condition  . In the case when
. In the case when  , suppose that
, suppose that  const,
const,  const, outside some ball
const, outside some ball  . If the condition
. If the condition

holds, then  is bounded from
is bounded from  to
to  .
.
Proof.
Here we use the arguments of the proofs of Theorem 1.1.4 in [31, (see page 7)] and of Theorem 2.1 in [21]. First, we notice that  for all
for all  . Let
. Let  and let
and let  . First, assume that
. First, assume that  . We denote
. We denote

Suppose that  , then
, then  for some
for some  . Let us denote
. Let us denote  , and
, and  . Then
. Then  is a nondecreasing sequence. It is easy to check that
is a nondecreasing sequence. It is easy to check that  for
for  , and
, and  . If
. If  , then
, then  if and only if
if and only if  . If
. If  , then we take
, then we take  . Since
. Since  for every
for every  , we have that
, we have that  . It is obvious that
. It is obvious that  . Further, we have that
. Further, we have that

Let us denote

Notice that  . Consequently, by this estimate and Hölder's inequality with respect to the exponent
. Consequently, by this estimate and Hölder's inequality with respect to the exponent  we find that
we find that

where

Observe now that  . Hence, this fact and the condition
. Hence, this fact and the condition  imply that
imply that

It follows now that

Since  , it is obvious that
, it is obvious that

Finally,  . Thus,
. Thus,  is bounded if
is bounded if  .
.
Let us now suppose that  . We have
. We have

By using the already proved result for  and the fact that
and the fact that  , we find that
, we find that  because
because

Further, observe that

It is easy to see that (see also [31, Theorems 1.1.3 or 1.1.4]) the condition

guarantees the boundedness of the operator

from  to
to  . Thus,
. Thus,  is bounded. It remains to prove that
is bounded. It remains to prove that  is bounded. We have
is bounded. We have

Observe, now, that the condition  guarantees that the integral
guarantees that the integral

is finite. Moreover,  . Indeed, we have that
. Indeed, we have that

Further,

For  , we have that
, we have that  . Since
. Since  and condition (2.1) holds, there exists a point
and condition (2.1) holds, there exists a point  such that
such that  . Consequently,
. Consequently,  and
and  , where
, where  . Consequently, the condition
. Consequently, the condition  yields
yields  . Finally, we have that
. Finally, we have that  . Hence,
. Hence,  is bounded from
is bounded from  to
to  .
.
The proof of the following statement is similar to that of Theorem 3.2; therefore, we omit it (see also the proofs of Theorem 1.1.3 in [31] and Theorems 2.6 and 2.7 in [21] for similar arguments).
Theorem 3.3.
Let  be a quasimetric measure space. Assume that
be a quasimetric measure space. Assume that  and
and  are measurable functions on
are measurable functions on  satisfying the condition
satisfying the condition  . If
. If  , then, one assumes that
, then, one assumes that  const,
const,  const outside some ball
const outside some ball  . If
. If

then  is bounded from
is bounded from  to
to  .
.
Remark 3.4.
If  const, then the condition
const, then the condition  in Theorem 3.2 (resp.,
in Theorem 3.2 (resp.,  in Theorem 3.3) is also necessary for the boundedness of
in Theorem 3.3) is also necessary for the boundedness of  (resp.,
(resp.,  ) from
) from  to
to  . See [31, pages 4-5] for the details.
. See [31, pages 4-5] for the details.
4. Potentials
In this section, we discuss two-weight estimates for the potential operators  and
and  on quasimetric measure spaces, where
on quasimetric measure spaces, where  . If
. If  , then we denote
, then we denote  and
and  by
by  and
and  , respectively.
, respectively.
The boundedness of Riesz potential operators in  spaces, where
spaces, where  is a domain in
is a domain in  was established in [5, 6, 36, 37].
was established in [5, 6, 36, 37].
For the following statement we refer to [11].
Theorem A..
Let  be an
be an  . Suppose that
. Suppose that  and
and  . Assume that if
. Assume that if  , then
, then  outside some ball. Let
outside some ball. Let  be a constant satisfying the condition
be a constant satisfying the condition  . One sets
. One sets  . Then,
. Then,  is bounded from
is bounded from  to
to  .
.
Theorem B (see [9]).
Let  be a nonhomogeneous space with
be a nonhomogeneous space with  and let
and let  be a constant defined by
be a constant defined by  , where the constants
, where the constants  and
and  are taken from the definition of the quasimetric
are taken from the definition of the quasimetric  . Suppose that
. Suppose that  and that
and that  is upper Ahlfors 1-regular. One defines
is upper Ahlfors 1-regular. One defines  , where
, where  . Then
. Then  is bounded from
is bounded from  to
to  .
.
For the statements and their proofs of this section, we keep the notation of the previous sections and, in addition, introduce the new notation:

where  and
and  are constants defined in Definition 2.11 and the triangle inequality for
are constants defined in Definition 2.11 and the triangle inequality for  , respectively. We begin this section with the following general-type statement.
, respectively. We begin this section with the following general-type statement.
Theorem 4.1.
Let  be an SHT without atoms. Suppose that
be an SHT without atoms. Suppose that  and
and  is a constant satisfying the condition
is a constant satisfying the condition  . Let
. Let  . One sets
. One sets  . Further, if
. Further, if  , then one assumes that
, then one assumes that  const outside some ball
const outside some ball  . Then the inequality
. Then the inequality

holds if the following three conditions are satisfied:
(a) is bounded from
is bounded from  to
to  ;
;
(b) is bounded from
is bounded from  to
to  ;
;
(c)there is a positive constant  such that one of the following inequalities hold: (1)
such that one of the following inequalities hold: (1) for
for  a.e.
a.e.  ; (2)
; (2)  for
for  a.e.
a.e.  .
.
Proof.
For simplicity, suppose that  . The proof for the case
. The proof for the case  is similar to that of the previous case. Recall that the sets
is similar to that of the previous case. Recall that the sets  and
and  are defined in Section 2. Let
are defined in Section 2. Let  and let
and let  . We have
. We have

where  .
.
Observe that if  and
and  , then
, then  . Consequently, the triangle inequality for
. Consequently, the triangle inequality for  yields
yields  , where
, where  . Hence, by using Remark 2.4, we find that
. Hence, by using Remark 2.4, we find that  . Applying condition (a) now, we have that
. Applying condition (a) now, we have that

Further, observe that if  and
and  , then
, then  . By condition (b), we find that
. By condition (b), we find that  .
.
Now we estimate  . Suppose that
. Suppose that  . Theorem A and Lemma 2.14 yield
. Theorem A and Lemma 2.14 yield

The estimate of  for the case when
for the case when  is similar to that of the previous one. Details are omitted.
is similar to that of the previous one. Details are omitted.
Theorems 4.1, 3.2, and 3.3 imply the following statement.
Theorem 4.2.
Let  be an SHT. Suppose that
be an SHT. Suppose that  and
and  is a constant satisfying the condition
is a constant satisfying the condition  . Let
. Let  . One sets
. One sets  . If
. If  , then, one supposes that
, then, one supposes that  const outside some ball
const outside some ball  . Then inequality (4.2) holds if the following three conditions are satisfied:
. Then inequality (4.2) holds if the following three conditions are satisfied:
-
(i)
 (4.6)
(4.6)
-
(ii)
 (4.7)
(4.7)
-
(iii)
condition (c) of Theorem 4.1 holds.
Remark 4.3.
If  const on
const on  , then the conditions
, then the conditions  ,
,  , are necessary for (4.2). Necessity of the condition
, are necessary for (4.2). Necessity of the condition  follows by taking the test function
follows by taking the test function  in (4.2) and observing that
in (4.2) and observing that  for those
for those  and
and  which satisfy the conditions
which satisfy the conditions  and
and  (see also [31, Theorem 6.6.1, page 418] for the similar arguments) while necessity of the condition
(see also [31, Theorem 6.6.1, page 418] for the similar arguments) while necessity of the condition  can be derived by choosing the test function
can be derived by choosing the test function  and taking into account the estimate
and taking into account the estimate  for
for  and
and  .
.
The next statement follows in the same manner as the previous one. In this case, Theorem B is used instead of Theorem A. The proof is omitted.
Theorem 4.4.
Let  be a nonhomogeneous space with
be a nonhomogeneous space with  . Let
. Let  be a constant defined by
be a constant defined by  . Suppose that
. Suppose that  and that
and that  is upper Ahlfors 1-regular. We define
is upper Ahlfors 1-regular. We define  , where
, where  . Then the inequality
. Then the inequality

holds if
-
(i)
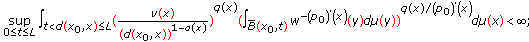 (4.9)
(4.9)
-
(ii)
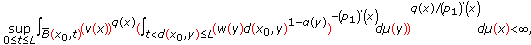 (4.10)
(4.10)
and (iii) condition (c) of Theorem 4.1 is satisfied.
Remark 4.5.
It is easy to check that if  and
and  are constants, then conditions (i) and (ii) in Theorem 4.4 are also necessary for (4.8). This follows easily by choosing appropriate test functions in (4.8) (see also Remark 4.3).
are constants, then conditions (i) and (ii) in Theorem 4.4 are also necessary for (4.8). This follows easily by choosing appropriate test functions in (4.8) (see also Remark 4.3).
Theorem 4.6.
Let  be an SHT without atoms. Let
be an SHT without atoms. Let  and let
and let  be a constant with the condition
be a constant with the condition  . One sets
. One sets  . Assume that
. Assume that  has a minimum at
has a minimum at  and that
and that  . Suppose also that if
. Suppose also that if  , then
, then  is constant outside some ball
is constant outside some ball  . Let
. Let  and
and  be positive increasing functions on
be positive increasing functions on  . Then the inequality
. Then the inequality

holds if

for  ;
;

for  .
.
Proof.
We prove the theorem for  . The proof for the case when
. The proof for the case when  is similar. Observe that by Lemma 2.10 the condition
is similar. Observe that by Lemma 2.10 the condition  implies
implies  . We will show that the condition
. We will show that the condition  implies the inequality
implies the inequality  for all
for all  , where
, where  and
and  are constants defined in Definition 2.11 and the triangle inequality for
are constants defined in Definition 2.11 and the triangle inequality for  , respectively. Indeed, let us assume that
, respectively. Indeed, let us assume that  , where
, where  is a small positive constant. Then, taking into account the monotonicity of
is a small positive constant. Then, taking into account the monotonicity of  and
and  and the facts that
and the facts that  (for small
(for small  ) and
) and  , we have
, we have

Hence,  . Further, if
. Further, if  , where
, where  is a large number, then since
is a large number, then since  and
and  are constants, for
are constants, for  , we have that
, we have that

In the last inequality we used the fact that  satisfies the reverse doubling condition.
satisfies the reverse doubling condition.
Now we show that the condition  implies
implies

Due to monotonicity of functions  and
and  , the condition
, the condition  , Proposition 2.6, Lemmas 2.9 and 2.10, and the assumption that
, Proposition 2.6, Lemmas 2.9 and 2.10, and the assumption that  has a minimum at
has a minimum at  , we find that for all
, we find that for all  ,
,

Now, Theorem 4.2 completes the proof.
Theorem 4.7.
Let  be an SHT with
be an SHT with  . Suppose that
. Suppose that  ,
,  and
and  are measurable functions on
are measurable functions on  satisfying the conditions:
satisfying the conditions:  and
and  . Assume that
. Assume that  and there is a point
and there is a point  such that
such that  . Suppose also that
. Suppose also that  is a positive increasing function on
is a positive increasing function on  . Then the inequality
. Then the inequality

holds if the following two conditions are satisfied:

Proof.
For simplicity, assume that  . First observe that by Lemma 2.10 we have
. First observe that by Lemma 2.10 we have  and
and  . Suppose that
. Suppose that  and
and  . We will show that
. We will show that  .
.
We have

First, observe that by virtue of the doubling condition for  , Remark 2.4, and simple calculation we find that
, Remark 2.4, and simple calculation we find that  . Taking into account this estimate and Theorem 3.2 we have that
. Taking into account this estimate and Theorem 3.2 we have that

Further, it is easy to see that if  , then the triangle inequality for
, then the triangle inequality for  and the doubling condition for
and the doubling condition for  yield that
yield that  . Hence, due to Proposition 2.7, we see that
. Hence, due to Proposition 2.7, we see that  for such
for such  and
and  . Therefore, Theorem 3.3 implies that
. Therefore, Theorem 3.3 implies that  .
.
It remains to estimate  . Let us denote:
. Let us denote:

Then we have that

Using Hölder's inequality for the classical Lebesgue spaces we find that

Denote the first inner integral by  and the second one by
and the second one by  .
.
By using the fact that  , where
, where  , we see that
, we see that 
 , while by applying Lemma 2.9, for
, while by applying Lemma 2.9, for  , we have that
, we have that

Summarizing these estimates for  and
and  we conclude that
we conclude that

By applying monotonicity of  , the reverse doubling property for
, the reverse doubling property for  with the constants
with the constants  and
and  (see Remark 2.12), and the condition
(see Remark 2.12), and the condition  we have that
we have that

Due to the facts that  and
and  is increasing, for
is increasing, for  , we find that
, we find that

Analogously, the estimate for  follows. In this case, we use the condition
follows. In this case, we use the condition  and the fact that
and the fact that  when
when  . The details are omitted. The theorem is proved.
. The details are omitted. The theorem is proved.
Taking into account the proof of Theorem 4.6, we can easily derive the following statement, proof of which is omitted.
Theorem 4.8.
Let  be an SHT with
be an SHT with  . Suppose that
. Suppose that  ,
,  and
and  are measurable functions on
are measurable functions on  satisfying the conditions
satisfying the conditions  and
and  . Assume that
. Assume that  . Suppose also that there is a point
. Suppose also that there is a point  such that
such that  and
and  has a minimum at
has a minimum at  . Let
. Let  and
and  be a positive increasing function on
be a positive increasing function on  satisfying the condition
satisfying the condition  (see Theorem 4.6). Then inequality (4.11) is fulfilled.
(see Theorem 4.6). Then inequality (4.11) is fulfilled.
Theorem 4.9.
Let  be an SHT with
be an SHT with  and let
and let  be upper Ahlfors 1-regular. Suppose that
be upper Ahlfors 1-regular. Suppose that  and that
and that  . Let
. Let  have a minimum at
have a minimum at  . Assume that
. Assume that  is constant satisfying the condition
is constant satisfying the condition  . We set
. We set  . If
. If  and
and  are positive increasing functions on
are positive increasing functions on  satisfying the condition
satisfying the condition

then the inequality

holds.
Proof.
The proof is similar to that of Theorem 4.6, we only discuss some details. First, observe that due to Remark 2.5 we have that  , where
, where  . It is easy to check that the condition
. It is easy to check that the condition  implies that
implies that  for all t, where the constant
for all t, where the constant  is defined in Definition 2.11 and
is defined in Definition 2.11 and  is from the triangle inequality for
is from the triangle inequality for  . Further, Lemmas 2.9 and 2.10, the fact that
. Further, Lemmas 2.9 and 2.10, the fact that  has a minimum at
has a minimum at  , and the inequality
, and the inequality

where the constant  does not depend on
does not depend on  and
and  , yield that
, yield that

Theorem 4.4 completes the proof.
Example 4.10.
Let  and
and  , where
, where  and
and  are constants satisfying the condition
are constants satisfying the condition  ,
,  . Then
. Then  satisfies the conditions of Theorem 4.6.
satisfies the conditions of Theorem 4.6.
References
Diening L: Maximal function on generalized Lebesgue spaces
 . Mathematical Inequalities & Applications 2004, 7(2):245–253.
. Mathematical Inequalities & Applications 2004, 7(2):245–253.Cruz-Uribe D, Fiorenza A, Neugebauer CJ: The maximal function on variable
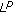 spaces. Annales Academiae Scientiarum Fennicae Mathematica 2003, 28(1):223–238.
spaces. Annales Academiae Scientiarum Fennicae Mathematica 2003, 28(1):223–238.Cruz-Uribe D, Fiorenza A, Neugebauer CJ: Erratum: The maximal function on variable
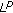 spaces. Annales Academiae Scientiarum Fennicae Mathematica 2004, 29(1):247–249.
spaces. Annales Academiae Scientiarum Fennicae Mathematica 2004, 29(1):247–249.Nekvinda A: Hardy-Littlewood maximal operator on
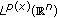 . Mathematical Inequalities & Applications 2004, 7(2):255–265.
. Mathematical Inequalities & Applications 2004, 7(2):255–265.Capone C, Cruz-Uribe D, Fiorenza A: The fractional maximal operator and fractional integrals on variable
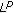 spaces. Revista Mathemática. Iberoamericana 2007, 23(3):743–770.
spaces. Revista Mathemática. Iberoamericana 2007, 23(3):743–770.Cruz-Uribe D, Fiorenza A, Martell JM, Pérez C: The boundedness of classical operators on variable
 spaces. Annales Academiæ Scientiarium Fennicæ. Mathematica 2006, 31(1):239–264.
spaces. Annales Academiæ Scientiarium Fennicæ. Mathematica 2006, 31(1):239–264.Harjulehto P, Hästö P, Latvala V: Sobolev embeddings in metric measure spaces with variable dimension. Mathematische Zeitschrift 2006, 254(3):591–609. 10.1007/s00209-006-0960-8
Harjulehto P, Hästö P, Pere M: Variable exponent Lebesgue spaces on metric spaces: the Hardy-Littlewood maximal operator. Real Analysis Exchange 2004/05, 30(1):87–103.
Kokilashvili V, Meskhi A: Maximal functions and potentials in variable exponent Morrey spaces with non-doubling measure. Complex Variables and Elliptic Equations 2010, 55(8–10):923–936.
Kokilashvili V, Samko S: The maximal operator in weighted variable spaces on metric measure spaces. Proceedings of A. Razmadze Mathematical Institute 2007, 144: 137–144.
Kokilashvili VM, Samko SG: Operators of harmonic analysis in weighted spaces with non-standard growth. Journal of Mathematical Analysis and Applications 2009, 352(1):15–34. 10.1016/j.jmaa.2008.06.056
Kokilashvili V, Samko S: The maximal operator in weighted variable exponent spaces on metric spaces. Georgian Mathematical Journal 2008, 15(4):683–712.
Khabazi M: Maximal functions in
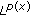 spaces. Proceedings of A. Razmadze Mathematical Institute 2004, 135: 145–146.
spaces. Proceedings of A. Razmadze Mathematical Institute 2004, 135: 145–146.Almeida A, Samko S: Fractional and hypersingular operators in variable exponent spaces on metric measure spaces. Mediterranean Journal of Mathematics 2009, 6(2):215–232. 10.1007/s00009-009-0006-7
Kokilashvili V, Samko S: Maximal and fractional operators in weighted
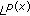 spaces. Revista Matemática Iberoamericana 2004, 20(2):493–515.
spaces. Revista Matemática Iberoamericana 2004, 20(2):493–515.Kokilashvili V, Samko S: On Sobolev theorem for Riesz-type potentials in Lebesgue spaces with variable exponent. Zeitschrift für Analysis und ihre Anwendungen 2003, 22(4):899–910.
Samko S, Vakulov B: Weighted Sobolev theorem with variable exponent for spatial and spherical potential operators. Journal of Mathematical Analysis and Applications 2005, 310(1):229–246. 10.1016/j.jmaa.2005.02.002
Samko NG, Samko SG, Vakulov BG: Weighted Sobolev theorem in Lebesgue spaces with variable exponent. Journal of Mathematical Analysis and Applications 2007, 335(1):560–583. 10.1016/j.jmaa.2007.01.091
Diening L, Samko S: Hardy inequality in variable exponent Lebesgue spaces. Fractional Calculus & Applied Analysis 2007, 10(1):1–18.
Edmunds DE, Kokilashvili V, Meskhi A: A trace inequality for generalized potentials in Lebesgue spaces with variable exponent. Journal of Function Spaces and Applications 2004, 2(1):55–69.
Edmunds DE, Kokilashvili V, Meskhi A: On the boundedness and compactness of weighted Hardy operators in spaces
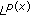 . Georgian Mathematical Journal 2005, 12(1):27–44.
. Georgian Mathematical Journal 2005, 12(1):27–44.Edmunds DE, Kokilashvili V, Meskhi A: Two-weight estimates in
 spaces with applications to Fourier series. Houston Journal of Mathematics 2009, 35(2):665–689.
spaces with applications to Fourier series. Houston Journal of Mathematics 2009, 35(2):665–689.Kokilashvili V, Meskhi A: Weighted criteria for generalized fractional maximal functions and potentials in Lebesgue spaces with variable exponent. Integral Transforms and Special Functions 2007, 18(9–10):609–628.
Kopaliani TS: On some structural properties of Banach function spaces and boundedness of certain integral operators. Czechoslovak Mathematical Journal 2004, 54(129)(3):791–805.
Diening L, Hästö P: Muckenhoupt weights in variable exponent spaces. preprint, http://www.helsinki.fi/~pharjule/varsob/publications.shtml
Kokilashvili V, Krbec M: Weighted inequalities in Lorentz and Orlicz spaces. World Scientific, River Edge, NJ, USA; 1991:xii+233.
Kokilashvili V: New aspects in the weight theory and applications. In Function Spaces, Differential Operators and Nonlinear Analysis (Paseky nad Jizerou, 1995). Edited by: Krbec Met al.. Prometheus, Prague, Czech Republic; 1996:51–70.
Strömberg J-O, Torchinsky A: Weighted Hardy Spaces, Lecture Notes in Mathematics. Volume 1381. Springer, Berlin, Germany; 1989:vi+193.
Coifman RR, Weiss G: Analyse Harmonique Non-Commutative sur Certains Espaces Homogènes, Lecture Notes in Mathematics. Volume 242. Springer, Berlin, Germany; 1971:v+160.
Folland GB, Stein EM: Hardy Spaces on Homogeneous Groups, Mathematical Notes. Volume 28. Princeton University Press, Princeton, NJ, USA; 1982:xii+285.
Edmunds DE, Kokilashvili V, Meskhi A: Bounded and Compact Integral Operators, Mathematics and Its Applications. Volume 543. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2002:xvi+643.
Kováčik O, Rákosník J: On spaces
 and
and  . Czechoslovak Mathematical Journal 1991, 41(116)(4):592–618.
. Czechoslovak Mathematical Journal 1991, 41(116)(4):592–618.Samko SG: Convolution type operators in
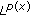 . Integral Transforms and Special Functions 1998, 7(1–2):123–144. 10.1080/10652469808819191
. Integral Transforms and Special Functions 1998, 7(1–2):123–144. 10.1080/10652469808819191Sharapudinov II: The topology of the space
 . Matematicheskie Zametki 1979, 26(4):613–632, 655.
. Matematicheskie Zametki 1979, 26(4):613–632, 655.Kokilashvili V, Meskhi A: Boundedness of maximal and singular operators in Morrey spaces with variable exponent. Armenian Journal of Mathematics 2008, 1(1):18–28.
Diening L: Riesz potential and Sobolev embeddings on generalized Lebesgue and Sobolev spaces
 and
and 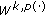 . Mathematische Nachrichten 2004, 268: 31–43. 10.1002/mana.200310157
. Mathematische Nachrichten 2004, 268: 31–43. 10.1002/mana.200310157Samko SG: Convolution and potential type operators in
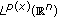 . Integral Transforms and Special Functions 1998, 7(3–4):261–284. 10.1080/10652469808819204
. Integral Transforms and Special Functions 1998, 7(3–4):261–284. 10.1080/10652469808819204
Acknowledgments
The first and second authors were partially supported by the Georgian National Science Foundation Grant (project numbers: GNSF/ST09/23/3-100 and GNSF/ST07/3-169). A part of this work was fulfilled in Abdus Salam School of Mathematical sciences, GC University, Lahore. The second and third authors are grateful to the Higher Educational Commission of Pakistan for financial support. The authors express their gratitude to the referees for their very useful remarks and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kokilashvili, V., Meskhi, A. & Sarwar, M. Potential Operators in Variable Exponent Lebesgue Spaces: Two-Weight Estimates. J Inequal Appl 2010, 329571 (2010). https://doi.org/10.1155/2010/329571
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/329571
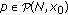 (resp.,
(resp., 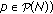 , then there are positive constants
, then there are positive constants 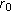 ,
, 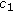 , and
, and 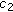 such that for all
such that for all  and all
and all 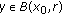 (resp., for all
(resp., for all  with
with 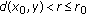 ), one has that
), one has that  .
.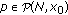 , then there are positive constants
, then there are positive constants  ,
, 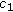 , and
, and  (in general, depending on
(in general, depending on  ) such that for all
) such that for all  (
(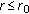 ) and all
) and all 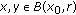 one has
one has 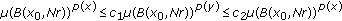 .
. , then there are positive constants
, then there are positive constants  ,
, 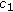 , and
, and  such that for all balls
such that for all balls 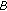 with radius
with radius  (
(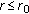 ) and all
) and all 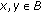 , one has that
, one has that 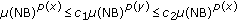 .
.

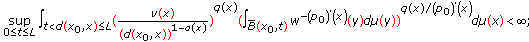
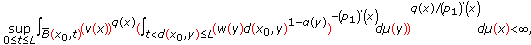
 . Mathematical Inequalities & Applications 2004, 7(2):245–253.
. Mathematical Inequalities & Applications 2004, 7(2):245–253. spaces. Annales Academiae Scientiarum Fennicae Mathematica 2003, 28(1):223–238.
spaces. Annales Academiae Scientiarum Fennicae Mathematica 2003, 28(1):223–238. spaces. Annales Academiae Scientiarum Fennicae Mathematica 2004, 29(1):247–249.
spaces. Annales Academiae Scientiarum Fennicae Mathematica 2004, 29(1):247–249.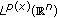 . Mathematical Inequalities & Applications 2004, 7(2):255–265.
. Mathematical Inequalities & Applications 2004, 7(2):255–265.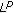 spaces. Revista Mathemática. Iberoamericana 2007, 23(3):743–770.
spaces. Revista Mathemática. Iberoamericana 2007, 23(3):743–770. spaces. Annales Academiæ Scientiarium Fennicæ. Mathematica 2006, 31(1):239–264.
spaces. Annales Academiæ Scientiarium Fennicæ. Mathematica 2006, 31(1):239–264.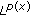 spaces. Proceedings of A. Razmadze Mathematical Institute 2004, 135: 145–146.
spaces. Proceedings of A. Razmadze Mathematical Institute 2004, 135: 145–146.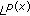 spaces. Revista Matemática Iberoamericana 2004, 20(2):493–515.
spaces. Revista Matemática Iberoamericana 2004, 20(2):493–515. . Georgian Mathematical Journal 2005, 12(1):27–44.
. Georgian Mathematical Journal 2005, 12(1):27–44. spaces with applications to Fourier series. Houston Journal of Mathematics 2009, 35(2):665–689.
spaces with applications to Fourier series. Houston Journal of Mathematics 2009, 35(2):665–689. and
and  . Czechoslovak Mathematical Journal 1991, 41(116)(4):592–618.
. Czechoslovak Mathematical Journal 1991, 41(116)(4):592–618. . Integral Transforms and Special Functions 1998, 7(1–2):123–144. 10.1080/10652469808819191
. Integral Transforms and Special Functions 1998, 7(1–2):123–144. 10.1080/10652469808819191 . Matematicheskie Zametki 1979, 26(4):613–632, 655.
. Matematicheskie Zametki 1979, 26(4):613–632, 655. and
and  . Mathematische Nachrichten 2004, 268: 31–43. 10.1002/mana.200310157
. Mathematische Nachrichten 2004, 268: 31–43. 10.1002/mana.200310157 . Integral Transforms and Special Functions 1998, 7(3–4):261–284. 10.1080/10652469808819204
. Integral Transforms and Special Functions 1998, 7(3–4):261–284. 10.1080/10652469808819204