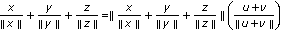- Research Article
- Open access
- Published:
On Sharp Triangle Inequalities in Banach Spaces II
Journal of Inequalities and Applications volume 2010, Article number: 323609 (2010)
Abstract
Sharp triangle inequality and its reverse in Banach spaces were recently showed by Mitani et al. (2007). In this paper, we present equality attainedness for these inequalities in strictly convex Banach spaces.
1. Introduction
In recent years, the triangle inequality and its reverse inequality have been treated in [1–5] (see also [6, 7]).Kato et al.[8] presented the following sharp triangle inequality and its reverse inequality with  elements in a Banach space
elements in a Banach space  .
.
Theorem 1.1 (see [8]).
For all nonzero elements  in a Banach space
in a Banach space  ,
,

These inequalities are useful to treat geometrical structure of Banach spaces, such as uniform non- -ness (see [8]). Moreover,Hsu et al.[9] presented these inequalities for strongly integrable functions with values in a Banach space.
-ness (see [8]). Moreover,Hsu et al.[9] presented these inequalities for strongly integrable functions with values in a Banach space.
Mitani et al.[10] showed the following inequalities which are sharper than Inequality (1.1) in Theorem 1.1.
Theorem 1.2 (see [10]).
For all nonzero elements  in a Banach space
in a Banach space  with
with  ,
,  ,
,


where  .
.
In this paper we first present a simpler proof of Theorem 1.2. To do this we consider the case  as follows.
as follows.
Theorem 1.3.
For all nonzero elements  in a Banach space
in a Banach space  with
with 


where  .
.
From this result we can easily obtain Theorem 1.2.
Moreover we consider equality attainedness for sharp triangle inequality and its reverse inequality in strictly convex Banach spaces. Namely, we characterize equality attainedness of Inequalities (1.4) and (1.5) in Theorem 1.3.
2. Simple Proofs of Theorems 1.2 and 1.3
Proof of Theorem 1.3.
According to Theorem 1.1 Inequalities (1.4) and (1.5) hold for the case  (cf. [3]). Therefore let
(cf. [3]). Therefore let  . We first prove (1.4) by the induction. Assume that (1.4) holds true for all
. We first prove (1.4) by the induction. Assume that (1.4) holds true for all  elements in
elements in  . Let
. Let  be any
be any  elements in
elements in  with
with  . Let
. Let

for all positive numbers  with
with  . Then
. Then

and  . By assumption,
. By assumption,

holds, where  . Since
. Since  , from (2.2) and (2.3),
, from (2.2) and (2.3),

and hence (1.4). Thus (1.4) holds true for all finite elements in  .
.
Next we show Inequality (1.5). Let

Then

and  Applying Inequality (1.4) to
Applying Inequality (1.4) to  ,
,

where  . Thus we obtain (1.5). This completes the proof.
. Thus we obtain (1.5). This completes the proof.
Proof of Theorem 1.2.
Let  be any nonzero elements in
be any nonzero elements in  with
with  . For all positive numbers
. For all positive numbers  with
with  let
let

Then  . Applying Theorem 1.3 to
. Applying Theorem 1.3 to  ,
,

where  for all positive numbers
for all positive numbers  with
with  . As
. As  , we have Inequalities (1.4) and (1.5).
, we have Inequalities (1.4) and (1.5).
3. Equality Attainedness in a Strictly Convex Banach Space
In this section we consider equality attainedness for sharp triangle inequality and its reverse inequality in a strictly convex Banach space. Kato et al. in [8] showed the following.
Theorem 3.1 (see [8]).
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  . Let
. Let  and
and  . Let
. Let  . Then
. Then

if and only if either
(a)
or
(b)
Theorem 3.2 (see [8]).
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  . Let
. Let  and
and  . Let
. Let  . Then
. Then

if and only if either
(a)
or
(b)
We present equality attainedness for (1.4) and (1.5) in Theorem 1.2. The following lemma given in [8] is quite powerful.
Lemma 3.3 (see [8]).
Let  be a strictly convex Banach space. Let
be a strictly convex Banach space. Let  be nonzero elements in
be nonzero elements in  . Then the following are equivalent.
. Then the following are equivalent.
(i) holds for any positive numbers
holds for any positive numbers  .
.
(ii) holds for some positive numbers
holds for some positive numbers  .
.
(iii) .
.
Theorem 3.4.
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  with
with  . Then
. Then

if and only if there exists a real number  with
with  satisfying
satisfying  .
.
Proof.
Assume that (3.3) is true. By Theorem 3.1, the equality (3.3) is equivalent to Equality

Put

Then  . Since
. Since  , we obtain
, we obtain  . Conversely, if
. Conversely, if  where
where  , then
, then

By  , we have (3.4). Thus we get (3.3).
, we have (3.4). Thus we get (3.3).
Next we consider the case  .
.
Theorem 3.5.
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  with
with  . Then
. Then

if and only if there exist  with
with  satisfying one of the following conditions:
satisfying one of the following conditions:
(a)
(b)
Proof.
Assume that (3.7) is true. Put

Then  and
and

Note that  . As in the proof of Theorem 1.2 given in [10], we have (3.7) if and only if we have the equalities
. As in the proof of Theorem 1.2 given in [10], we have (3.7) if and only if we have the equalities


By Theorem 3.4, Equality (3.11) implies that

for some  with
with  . By (3.8) we have
. By (3.8) we have

for some  . On the other hand, by Lemma 3.3, Equality (3.10) implies
. On the other hand, by Lemma 3.3, Equality (3.10) implies

Hence, by using (3.8), (3.12), and (3.13) we have  for some real number
for some real number  . Since
. Since  , we have
, we have  . We consider the following two cases
. We consider the following two cases
Case 1.

.
Equality (3.14) implies

Hence we have

By  and
and  , Equality (3.16) is valid for all real numbers
, Equality (3.16) is valid for all real numbers  with
with  .
.
Case 2.

.
Equality (3.14) implies

So we have

Hence  . Thus (
. Thus ( ) holds.
) holds.
Conversely, assume that there exist  with
with  satisfying one of the conditions
satisfying one of the conditions  and
and  . Then it is clear that (3.7) holds. Thus we obtain (
. Then it is clear that (3.7) holds. Thus we obtain ( ).
).
Moreover we consider general cases. For each  with
with  , we put
, we put  For
For  and
and  , we define
, we define

For a finite set  , the cardinal number of
, the cardinal number of  is denoted by
is denoted by  .
.
Lemma 3.6.
Let  . If
. If  for all
for all  with
with  , then
, then

Proof.
Let

where  and
and  . By the assumption, we have
. By the assumption, we have  . We first show
. We first show  for all
for all  with
with  . It is clear that
. It is clear that  . Assume that
. Assume that  for all
for all  with
with  . We will show
. We will show  . Suppose that
. Suppose that  . By
. By  , we have
, we have

Hence we have  which is a contradiction. Therefore we have
which is a contradiction. Therefore we have  . Namely,
. Namely,  for all
for all  with
with  . From this result, we obtain
. From this result, we obtain  . Hence
. Hence

Theorem 3.7.
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  with
with  . Then
. Then

if and only if there exists  with
with  such that
such that


for every  with
with  .
.
Proof.
( ): According to Theorems 3.4 and 3.5, Theorem 3.7 is valid for the cases
): According to Theorems 3.4 and 3.5, Theorem 3.7 is valid for the cases  . Therefore let
. Therefore let  . We will prove Theorem 3.7 by the induction. Assume that this theorem holds true for all nonzero elements in
. We will prove Theorem 3.7 by the induction. Assume that this theorem holds true for all nonzero elements in  less than
less than  . Let
. Let  and assume that Equality (3.24) holds. Let
and assume that Equality (3.24) holds. Let

for positive integer  with
with  . As in the proof of Theorem 1.3, Equality (3.24) holds if and only if
. As in the proof of Theorem 1.3, Equality (3.24) holds if and only if


hold, where  . Hence, by assumption, there exists
. Hence, by assumption, there exists  with
with  such that
such that

Since  by Lemma 3.6, we have
by Lemma 3.6, we have

Since

by the definition of  , we have
, we have

where

Since

we have

for all  with
with  . By Lemma 3.3, Equality (3.28) implies
. By Lemma 3.3, Equality (3.28) implies

Hence there exists  such that
such that  . Also,
. Also,


Since  , we have from (3.37) and (3.38),
, we have from (3.37) and (3.38),

which implies

If  , then it is clear that
, then it is clear that  .
.
If  , then, by (3.41), we have
, then, by (3.41), we have  . Hence
. Hence  . Thus we obtain
. Thus we obtain  .
.
( ): Let
): Let  with
with  satisfying (3.25) and (3.26), and let
satisfying (3.25) and (3.26), and let  . From (3.25) we have
. From (3.25) we have

By Lemma 3.6,

Let  , where
, where  . From (3.26) and
. From (3.26) and  we have
we have

Thus we obtain (3.24). This completes the proof.
In what follows, we characterize the equality condition of Inequality (1.3) in Theorem 1.2. For  and positive integer
and positive integer  with
with  we define
we define 
 , and
, and 
Lemma 3.8.
Let  with
with  . If
. If

for all positive integers  with
with  , then one has
, then one has

Proof.
Let  and
and  , where
, where  and
and  . As in the proof of Lemma 3.6, we have
. As in the proof of Lemma 3.6, we have  for all
for all  . So
. So  for all
for all  . Hence
. Hence

This completes the proof.
Theorem 3.9.
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  with
with  . Then
. Then

holds if and only if there exists  with
with  ,
,  for all positive integers
for all positive integers  with
with  satisfying
satisfying

for all positive integers  with
with  and
and  .
.
Proof.

: Let  and
and

For positive integers  with
with  we put
we put

Note that  and
and

Then Equality (3.48) holds if and only if


Thus, by the equality condition of sharp triangle inequality with  elements, there exists
elements, there exists  such that
such that

for all positive integers  with
with  ,
,

for all positive integers  with
with  . Since
. Since

for each  with
with  , we have
, we have  , where
, where

Note that  and
and  . By (3.53),
. By (3.53),

Hence there exists  such that
such that  . We also have
. We also have  and
and

Hence we have

From (3.3), we obtain  . Thus we have (
. Thus we have ( ).
).
( ): Assume that there exists
): Assume that there exists  with
with  ,
,  for all positive integers
for all positive integers  with
with  satisfying (3.49) for all positive integers
satisfying (3.49) for all positive integers  with
with  and
and  . By Theorem 3.7, we have (3.54). From the assumption,
. By Theorem 3.7, we have (3.54). From the assumption,

By  and Lemma 3.8, we obtain (3.53). Thus we have (
and Lemma 3.8, we obtain (3.53). Thus we have ( ). This completes the proof.
). This completes the proof.
If  , then we have the following corollary.
, then we have the following corollary.
Corollary 3.10.
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  with
with  . Then
. Then

if and only if there exists a real number  with
with  such that
such that  .
.
If  , then we have the following corollary.
, then we have the following corollary.
Corollary 3.11.
Let  be a strictly convex Banach space and
be a strictly convex Banach space and  nonzero elements in
nonzero elements in  with
with  . Then
. Then

if and only if there exist  with
with  such that
such that  and
and  .
.
4. Remark
In this section we consider equality attainedness for sharp triangle inequality in a more general case, that is, the case without the assumption that  . Let us consider the case
. Let us consider the case  .
.
Proposition 4.1.
Let  be a strictly convex Banach space, and
be a strictly convex Banach space, and  nonzero elements in
nonzero elements in  .
.
(i)If  , then the equality
, then the equality

always holds.
(ii)If  , then the equality (4.1) holds if and only if there exists a real number
, then the equality (4.1) holds if and only if there exists a real number  satisfying
satisfying  and
and  .
.
(iii)If  , then the equality (4.1) holds if and only if there exists a real number
, then the equality (4.1) holds if and only if there exists a real number  satisfying
satisfying  and
and  .
.
Proof.
-
(i)
Is clear.
-
(ii)
Assume that (4.1) holds. By
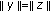 , (4.1) implies
, (4.1) implies 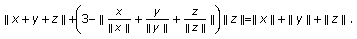 (4.2)
(4.2)
From Theorem 3.1, we have

Hence  for some
for some  . The following
. The following

implies

Hence  and so
and so  The converse is clear.
The converse is clear.
-
(iii)
Assume that (4.1) holds. Put
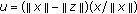 and
and  . As in the proof of Theorem 3.5, we have
. As in the proof of Theorem 3.5, we have 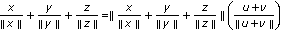 (4.6)
(4.6)
Since  , we have
, we have  for some
for some  . The following
. The following

implies

Hence  . The converse is clear.
. The converse is clear.
Conjecture 1.
What is the necessary and sufficient condition when Equality (3.24) (resp. Equality (3.48)) holds for  elements
elements  with
with  in Theorem 3.7 (resp. Theorem 3.9)?
in Theorem 3.7 (resp. Theorem 3.9)?
References
Diaz JB, Metcalf FT: A complementary triangle inequality in Hilbert and Banach spaces. Proceedings of the American Mathematical Society 1966, 17: 88–97. 10.1090/S0002-9939-1966-0188748-8
Dragomir SS: Reverses of the triangle inequality in Banach spaces. Journal of Inequalities in Pure and Applied Mathematics 2005, 6(5, article 129):1–46.
Hudzik H, Landes TR: Characteristic of convexity of Köthe function spaces. Mathematische Annalen 1992, 294(1):117–124. 10.1007/BF01934317
Mitrinović DS, Pečarić JE, Fink AM: Classical and New Inequalities in Analysis, Mathematics and Its Applications (East European Series). Volume 61. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xviii+740.
Pečarić J, Rajić R: The Dunkl-Williams inequality with elements in normed linear spaces. Mathematical Inequalities & Applications 2007, 10(2):461–470.
Dunkl CF, Williams KS: A simple norm inequality. The American Mathematical Monthly 1964, 71(1):53–54. 10.2307/2311304
Massera JL, Schäffer JJ: Linear differential equations and functional analysis. I. Annals of Mathematics 1958, 67: 517–573. 10.2307/1969871
Kato M, Saito K-S, Tamura T: Sharp triangle inequality and its reverse in Banach spaces. Mathematical Inequalities & Applications 2007, 10(2):451–460.
Hsu C-Y, Shaw S-Y, Wong H-J: Refinements of generalized triangle inequalities. Journal of Mathematical Analysis and Applications 2008, 344(1):17–31. 10.1016/j.jmaa.2008.01.088
Mitani K-I, Saito K-S, Kato M, Tamura T: On sharp triangle inequalities in Banach spaces. Journal of Mathematical Analysis and Applications 2007, 336(2):1178–1186. 10.1016/j.jmaa.2007.03.036
Acknowledgment
The second author was supported in part by Grants-in-Aid for Scientific Research (no. 20540158), Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mitani, KI., Saito, KS. On Sharp Triangle Inequalities in Banach Spaces II. J Inequal Appl 2010, 323609 (2010). https://doi.org/10.1155/2010/323609
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/323609
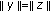 , (4.1) implies
, (4.1) implies 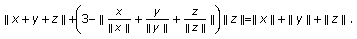
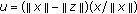 and
and  . As in the proof of Theorem 3.5, we have
. As in the proof of Theorem 3.5, we have