- Research Article
- Open access
- Published:
Some Comparison Inequalities for Generalized Muirhead and Identric Means
Journal of Inequalities and Applications volume 2010, Article number: 295620 (2010)
Abstract
For  , with
, with  , the generalized Muirhead mean
, the generalized Muirhead mean  with parameters
with parameters  and
and  and the identric mean
and the identric mean  are defined by
are defined by  and
and  ,
,  ,
,  ,
,  , respectively. In this paper, the following results are established: (1)
, respectively. In this paper, the following results are established: (1)  for all
for all  with
with  and
and  ; (2)
; (2)  for all
for all  with
with  and
and  ; (3) if
; (3) if  , then there exist
, then there exist  such that
such that  and
and  .
.
1. Introduction
For  ,
,  , with
, with  , the generalized Muirhead mean
, the generalized Muirhead mean  with parameters
with parameters  and
and  and the identric mean
and the identric mean  are defined by
are defined by


respectively.
The generalized Muirhead mean was introduced by Trif [1], the monotonicity of  with respect to
with respect to  or
or  was discussed, and a comparison theorem and a Minkowski-type inequality involving the generalized Muirhead mean
was discussed, and a comparison theorem and a Minkowski-type inequality involving the generalized Muirhead mean  were discussed.
were discussed.
It is easy to see that the generalized Muirhead mean  is continuous on the domain
is continuous on the domain  and differentiable with respect to
and differentiable with respect to  for fixed
for fixed  with
with  . It is symmetric in
. It is symmetric in  and
and  and in
and in  and
and  . Many means are special cases of the generalized Muirhead mean, for example,
. Many means are special cases of the generalized Muirhead mean, for example,

The well-known Muirhead inequality [2] implies that if  are fixed, then
are fixed, then  is Schur convex on the domain
is Schur convex on the domain  and Schur concave on the domain
and Schur concave on the domain  . Chu and Xia [3] discussed the Schur convexity and Schur concavity of
. Chu and Xia [3] discussed the Schur convexity and Schur concavity of  with respect to
with respect to  for fixed
for fixed  with
with  .
.
Recently, the identric mean  has been the subject of intensive research. In particular, many remarkable inequalities for the identric mean
has been the subject of intensive research. In particular, many remarkable inequalities for the identric mean  can be found in the literature [4–13].
can be found in the literature [4–13].
The power mean of order  of the positive real numbers
of the positive real numbers  and
and  is defined by
is defined by

The main properties of the power mean  are given in [14]. In particular,
are given in [14]. In particular,  is continuous and increasing with respect to
is continuous and increasing with respect to  for fixed
for fixed  . Let
. Let  ,
,


and  be the arithmetic, logarithmic, geometric, and harmonic means of two positive numbers
be the arithmetic, logarithmic, geometric, and harmonic means of two positive numbers  and
and  . Then it is well known that
. Then it is well known that

for all  with
with  .
.
The following sharp inequality is due to Carlson [15]:

for all  with
with  .
.
Pittenger [16] proved that

for all  with
with  , and
, and  and
and  are the optimal upper and lower power mean bounds for the identric mean
are the optimal upper and lower power mean bounds for the identric mean  .
.
In [8, 9], Sándor established that

for all  with
with  .
.
Alzer and Qiu [5] proved the inequalities

for all  with
with  if and only if
if and only if  and
and  .
.
In [3], Chu and Xia proved that

for all  and
and  , and
, and

for all  and
and  .
.
Our purpose in what follows is to compare the generalized Muirhead mean  with the identric mean
with the identric mean  . Our main result is Theorem 1.1 which follows.
. Our main result is Theorem 1.1 which follows.
Theorem.
Suppose that  ,
,  and
and  . The following statements hold,
. The following statements hold,
() If  , then
, then  for all
for all  with
with 
() If  , then
, then  for all
for all  with
with 
() If  , then there exist
, then there exist  such that
such that  and
and  .
.
2. Lemma
In order to prove Theorem 1.1 we need Lemma 2.1 that follows.
Lemma.
Let  and
and  be two real numbers such that
be two real numbers such that  and
and  . Let one define the function
. Let one define the function  as follows:
as follows:

then the following statements hold.
(1)If  and
and  , then
, then  for
for 
-
(2)
If
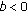 ,
, 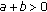 ,
, 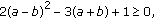 and
and 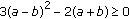 , then
, then  for
for 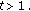
(3) If  , then
, then  for
for  .
.
Proof.
Simple computations lead to




where





where



( ) We divide the proof of Lemma 2.1(
) We divide the proof of Lemma 2.1( ) into two cases.
) into two cases.
Case.

,  and
and  . From (2.13), (2.12), (2.9), and (2.4), we clearly see that
. From (2.13), (2.12), (2.9), and (2.4), we clearly see that

Therefore,  for
for  easily follows from (2.2), (2.5), (2.7), (2.10), and (2.14).
easily follows from (2.2), (2.5), (2.7), (2.10), and (2.14).
Case 2.

,  and
and  we conclude that
we conclude that

In fact, we clearly see that  for
for  , and
, and  for
for  and
and  .
.
Equation (2.15) and  imply that
imply that

Therefore,  for
for  follows from (2.16) together with that
follows from (2.16) together with that  can be rewritten as
can be rewritten as

( ) If
) If  ,
,  ,
,  and
and  , then from (2.13), (2.12), (2.9), and (2.4) we get
, then from (2.13), (2.12), (2.9), and (2.4) we get

Therefore,  for
for  easily follows from (2.2), (2.5), (2.7), and (2.10) together with (2.18).
easily follows from (2.2), (2.5), (2.7), and (2.10) together with (2.18).
-
(3)
If
 , then we clearly see that inequalities (2.14) again hold, and
, then we clearly see that inequalities (2.14) again hold, and 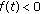 for
for 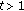 follows from (2.2), (2.5), (2.7), and (2.10) together with (2.14).
follows from (2.2), (2.5), (2.7), and (2.10) together with (2.14).
3. Proof of Theorem 1.1
Proof of Theorem 1.1.
For convenience, we introduce the following classified regions in  :
:

Then we clearly see that  ,
,  and
and  .
.
Without loss of generality, we assume that  . From the symmetry we clearly see that Theorem 1.1 is true if we prove that
. From the symmetry we clearly see that Theorem 1.1 is true if we prove that  is positive, negative, and neither positive nor negative with respect to
is positive, negative, and neither positive nor negative with respect to  for
for  ,
,  and
and  .
.
Let  , then (1.1) and (1.2) lead to
, then (1.1) and (1.2) lead to

Let

Then simple computations yield

where

Note that


where  is defined as in Lemma 2.1.
is defined as in Lemma 2.1.
We divide the proof into three cases.
Case.

. We divide our discussion into two subcases.
Subcase 1.

. From Lemma 2.1(2) we get

for  .
.
Equations (3.3)–(3.8) imply that

for  .
.
Therefore,  follows from (3.2) and (3.9).
follows from (3.2) and (3.9).
Subcase 2.

. Then from (1.1), (1.4), and (1.6) together with the monotonicity of the power mean  with respect to
with respect to  for fixed
for fixed  , we get
, we get

Case.

. We divide our discussion into four subcases.
Subcase 3.

. Then Lemma 2.1(1) leads to

for  .
.
Therefore,  follows from (3.2)–(3.7) and (3.11).
follows from (3.2)–(3.7) and (3.11).
Subcase 4.

. Then from (1.1), (1.4), and (1.8) together with the monotonicity of the power mean  with respect to
with respect to  for fixed
for fixed  we clearly see that
we clearly see that

Subcase 5.

. Then from Lemma 2.1(3) we know that (3.11) holds again; hence,  .
.
Subcase 6.

. Then (1.6) leads to

Case.

. We divide our discussion into two subcases.
Subcase 7.

. Then (2.4) leads to

Inequality (3.14) and the continuity of  imply that there exists
imply that there exists  such that
such that

for  .
.
From (2.2) and (3.15) we clearly see that

for  .
.
Therefore,  for
for  follows from (3.2)–(3.7) and (3.16).
follows from (3.2)–(3.7) and (3.16).
On the other hand, from (3.3) we clearly see that

Equations (3.2) and (3.3) together with (3.17) imply that there exists sufficient large  such that
such that  for
for  .
.
Subcase 8.

. Then (2.2) and (2.4) together with the continuity of  imply that there exists
imply that there exists  such that
such that

for  .
.
Therefore,  for
for  follows from (3.2)–(3.7) and (3.18).
follows from (3.2)–(3.7) and (3.18).
On the other hand, from (3.3) we clearly see that

Equations (3.2) and (3.3) together with (3.19) imply that there exists sufficient large  such that
such that  for
for  .
.
Remark.
Let  , then
, then  . Unfortunately, in this paper we cannot discuss the case of
. Unfortunately, in this paper we cannot discuss the case of  we leave it as an open problem to the readers.
we leave it as an open problem to the readers.
References
Trif T: Monotonicity, comparison and Minkowski's inequality for generalized Muirhead means in two variables. Mathematica 2006, 48(71)(1):99–110.
Hardy GH, Littlewood JE, Pólya G: Inequalties. Cambridge University Press, Cambridge, UK; 1934.
Chu Y-M, Xia W-F: The Schur convexity for the generalized Muirhead mean. to appear in Bulletin mathématique de la Société des Sciences Mathématiques de Roumanie to appear in Bulletin mathématique de la Société des Sciences Mathématiques de Roumanie
Qi F, Guo B-N: An inequality between ratio of the extended logarithmic means and ratio of the exponential means. Taiwanese Journal of Mathematics 2003, 7(2):229–237.
Alzer H, Qiu S-L: Inequalities for means in two variables. Archiv der Mathematik 2003, 80(2):201–215. 10.1007/s00013-003-0456-2
Alzer H: Ungleichungen für Mittelwerte. Archiv der Mathematik 1986, 47(5):422–426. 10.1007/BF01189983
Sándor J: Inequalities for means. In Proceedings of the 3rd Symposium of Mathematics and Its Applications (Timişoara, 1989), Timişoara, Romania. Romanian Academy; 87–90, 1990.
Sándor J: On the identric and logarithmic means. Aequationes Mathematicae 1990, 40(2–3):261–270.
Sándor J: A note on some inequalities for means. Archiv der Mathematik 1991, 56(5):471–473. 10.1007/BF01200091
Sándor J: On certain identities for means. Universitatis Babeş-Bolyai. Studia. Mathematica 1993, 38(4):7–14.
Sándor J: On refinements of certain inequalities for means. Archivum Mathematicum 1995, 31(4):279–282.
Sándor J: Two inequalities for means. International Journal of Mathematics and Mathematical Sciences 1995, 18(3):621–623. 10.1155/S0161171295000792
Sándor J, Raşa I: Inequalities for certain means in two arguments. Nieuw Archief voor Wiskunde. Vierde Serie 1997, 15(1–2):51–55.
Bullen PS, Mitrinović DS, Vasić PM: Means and Their Inequalities, Mathematics and Its Applications (East European Series). Volume 31. D. Reidel, Dordrecht, The Netherlands; 1988:xx+459.
Carlson BC: The logarithmic mean. The American Mathematical Monthly 1972, 79: 615–618. 10.2307/2317088
Pittenger AO: Inequalities between arithmetic and logarithmic means. Publikacije Elektrotehničkog Fakulteta. Serija Matematika i Fizika 1981, 1980(678–715):15–18.
Acknowledgments
This research is partly supported by N. S. Foundation of China under grant no. 60850005 and the N. S. Foundation of Zhejiang Province under grants no. D7080080 and no. Y607128.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, MK., Chu, YM. & Qiu, YF. Some Comparison Inequalities for Generalized Muirhead and Identric Means. J Inequal Appl 2010, 295620 (2010). https://doi.org/10.1155/2010/295620
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/295620
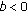 ,
, 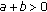 ,
, 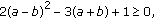 and
and 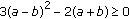 , then
, then  for
for 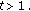
 , then we clearly see that inequalities (2.14) again hold, and
, then we clearly see that inequalities (2.14) again hold, and 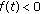 for
for 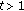 follows from (2.2), (2.5), (2.7), and (2.10) together with (2.14).
follows from (2.2), (2.5), (2.7), and (2.10) together with (2.14).