- Research Article
- Open access
- Published:
Global Existence, Uniqueness, and Asymptotic Behavior of Solution for 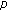 -Laplacian Type Wave Equation
-Laplacian Type Wave Equation
Journal of Inequalities and Applications volume 2010, Article number: 216760 (2010)
Abstract
We study the global existence and uniqueness of a solution to an initial boundary value problem for the nonlinear wave equation with the  -Laplacian operator
-Laplacian operator  . Further, the asymptotic behavior of solution is established. The nonlinear term
. Further, the asymptotic behavior of solution is established. The nonlinear term  likes
likes  with appropriate functions
with appropriate functions  and
and  , where
, where  .
.
1. Introduction
This paper is concerned with the global existence, uniqueness, and asymptotic behavior of solution for the nonlinear wave equation with the  -Laplacian operator
-Laplacian operator


where  and
and  is a boundary domain in
is a boundary domain in  with smooth boundary
with smooth boundary  . The assumptions on
. The assumptions on  and
and  will be made in the sequel.
will be made in the sequel.
Recently, Ma and Soriano in [1] investigated the global existence of solution  for the problem (1.1)-(1.2) under the assumptions
for the problem (1.1)-(1.2) under the assumptions

Moreover, if  and
and  then there exist positive constants
then there exist positive constants  and
and  such that
such that


where

with 
Gao and Ma in [2] also considered the global existence of solution for (1.1)-(1.2). In Theorem  of [2], the similar results to (1.4)-(1.5) for asymptotic behavior of solution were obtained if the nonlinear function
of [2], the similar results to (1.4)-(1.5) for asymptotic behavior of solution were obtained if the nonlinear function  satisfies
satisfies

where  if
if  and
and  if
if  .
.
More precisely, they obtained that the global existence of solution for (1.1)-(1.2) if one of the following assumptions was satisfied:
(i) , the initial data
, the initial data  ;
;
(ii) , the initial data
, the initial data  is small.
is small.
Similar consideration can be found in [3–5]. In [6], Yang obtained the uniqueness of solution of the Laplacian wave equation (1.1)-(1.2) for  . To the best of our knowledge, there are few information on the uniqueness of solution of (1.1)-(1.2) for
. To the best of our knowledge, there are few information on the uniqueness of solution of (1.1)-(1.2) for  and
and  .
.
In this paper, we are interested in the global existence, the uniqueness, the continuity and the asymptotic behavior of solution for (1.1)-(1.2). The nonlinear term  in (1.1) likes
in (1.1) likes  with
with  and
and  . Obviously, the sign condition
. Obviously, the sign condition  fails to hold for this type of function.
fails to hold for this type of function.
For these purposes, we must establish the global existence of solution for (1.1)-(1.2). Several methods have been used to study the existence of solutions to nonlinear wave equation. Notable among them is the variational approach through the use of Faedo-Galerkin approximation combined with the method of compactness and monotonicity, see [7]. To prove the uniqueness, we need to derive the various estimates for assumed solution  . For the decay property, like (1.5), we use the method recently introduced by Martinez [8] to study the decay rate of solution to the wave equation
. For the decay property, like (1.5), we use the method recently introduced by Martinez [8] to study the decay rate of solution to the wave equation  in
in  , where
, where  is a bounded domain of
is a bounded domain of  .
.
This paper is organized as follows. In Section 2, some assumptions and the main results are stated. In Section 3, we use Faedo-Galerkin approximation together with a combination of the compactness and the monotonicity methods to prove the global existence of solution to problem (1.1)-(1.2). Further, we establish the uniqueness of solution by some a priori estimate to assumed solutions. The proof of asymptotic behavior of solution is given in Section 4.
2. Assumptions and Main Results
We first give some notations and definitions. Let  be a bounded domain in
be a bounded domain in  with smooth boundary
with smooth boundary  . We denote the space
. We denote the space  and
and  for
for  and
and  and relevant norms by
and relevant norms by  and
and  , respectively. In general,
, respectively. In general,  denotes the norm of Banach space
denotes the norm of Banach space  . We also denote by
. We also denote by  and
and  the inner product of
the inner product of  and the duality pairing between
and the duality pairing between  and
and  , respectively. As usual, we write
, respectively. As usual, we write  instead
instead  . Sometimes, let
. Sometimes, let  represent for
represent for  and so on.
and so on.
If  is given and
is given and  is a Banach space, we denote by
is a Banach space, we denote by  the space of functions which are
the space of functions which are  over
over  and which take their values in
and which take their values in  . In this space, we consider the norm
. In this space, we consider the norm

Let us state our assumptions on  and
and  .
.
() with
with  .
.
()Let  and satisfy
and satisfy

and growth condition

with some  and the nonnegative functions
and the nonnegative functions  ,
,  ,
,  , where
, where  ,
,  .
.
A typical function  is
is  with the appropriate nonnegative functions
with the appropriate nonnegative functions  and
and  , where
, where  .
.
Definition 2.1 (see [7]).
A measurable function  on
on  is said to be a (weak) solution of (1.1)-(1.2) if all
is said to be a (weak) solution of (1.1)-(1.2) if all  ,
,  ,
,  ,
,  , and
, and  satisfies (1.2) with
satisfies (1.2) with  and the integral identity
and the integral identity

for all  .
.
Now we are in a position to state our results.
Theorem 2.2.
Assume  -
- hold and
hold and  . Then the problem (1.1)-(1.2) admits a solution
. Then the problem (1.1)-(1.2) admits a solution  satisfying
satisfying

and the following estimates

where

with 
 .
.

Further, if  and
and  , the solution satisfying (2.5)-(2.6) is unique.
, the solution satisfying (2.5)-(2.6) is unique.
Theorem 2.3.
Let  be a solution of (1.1)-(1.2) with
be a solution of (1.1)-(1.2) with  . In addition, let
. In addition, let  and
and

Then there exists  , such that
, such that

The following theorem shows that the asymptotic estimate (2.9) can be also derived if assumption (2.8) fails to hold.
Theorem 2.4.
Let  be a solution of (1.1)-(1.2) with
be a solution of (1.1)-(1.2) with  . In addition, let
. In addition, let  and
and

with  . Then there exists
. Then there exists  and
and  , such that
, such that  the solution
the solution  satisfies
satisfies

3. Proof of Theorem 2.2
In this section, we assume that all assumptions in Theorem 2.2 are satisfied. We first prove the global existence of a solution to problem (1.1)-(1.2) with the Faedo-Galerkin method as in [1, 2, 7, 9].
Let  be an integer for which the embedding
be an integer for which the embedding  is continuous. Let
is continuous. Let  be eigenfunctions of the spectral problem
be eigenfunctions of the spectral problem

where  represents the inner product in
represents the inner product in  . Then the family
. Then the family  yields a basis for both
yields a basis for both  and
and  . For each integer
. For each integer  , let
, let  span
span . We look for an approximate solution to problem (1.1)-(1.2) in the form
. We look for an approximate solution to problem (1.1)-(1.2) in the form

where  are the solution of the nonlinear ODE system in the variant
are the solution of the nonlinear ODE system in the variant  :
:

with the  -Laplacian operator
-Laplacian operator  and the initial conditions
and the initial conditions

where  and
and  are chosen in
are chosen in  so that
so that

As it is well known, the system (3.3)-(3.4) has a local solution  on some interval
on some interval  We claim that for any
We claim that for any  , such a solution can be extended to the whole interval
, such a solution can be extended to the whole interval  by using the first a priori estimate below. We denote by
by using the first a priori estimate below. We denote by  the constant which is independent of
the constant which is independent of  and the initial data
and the initial data  and
and  .
.
Multiplying (3.3) by  and summing the resulting equations over
and summing the resulting equations over  , we get after integration by parts
, we get after integration by parts

where

By (2.2) and Young inequality, we have

Let  be so small that
be so small that  . Then
. Then

or

for some  .
.
Thus, it follows from (3.6) and (3.10) that, for any  and
and 

By assumption  , we obtain that
, we obtain that  and
and

Then it follows (3.5) and (3.6) that

Hence, for any  and
and  , we have from (3.11) and (3.13) that
, we have from (3.11) and (3.13) that

With this estimate we can extend the approximate solution  to the interval
to the interval  and we have that
and we have that



Now we recall that operator  is bounded, monotone, and hemicontinuous from
is bounded, monotone, and hemicontinuous from  to
to  with
with  . Then we have
. Then we have

By the standard projection argument as in [1], we can get from the approximate equation (3.3) and the estimates (3.15)–(3.17) that

From (3.15)-(3.16), going to a subsequence if necessary, there exists  such that
such that



and in view of (3.18), there exists  such that
such that

By applying the Lions-Aubin compactness Lemma in [7], we get, from (3.15) and (3.16),

and  a.e. in
a.e. in  .
.
Since the embedding  is compact, we get, from (3.18) and (3.19),
is compact, we get, from (3.18) and (3.19),

Using the growth condition (2.3) and (3.25), we see that

is bounded and

Therefore, from [7, Chapter  , Lemma
, Lemma  ], we infer that
], we infer that

With these convergences, we can pass to the limit in the approximate equation and then

Obviously,  satisfies the estimates (2.5)-(2.6). Finally, using the standard monotonicity argument as done in [1, 7], we get that
satisfies the estimates (2.5)-(2.6). Finally, using the standard monotonicity argument as done in [1, 7], we get that  . This completes the proof of existence of solution
. This completes the proof of existence of solution  .
.
To prove the uniqueness, we assume that  and
and  are two solutions which satisfy (2.5)-(2.6) and
are two solutions which satisfy (2.5)-(2.6) and  . Setting
. Setting  , and
, and  . We see from (1.1) and (1.2) that
. We see from (1.1) and (1.2) that

Multiplying (3.30) by  and integrating over
and integrating over  , we have
, we have

Now setting  , then
, then

Note that

Then, by the estimates (2.6) and  , we have
, we have

with  .
.
For the term of the right side to (3.31), we have

with  ,
,  .
.
By the assumption  and
and  , we see that
, we see that

By the estimate (2.6), we have

Therefore, there exists  , depending
, depending 
 such that
such that

Since  ,
,  , we get
, we get

Then (3.35) becomes

Therefore, it follows from (3.31), (3.34), and (3.40) that

The integral inequality (3.41) shows that there exists  , such that
, such that

Consequently,  .
.
Repeating the above procedure, we conduce that  on
on  and
and  on
on  . This ends the proof of uniqueness.
. This ends the proof of uniqueness.
Next, we prove that  . Let
. Let  , we have
, we have

This shows that  . We complete the proof of Theorem 2.2.
. We complete the proof of Theorem 2.2.
4. Proof of Theorem 2.3
Let us first state a well-known lemma that will be needed later.
Lemma 4.1 (see [10]).
Let  be a nonincreasing function and assume that there are constants
be a nonincreasing function and assume that there are constants  and
and  , such that
, such that

Then, we have

4.1. The Proof of Theorem 2.3
Let

Then, we have from (1.1) that

This shows that  is nonincreasing in
is nonincreasing in  .
.
Multiplying (1.1) by  with
with  , we get
, we get

Note that

Then we havefrom (4.5) that

Since  ,
,  . Further, by (4.4), we see that
. Further, by (4.4), we see that

with  .
.
This gives

where the fact that  is nonincreasing is used.
is nonincreasing is used.
Similarly, we derive the following estimates



Then we get from (4.9)–(4.12) that

for any  , letting
, letting  , we find that
, we find that

By Lemma 4.1, we obtain that

This is (2.9) and we complete the proof of Theorem 2.3.
4.2. The Proof of Theorem 2.4
By Sobolev inequality, we know that there exists  such that
such that

Let  be a solution for (1.1)-(1.2) in Theorem 2.2. By (2.10),
be a solution for (1.1)-(1.2) in Theorem 2.2. By (2.10),

Obviously, there exists  , such that
, such that  ,
,

This implies that

On the other hand, we have, from (4.18) and (4.19),

It shows that

Then, by (4.9) and (4.11)–(4.14), we have

The applications of Lemma 4.1 and (4.19) yields that

This ends the proof of Theorem 2.4.
References
Ma TF, Soriano JA: On weak solutions for an evolution equation with exponential nonlinearities. Nonlinear Analysis: Theory, Methods & Applications 1999, 37(8):1029–1038. 10.1016/S0362-546X(97)00714-1
Gao H, Ma TF: Global solutions for a nonlinear wave equation with the -Laplacian operator. Electronic Journal of Qualitative Theory of Differential Equations 1999, (11):1–13.
Benaissa A, Guesmia A: Energy decay for wave equations of -Laplacian type with weakly nonlinear dissipation. Electronic Journal of Differential Equations 2008, 2008(109):1–22.
Biazutti AC: On a nonlinear evolution equation and its applications. Nonlinear Analysis: Theory, Methods & Applications 1995, 24(8):1221–1234. 10.1016/0362-546X(94)00193-L
Nakao M, Yang ZJ: Global attractors for some quasi-linear wave equations with a strong dissipation. Advances in Mathematical Sciences and Applications 2007, 17(1):89–105.
Yang ZJ: Existence and asymptotic behaviour of solutions for a class of quasi-linear evolution equations with non-linear damping and source terms. Mathematical Methods in the Applied Sciences 2002, 25(10):795–814. 10.1002/mma.306
Lions J-L: Quelques Méthodes de Résolution des Problèmes aux Limites non Linéaires. Dunod-Gauthier Villars, Paris, France; 1969:xx+554.
Martinez P: A new method to obtain decay rate estimates for dissipative systems. ESAIM: Control, Optimisation and Calculus of Variations 1999, 4: 419–444.
Sango M: On a nonlinear hyperbolic equation with anisotropy: global existence and decay of solution. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(7):2816–2823. 10.1016/j.na.2008.04.006
Komornik V: Exact Controllability and Stabilization: The Multiplier Method, RAM: Research in Applied Mathematics. John Wiley & Sons, Chichester, UK; Masson, Paris, France; 1994:viii+156.
Acknowledgments
The authors express their sincere gratitude to the anonymous referees for a number of valuable comments and suggestions. The work was supported by the Science Funds of Hohai University (Grant Nos. 2008430211 and 2008408306) and the Fundamental Research Funds for the Central Universities (Grant No. 2010B17914).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, C., Yao, H. & Shao, L. Global Existence, Uniqueness, and Asymptotic Behavior of Solution for 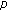 -Laplacian Type Wave Equation.
J Inequal Appl 2010, 216760 (2010). https://doi.org/10.1155/2010/216760
-Laplacian Type Wave Equation.
J Inequal Appl 2010, 216760 (2010). https://doi.org/10.1155/2010/216760
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/216760