- Research Article
- Open access
- Published:
A T-S Fuzzy Model-Based Adaptive Exponential Synchronization Method for Uncertain Delayed Chaotic Systems: An LMI Approach
Journal of Inequalities and Applications volume 2010, Article number: 168962 (2010)
Abstract
This paper proposes a new fuzzy adaptive exponential synchronization controller for uncertain time-delayed chaotic systems based on Takagi-Sugeno (T-S) fuzzy model. This synchronization controller is designed based on Lyapunov-Krasovskii stability theory, linear matrix inequality (LMI), and Jesen's inequality. An analytic expression of the controller with its adaptive laws of parameters is shown. The proposed controller can be obtained by solving the LMI problem. A numerical example for time-delayed Lorenz system is presented to demonstrate the validity of the proposed method.
1. Introduction
Chaos synchronization is an important subject both theoretically and practically, for applications requiring oscillations out of chaos, machine and building structural stability analysis, chaos generators design and so on. Chaos synchronization, first described by Fujisaka and Yamada [1] in 1983, did not received great attention until 1990 [2]. From then on, chaos synchronization has been developed extensively due to its various applications [3]. During the last decade, several techniques for handling chaos synchronization have been developed, such as variable structure control [4], OGY method [5], observer-based control [6], active control [7], backstepping design technique [8],  approach [9], and passivity based method [10].
approach [9], and passivity based method [10].
Time delay inevitably appears in many physical systems such as aircraft, chemical, and biological systems. Unlike ordinary differential equations, time delayed systems are infinite dimensional in nature and time-delay is, in many cases, a source of instability. The stability issue and the performance of time delayed systems are, therefore, both of theoretical and practical importance. Since Mackey and Glass [11] first found chaos in time delayed system, there has been increasing interest in time delayed chaotic systems [12, 13]. The synchronization problem for time delayed chaotic systems is also investigated by several researchers [14–20].
In recent years, fuzzy logic methodology has been proven effective in dealing with complex nonlinear systems containing certainties that are otherwise difficult to model. Among various kinds of fuzzy methods, Takagi-Sugeno (T-S) fuzzy model provides a successful method to describe certain complex nonlinear systems using some local linear subsystems [21, 22]. In [23], a fuzzy feedback control method was proposed for chaotic synchronization and chaotic model following control. The authors in [24, 25] proposed fuzzy observer-based chaotic synchronization and secure communication. In [26, 27], fuzzy adaptive synchronization methods for chaotic systems with unknown parameters were proposed. In spite of these advances in T-S fuzzy model-based chaos control and synchronization, most works were restricted to chaotic systems without time-delay. Due to finite signal transmission times, switching speeds and memory effects, time delayed systems are ubiquitous in nature, technology, and society [28, 29]. Time delayed chaotic systems are also interesting because the dimension of their chaotic dynamics can be increased by increasing the delay time sufficiently [30]. For this reason, the time delayed chaotic system has been suggested as a good candidate for secure communication [31]. The dimension of solution space of time delayed chaotic systems is infinite and so more than one positive Lyapunov exponents could be produced just by some low-dimension delayed chaotic systems. Therefore, communication system with a higher security level can be designed by means of time delayed chaotic systems. In addition, the time delayed system can be considered as a special case of spatiotemporal system [32]. From the above point of view, we can see that the study of fuzzy synchronization of time delayed chaotic systems is of high practical importance. To the best of our knowledge, however, for the fuzzy synchronization problem of time delayed chaotic systems, there is no result in the literature so far, which still remains open and challenging. This situation motivates our present investigation.
Motivated by the above discussions, the aim of this paper is to investigate the fuzzy adaptive exponential synchronization problem for time delayed chaotic systems with unknown parameters. T-S fuzzy model is adopted for the modeling of time delayed chaotic drive and response systems. Based on this fuzzy model, a new fuzzy synchronization controller is designed and an analytic expression of the controller with its adaptive laws of parameters is shown. By the proposed scheme, the closed-loop error system is adaptively exponentially synchronized. By virtue of Lyapunov-Krasovskii stability theory, linear matrix inequality (LMI) approach, and Jesen's inequality, an existence criterion for the proposed controller is represented in terms of the LMI, that can be readily checked by using some standard numerical packages [33].
This paper is organized as follows. In Section 2, we formulate the problem. In Section 3, a fuzzy adaptive exponential synchronization controller is proposed for time delayed chaotic systems with unknown parameters. In Section 4, an application example for time delayed Lorenz system is given, and finally, conclusions are presented in Section 5.
2. Problem Formulation
Consider a class of uncertain time delayed chaotic systems described by the following.

where  is the state vector,
is the state vector,  is the time-delay of the chaotic system (2.1),
is the time-delay of the chaotic system (2.1),  and
and  are known constant matrices,
are known constant matrices,  denotes a bias term which is generated by the fuzzy modeling procedure,
denotes a bias term which is generated by the fuzzy modeling procedure,  and
and  are activation function matrices,
are activation function matrices,  and
and  represent the uncertain constant parameter vectors,
represent the uncertain constant parameter vectors,  is the premise variable,
is the premise variable,  is the fuzzy set that is characterized by membership function,
is the fuzzy set that is characterized by membership function,  is the number of the IF-THEN rules, and
is the number of the IF-THEN rules, and  is the number of the premise variables.
is the number of the premise variables.
Using a standard fuzzy inference method (using a singleton fuzzifier, product fuzzy inference, and weighted average defuzzifier), the system (2.1) is inferred as follows:

where  ,
,  ,
,  is the membership function of the system with respect to the fuzzy rule
is the membership function of the system with respect to the fuzzy rule  .
.  can be regarded as the normalized weight of each IF-THEN rule and it satisfies
can be regarded as the normalized weight of each IF-THEN rule and it satisfies

The system (2.2) is considered as a drive system. The synchronization problem of system (2.2) is considered by using the drive-response configuration. According to the drive-response concept, the controlled fuzzy response system is described by the following rules.

where  is the state vector of the response system and
is the state vector of the response system and  is the control input. The fuzzy response system can be inferred as
is the control input. The fuzzy response system can be inferred as

Define the synchronization error  . Then we obtain the synchronization error system
. Then we obtain the synchronization error system

Throughout this paper, we define that  and
and  are the estimate values of
are the estimate values of  and
and  , respectively.
, respectively.
Definition 2.1 (Adaptive exponential synchronization).
With nonzero initial conditions, the error system (2.6) is adaptively exponentially synchronized if the synchronization error  satisfies
satisfies

where  and
and  are positive constants, under the control
are positive constants, under the control  with the adaptive laws
with the adaptive laws  and
and  ,
,  .
.
The purpose of this paper is to design the controller  with the adaptive laws
with the adaptive laws  and
and  ,
,  guaranteeing the adaptive exponential synchronization for time delayed chaotic systems with unknown parameters.
guaranteeing the adaptive exponential synchronization for time delayed chaotic systems with unknown parameters.
3. An LMI-Based Fuzzy Adaptive Exponential Synchronization
In this section, we present the LMI problem for achieving the fuzzy adaptive exponential synchronization of time delayed chaotic systems with unknown parameters.
Theorem 3.1.
If there exist  ,
,  ,
,  ,
,  ,
,  , and
, and  such that
such that

for  , where
, where  is an enough small real number properly selected, then the fuzzy adaptive exponential synchronization is achieved under the control
is an enough small real number properly selected, then the fuzzy adaptive exponential synchronization is achieved under the control

and the adaptive laws

where  and
and  are positive definite matrices for design.
are positive definite matrices for design.
Proof.
The fuzzy adaptive exponential synchronization controller can be constructed via the parallel distributed compensation. The controller is described by the following rules.

where  is the gain matrix of the controller for the fuzzy rule
is the gain matrix of the controller for the fuzzy rule  . The fuzzy controller can be inferred as
. The fuzzy controller can be inferred as

The closed-loop error system with the control input (3.5) can be written as

where  and
and  . Consider the following Lyapunov-Krasovskii functional:
. Consider the following Lyapunov-Krasovskii functional:

The time derivative of  along the trajectory of (3.6) is
along the trajectory of (3.6) is

Using the Jesen's inequality [34], we have

Finally, using (3.9), the time derivative of  can be obtained as
can be obtained as

where

If the adaptive laws (3.3) are used and the following matrix inequality is satisfied:

for  , then we have
, then we have

That is,  for all
for all  . Thus, it implies that
. Thus, it implies that  for any
for any  . In addition, from (3.7), one has
. In addition, from (3.7), one has

Also, we have

where  is the minimum eigenvalue of the matrix
is the minimum eigenvalue of the matrix  . It follows immediately from (3.14) and (3.15) that
. It follows immediately from (3.14) and (3.15) that

If we let

we obtain (2.7). If we let  , (3.12) is equivalently changed into the LMI (3.1), then the gain matrix of the control input
, (3.12) is equivalently changed into the LMI (3.1), then the gain matrix of the control input  is given by
is given by  . This completes the proof.
. This completes the proof.
Remark 3.2.
Various efficient convex optimization algorithms can be used to check whether the LMI (3.1) is feasible. In this paper, in order to solve the LMI, we utilize MATLAB LMI Control Toolbox [35], which implements state-of- the-art interior-point algorithms.
4. Numerical Example
Consider the following time delayed Lorenz system [36]:

The parameter  is assumed unknown. By defining two fuzzy sets, we can obtain the following fuzzy drive system that exactly represents the nonlinear equation of the time delayed Lorenz system under the assumption that
is assumed unknown. By defining two fuzzy sets, we can obtain the following fuzzy drive system that exactly represents the nonlinear equation of the time delayed Lorenz system under the assumption that  with
with  :
:

where

The membership functions are

For the numerical simulation, we use parameters  ,
,  , and
, and  . Applying Theorem 3.1 to the fuzzy system (4.2) yields
. Applying Theorem 3.1 to the fuzzy system (4.2) yields

Figure 1 shows state trajectories when the initial conditions are given by  ,
,  , and
, and  . From Figure 1, it can be seen that drive and response systems are indeed achieving chaos synchronization. Figure 2 plots the time responses of synchronization errors. The estimate
. From Figure 1, it can be seen that drive and response systems are indeed achieving chaos synchronization. Figure 2 plots the time responses of synchronization errors. The estimate  of the uncertain parameter
of the uncertain parameter  is illustrated at Figure 3, which shows that the estimate
is illustrated at Figure 3, which shows that the estimate  approaches rapidly to target value
approaches rapidly to target value  . Simulation results reveal that the response system controlled using the proposed synchronization method performs well. The effectiveness and accuracy of the proposed method is demonstrated.
. Simulation results reveal that the response system controlled using the proposed synchronization method performs well. The effectiveness and accuracy of the proposed method is demonstrated.
5. Conclusion
In this paper, a new fuzzy adaptive exponential synchronization scheme, which consists of time delayed fuzzy drive and response systems, is proposed for time delayed chaotic systems with unknown parameters. Based on Lyapunov-Krasovskii stability theory and LMI formulation, the proposed scheme can guarantee the adaptive exponential synchronization. The synchronization problem for the time delayed Lorenz system is given to illustrate the effectiveness of the proposed scheme. Finally, the proposed synchronization method has the advantage that it can be effectively used to adaptive exponential control and synchronization of other uncertain time delayed nonlinear systems described by a T-S fuzzy model.
References
Fujisaka H, Yamada T: Stability theory of synchronized motion in coupled-oscillator systems. Progress of Theoretical Physics 1983, 69(1):32–47. 10.1143/PTP.69.32
Pecora LM, Carroll TL: Synchronization in chaotic systems. Physical Review Letters 1990, 64(8):821–824. 10.1103/PhysRevLett.64.821
Chen G, Dong X: From Chaos to Order: Methodologies, Perspectives and Applications, World Scientific Series on Nonlinear Science. Series A: Monographs and Treatises. Volume 24. World Scientific, River Edge, NJ, USA; 1998:xxii+753.
Wang C-C, Su J-P: A new adaptive variable structure control for chaotic synchronization and secure communication. Chaos, Solitons and Fractals 2004, 20(5):967–977. 10.1016/j.chaos.2003.10.026
Ott E, Grebogi C, Yorke JA: Controlling chaos. Physical Review Letters 1990, 64(11):1196–1199. 10.1103/PhysRevLett.64.1196
Yang X-S, Chen G: Some observer-based criteria for discrete-time generalized chaos synchronization. Chaos, Solitons and Fractals 2002, 13(6):1303–1308. 10.1016/S0960-0779(01)00127-8
Bai E-W, Lonngren KE: Synchronization of two Lorenz systems using active control. Chaos, Solitons and Fractals 1997, 8(1):51–58. 10.1016/S0960-0779(96)00060-4
Hu J, Chen S, Chen L: Adaptive control for anti-synchronization of Chua's chaotic system. Physics Letters A 2005, 339(6):455–460. 10.1016/j.physleta.2005.04.002
Ahn CK: An
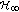 approach to anti-synchronization for chaotic systems. Physics Letters A 2009, 373(20):1729–1733. 10.1016/j.physleta.2009.03.032
approach to anti-synchronization for chaotic systems. Physics Letters A 2009, 373(20):1729–1733. 10.1016/j.physleta.2009.03.032Ahn CK: A passivity approach to synchronization for time-delayed chaotic systems. Modern Physics Letters B 2009, 23(29):3531–3541. 10.1142/S0217984909021594
Mackey MC, Glass L: Oscillation and chaos in physiological control systems. Science 1977, 197(4300):287–289. 10.1126/science.267326
Farmer JD: Chaotic attractors of an infinite-dimensional dynamical system. Physica D 1981/82, 4(3):366–393.
Lu H: Chaotic attractors in delayed neural networks. Physics Letters A 2002, 298(2–3):109–116. 10.1016/S0375-9601(02)00538-8
Tian Y-C, Gao F: Adaptive control of chaotic continuous-time systems with delay. Physica D 1998, 117(1–4):1–12.
Park JH, Kwon OM: Guaranteed cost control of time-delay chaotic systems. Chaos, Solitons and Fractals 2006, 27(4):1011–1018. 10.1016/j.chaos.2005.04.076
Chen B, Liu X, Tong S: Guaranteed cost control of time-delay chaotic systems via memoryless state feedback. Chaos, Solitons and Fractals 2007, 34(5):1683–1688. 10.1016/j.chaos.2006.05.009
Guan X, Feng G, Chen C, Chen G: A full delayed feedback controller design method for time-delay chaotic systems. Physica D 2007, 227(1):36–42. 10.1016/j.physd.2006.12.009
Chen M, Chen W-H: Robust adaptive neural network synchronization controller design for a class of time delay uncertain chaotic systems. Chaos, Solitons and Fractals 2009, 41(5):2716–2724. 10.1016/j.chaos.2008.10.003
Zhu W, Xu D, Huang Y: Global impulsive exponential synchronization of time-delayed coupled chaotic systems. Chaos, Solitons and Fractals 2008, 35(5):904–912. 10.1016/j.chaos.2006.05.078
Liu X: Impulsive synchronization of chaotic systems subject to time delay. Nonlinear Analysis: Theory, Methods and Applications 2009, 71(12):e1320-e1327. 10.1016/j.na.2009.01.162
Takagi T, Sugeno M: Fuzzy identification of systems and its applications to modeling and control. IEEE Transactions on Systems, Man and Cybernetics 1985, 15(1):116–132.
Tanaka K, Sugeno M: Stability analysis and design of fuzzy control systems. Fuzzy Sets and Systems 1992, 45(2):135–156. 10.1016/0165-0114(92)90113-I
Tanaka K, Ikeda T, Wang HO: A unified approach to controlling chaos via an LMI-based fuzzy control system design. IEEE Transactions on Circuits and Systems. I 1998, 45(10):1021–1040. 10.1109/81.728857
Lian K-Y, Chiu C-S, Chiang T-S, Liu P: LMI-based fuzzy chaotic synchronization and communications. IEEE Transactions on Fuzzy Systems 2001, 9(4):539–553. 10.1109/91.940967
Lian K-Y, Chiang T-S, Chiu C-S, Liu P: Synthesis of fuzzy model-based designs to synchronization and secure communications for chaotic systems. IEEE Transactions on Systems, Man, and Cybernetics Part B 2001, 31(1):66–83.
Kim J-H, Park C-W, Kim E, Park M: Adaptive synchronization of T-S fuzzy chaotic systems with unknown parameters. Chaos, Solitons and Fractals 2005, 24(5):1353–1361. 10.1016/j.chaos.2004.09.082
Kim J-H, Hyun C-H, Kim E, Park M: Adaptive synchronization of uncertain chaotic systems based on T-S fuzzy model. IEEE Transactions on Fuzzy Systems 2007, 15(3):359–369.
Traub RD, Miles R, Wong RKS: Model of the origin of rhythmic population oscillations in the hippocampal slice. Science 1989, 243(4896):1319–1325. 10.1126/science.2646715
Foss J, Longtin A, Mensour B, Milton J: Multistability and delayed recurrent loops. Physical Review Letters 1996, 76(4):708–711. 10.1103/PhysRevLett.76.708
Pyragas K: Synchronization of coupled time-delay systems: analytical estimations. Physical Review E 1998, 58(3):3067–3071. 10.1103/PhysRevE.58.3067
Pyragas K: Transmission of signals via synchronization of chaotic time-delay systems. International Journal of Bifurcation and Chaos 1998, 8: 1839–1842. 10.1142/S0218127498001558
Masoller C: Spatiotemporal dynamics in the coherence collapsed regime of semiconductor lasers with optical feedback. Chaos 1997, 7(3):455–462. 10.1063/1.166253
Boyd S, El Ghaoui L, Feron E, Balakrishnan V: Linear Matrix Inequalities in System and Control Theory, SIAM Studies in Applied Mathematics. Volume 15. SIAM, Philadelphia, Pa, USA; 1994:xii+193.
Noldus E: Stabilization of a class of distributional convolution equations. International Journal of Control 1985, 41(4):947–960. 10.1080/0020718508961174
Gahinet P, Nemirovski A, Laub AJ, Chilali M: LMI Control Toolbox. The Mathworks; 1995.
Li L, Peng H, Yang Y, Wang X: On the chaotic synchronization of Lorenz systems with time-varying lags. Chaos, Solitons and Fractals 2009, 41(2):783–794. 10.1016/j.chaos.2008.03.014
Acknowledgment
This work was supported by the grant of the Korean Ministry of Education, Science and Technology (The Regional Core Research Program/Center for Healthcare Technology Development).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ahn, C. A T-S Fuzzy Model-Based Adaptive Exponential Synchronization Method for Uncertain Delayed Chaotic Systems: An LMI Approach. J Inequal Appl 2010, 168962 (2010). https://doi.org/10.1155/2010/168962
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/168962



 of parameter
of parameter  .
.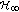 approach to anti-synchronization for chaotic systems. Physics Letters A 2009, 373(20):1729–1733. 10.1016/j.physleta.2009.03.032
approach to anti-synchronization for chaotic systems. Physics Letters A 2009, 373(20):1729–1733. 10.1016/j.physleta.2009.03.032