- Research Article
- Open access
- Published:
Local Boundedness of Weak Solutions for Nonlinear Parabolic Problem with 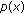 -Growth
-Growth
Journal of Inequalities and Applications volume 2010, Article number: 163269 (2010)
Abstract
We study the nonlinear parabolic problem with  -growth conditions in the space
-growth conditions in the space  and give a local boundedness theorem of weak solutions for the following equation
and give a local boundedness theorem of weak solutions for the following equation  , where
, where  and
and  satisfy
satisfy  -growth conditions with respect to
-growth conditions with respect to  and
and  .
.
1. Introduction
The study of variational problems with nonstandard growth conditions is an interesting topic in recent years.  -growth problems can be regarded as a kind of nonstandard growth problems and they appear in nonlinear elastic, electrorheological fluids and other physics phenomena. Many results have been obtained on this kind of problems, for example [1–9].
-growth problems can be regarded as a kind of nonstandard growth problems and they appear in nonlinear elastic, electrorheological fluids and other physics phenomena. Many results have been obtained on this kind of problems, for example [1–9].
Let  be
be  , where
, where  is given. In [8], the authors studied the following equation:
is given. In [8], the authors studied the following equation:

where  ,
,  is dependent on the space variable
is dependent on the space variable  and the time variable
and the time variable  ,
,  is the local weak solution in the space
is the local weak solution in the space  , and the authors proved the local boundedness of the local weak solution in
, and the authors proved the local boundedness of the local weak solution in  . In this paper, we will study the following more general problem:
. In this paper, we will study the following more general problem:



where  is a given function in
is a given function in  and
and  is an elliptic operator of the form
is an elliptic operator of the form  with the coefficients
with the coefficients  and
and  satisfying the classical Leray-Lions conditions. In [10], we have proved the existence of the solutions of (1.2)–(1.4) and have gotten
satisfying the classical Leray-Lions conditions. In [10], we have proved the existence of the solutions of (1.2)–(1.4) and have gotten  ; in this paper we will give the local boundedness theorem of the weak solutions in the framework space
; in this paper we will give the local boundedness theorem of the weak solutions in the framework space  , which can be considered as a special case of the space
, which can be considered as a special case of the space  .
.
Many authors have already studied the boundedness of weak solutions of parabolic equation with  -growth conditions, where
-growth conditions, where  is a constant, for example [8, 11–15]. The boundedness of the weak solutions plays a central role in many aspects. Based on the boundedness, we can further study the regularity of the solutions. For example, first in [15] the author studied the equation
is a constant, for example [8, 11–15]. The boundedness of the weak solutions plays a central role in many aspects. Based on the boundedness, we can further study the regularity of the solutions. For example, first in [15] the author studied the equation

and got  -estimates of the degenerate parabolic equation with
-estimates of the degenerate parabolic equation with  -growth conditions for
-growth conditions for  , where
, where  is a constant, then in [16] the authors established the Hölder continuity of the equation for the singular case
is a constant, then in [16] the authors established the Hölder continuity of the equation for the singular case  , and in [17] the authors discussed Harnack estimates for the bounded solutions of the above parabolic equation for
, and in [17] the authors discussed Harnack estimates for the bounded solutions of the above parabolic equation for  .
.
The space  provides a suitable framework to discuss some physical problems. In [18], the authors studied a functional with variable exponent,
provides a suitable framework to discuss some physical problems. In [18], the authors studied a functional with variable exponent,  , which provided a model for image denoising, enhancement, and restoration. Because in [18] the direction and speed of diffusion at each location depended on the local behavior,
, which provided a model for image denoising, enhancement, and restoration. Because in [18] the direction and speed of diffusion at each location depended on the local behavior,  only depended on the location
only depended on the location  in the image. Consider that the space
in the image. Consider that the space  was introduced and discussed in [10] and [19], we think that the space
was introduced and discussed in [10] and [19], we think that the space  is a reasonable framework to discuss the
is a reasonable framework to discuss the  -growth problem (1.2)–(1.4), where
-growth problem (1.2)–(1.4), where  only depends on the space variable
only depends on the space variable  similar to [18].
similar to [18].
In this paper, let  and
and  be the operators such that for any
be the operators such that for any  and
and  ,
,  and
and  are both continuous in
are both continuous in  for a.e.
for a.e.  and measurable in
and measurable in  for all
for all  . They also satisfy that for a.e.
. They also satisfy that for a.e.  , any
, any  and
and  :
:




where  are constants.
are constants.
Throughout this paper, unless special statement, we always suppose that  is
is  -continuous on
-continuous on  , that is,
, that is,  for every
for every  , and satisfy
, and satisfy


is the conjugate function of  .
.
Definition 1.1.
A function  is called a weak solution of (1.2)–(1.4) if
is called a weak solution of (1.2)–(1.4) if

for all  .
.
We will prove the following local boundedness theorem.
Theorem 1.2.
Let  . If
. If  is a nonnegative local weak solution of (1.2)–(1.4), then
is a nonnegative local weak solution of (1.2)–(1.4), then  is locally bounded in Q. Moreover, there exists a constant
is locally bounded in Q. Moreover, there exists a constant  such that for any
such that for any  and any
and any  ,
,

where for all  ,
,  ,
,  ,
,  , and
, and  .
.
2. Preliminaries
We first recall some facts on spaces  ,
,  , and
, and  . For the details, see [19–21].
. For the details, see [19–21].
Although we assume (1.10) holds in this paper, in this section we introduce the general spaces  ,
,  , and
, and  .
.
Denote

where  is an open subset.
is an open subset.
Let  be an element in
be an element in  . Denote
. Denote  . For
. For  , we define
, we define

The space  is
is

endowed with the norm

We define the conjugate function  of
of  by
by

Lemma 2.1 (see [21]).
-
(1)
The dual space of
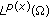 is
is 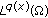 if
if 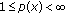 .
. -
(2)
The space
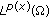 is reflexive if and only if (1.10) is satisfied.
is reflexive if and only if (1.10) is satisfied.
Lemma 2.2 (see [21]).
If  ,
,  is dense in the space
is dense in the space  and
and  is separable.
is separable.
Lemma 2.3 (see [21]).
Let  , for every
, for every  and
and  , we have
, we have

where C is only dependent on  and
and  , not dependent on
, not dependent on  .
.
Next let  be an integer. For each
be an integer. For each  ,
,  are nonnegative integers and
are nonnegative integers and  , and denote by
, and denote by  the distributional derivative of order
the distributional derivative of order  with respect to the variable
with respect to the variable  .
.
We now introduce the generalized Lebesgue-Sobolev space  which is defined as
which is defined as


is a Banach space endowed with the norm

The space  is defined as the closure of
is defined as the closure of  in
in  . The dual space
. The dual space  is denoted by
is denoted by  equipped with the norm
equipped with the norm

where infimum is taken on all possible decompositions

Lemma 2.4 (see [21]).
(1)  and
and  are separable if
are separable if  .
.
(2)  and
and  are reflexive if (1.10) holds.
are reflexive if (1.10) holds.
We define the space  as the following:
as the following:


is a Banach space with the norm  , where
, where  is independent of
is independent of  .
.
The space  is defined as the closure of
is defined as the closure of  in
in  , and
, and  is continuous embedding. Let
is continuous embedding. Let  be the number of multiindexes
be the number of multiindexes  which satisfies
which satisfies  , then the space
, then the space  can be considered as a close subspace of the product space
can be considered as a close subspace of the product space  . So if
. So if  ,
,  is reflexive and further we can get that the space
is reflexive and further we can get that the space  is reflexive. The dual space
is reflexive. The dual space  is denoted by
is denoted by  equipped with the norm
equipped with the norm

where infimum is taken on all possible decompositions

Next, we will introduce some results in [22].
Lemma 2.5.
Let  be a sequence of positive numbers, satisfying the inequalities
be a sequence of positive numbers, satisfying the inequalities  , where
, where  and
and  are given numbers. If
are given numbers. If  , then
, then  converges to 0 as
converges to 0 as  .
.
Lemma 2.6.
There exists a constant  depending only on
depending only on  , such that for every
, such that for every  ,
,

where  .
.
Remark 2.7.
In [10], we have gotten that for the Galerkin solutions  ,
,  strongly in
strongly in  ,
,  weakly in
weakly in  ,
,  weakly in
weakly in  and
and  weakly in
weakly in  .
.
3. Proof of the Theorem
Suppose that  is a weak solution of (1.2)–(1.4), then there exists
is a weak solution of (1.2)–(1.4), then there exists  such that
such that

Indeed, by Young's inequality, we have

where  is the Lebesgue measure of
is the Lebesgue measure of  . Since
. Since  and
and  , we can get
, we can get  . Then by Lemma 2.6, we get
. Then by Lemma 2.6, we get

where  . Thus the desired result is obtained.
. Thus the desired result is obtained.
We define  . Fix a point
. Fix a point  in
in  . Let
. Let  ,
,  , and
, and  . Fix
. Fix  and consider the sequences
and consider the sequences

and the corresponding cylinders  . It follows from the definitions that
. It follows from the definitions that

We consider also the boxes  , where for
, where for 

For these boxes, we have the inclusion

We introduce the sequence of increasing levels

Let  be the Galerkin solutions in [10]. Similarly, we can get
be the Galerkin solutions in [10]. Similarly, we can get  is bounded in
is bounded in  . Since
. Since  converges to 0 in
converges to 0 in  , by interpolation inequality, we have
, by interpolation inequality, we have

where  ,
,  . Furthermore,
. Furthermore,  strongly in
strongly in  . Since
. Since  ,
,  strongly in
strongly in  . In the same way, we obtain that
. In the same way, we obtain that  strongly in
strongly in  ; furthermore, we get
; furthermore, we get  for a.e.
for a.e.  .
.
Let  and
and  be the smooth cutoff function satisfying
be the smooth cutoff function satisfying

Take  as the testing function in the following equation:
as the testing function in the following equation:

First, by  for a.e.
for a.e.  and
and  strongly in
strongly in  , we get
, we get

By Fatou's lemma, we get

Because  strongly in
strongly in  and
and  weakly in
weakly in  , we get
, we get

Since  strongly in
strongly in  and
and  weakly in
weakly in  , we have
, we have

Then for the remaining parts of (3.11), we get

By (1.6), (1.7), and (1.9),

As  , by Young's inequality and Hölder's inequality, we have
, by Young's inequality and Hölder's inequality, we have

In the same way, by  and Young's inequality, we have
and Young's inequality, we have

For a set  , meas
, meas  is the Lebesgue measure of
is the Lebesgue measure of  . Let
. Let  and
and  . By (3.11)–(3.19), we get
. By (3.11)–(3.19), we get

Moreover, we observe that for  to be determined later,
to be determined later,

thus we get

Then for  and
and  in (3.22), by Hölder inequality, we obtain respectively
in (3.22), by Hölder inequality, we obtain respectively


For the integral involving  , first we write
, first we write  , then we obtain
, then we obtain

By Young's inequality and (3.25), we get

Let  , then
, then  . By (3.20)–(3.24) and (3.26), we obtain
. By (3.20)–(3.24) and (3.26), we obtain

By Young's inequality,

Moreover, by (3.27), we can get

Next we define the smooth cutoff function  in
in 

For the function  , by Lemma 2.6 and (3.29), we get
, by Lemma 2.6 and (3.29), we get

Finally, we define  ,
,  Let
Let  ; by Hölder inequality, we obtain
; by Hölder inequality, we obtain

where  . Then by Lemma 2.5, we have
. Then by Lemma 2.5, we have  as
as  , provided
, provided  is chosen to satisfy
is chosen to satisfy

By  , we can get
, we can get  as
as  . Since
. Since  and
and  a.e. in
a.e. in  , by Lebesuge's theorem we get
, by Lebesuge's theorem we get  . So we obtain
. So we obtain  a.e. in
a.e. in  .
.
Thus we get

Remark 3.1.
In this paper, we study the boundedness of weak solution in the case  . For the singular case
. For the singular case  , the conditions in the paper are not enough. In [22], there is a counterexample in
, the conditions in the paper are not enough. In [22], there is a counterexample in  13 of Chapter XII. The author studied the solutions of the homogeneous equation
13 of Chapter XII. The author studied the solutions of the homogeneous equation

where

and proved that the solution  is unbounded in
is unbounded in  .
.
Remark 3.2.
In general, we consider the equation

where


and  is an elliptic operator of the form
is an elliptic operator of the form  .
.  and
and  satisfy that for a.e.
satisfy that for a.e.  , any
, any  and
and  :
:

where  ,
,  , and
, and  are constants.
are constants.
Similarly, we can get the following theorem.
Theorem 3.3.
Let  . If
. If  is a nonnegative local weak solution of (3.37), (1.3), and (1.4), then
is a nonnegative local weak solution of (3.37), (1.3), and (1.4), then  is locally bounded in Q. Moreover, there exists a constant
is locally bounded in Q. Moreover, there exists a constant  such that for any
such that for any  and any
and any  ,
,

where for all  ,
,  ,
,  ,
,  , and
, and  ,
,  .
.
References
Acerbi E, Mingione G: Regularity results for stationary electro-rheological fluids. Archive for Rational Mechanics and Analysis 2002, 164(3):213–259. 10.1007/s00205-002-0208-7
Acerbi E, Mingione G: Gradient estimates for the -Laplacean system. Journal für die Reine und Angewandte Mathematik 2005, 584: 117–148.
Acerbi E, Mingione G: Gradient estimates for a class of parabolic systems. Duke Mathematical Journal 2007, 136(2):285–320. 10.1215/S0012-7094-07-13623-8
Mihăilescu M, Rădulescu V: On a nonhomogeneous quasilinear eigenvalue problem in Sobolev spaces with variable exponent. Proceedings of the American Mathematical Society 2007, 135(9):2929–2937. 10.1090/S0002-9939-07-08815-6
Mihăilescu M, Rădulescu V: A multiplicity result for a nonlinear degenerate problem arising in the theory of electrorheological fluids. Proceedings of the Royal Society of London A 2006, 462(2073):2625–2641. 10.1098/rspa.2005.1633
Rădulescu V: Exponential growth of a solution. The American Mathematical Monthly 2007, 114: 165–166.
Ruzicka M: Electrorheological Fluids: Modeling and Mathematical Theory, Lecture Notes in Mathematics. Volume 1748. Springer, Berlin, Germany; 2000:xvi+176.
Xu M, Chen YZ: Hölder continuity of weak solutions for parabolic equations with nonstandard growth conditions. Acta Mathematica Sinica. English Series 2006, 22(3):793–806. 10.1007/s10114-005-0582-9
Zhikov VV: Averaging of functionals of the calculus of variations and elasticity theory. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 1986, 50(4):675–710.
Fu Y, Pan N: Existence of solutions for nonlinear parabolic problem with -growth. Journal of Mathematical Analysis and Applications 2010, 362(2):313–326. 10.1016/j.jmaa.2009.08.038
Chen C: Global existence and estimates of solution for doubly nonlinear parabolic equation. Journal of Mathematical Analysis and Applications 2000, 244(1):133–146. 10.1006/jmaa.1999.6695
Chen YZ, DiBenedetto E: Boundary estimates for solutions of nonlinear degenerate parabolic systems. Journal für die Reine und Angewandte Mathematik 1989, 395: 102–131.
Cirmi GR, Porzio MM: -solutions for some nonlinear degenerate elliptic and parabolic equations. Annali di Matematica Pura ed Applicata. Serie Quarta 1995, 169: 67–86. 10.1007/BF01759349
Liu J, N'Guérékata G, Minh NV, Phong VQ: Bounded solutions of parabolic equations in continuous function spaces. Funkcialaj Ekvacioj 2006, 49(3):337–355. 10.1619/fesi.49.337
Porzio MM: -estimates for degenerate and singular parabolic equations. Nonlinear Analysis: Theory, Methods & Applications 1991, 17(11):1093–1107. 10.1016/0362-546X(91)90194-6
Chen YZ, DiBenedetto E: On the local behavior of solutions of singular parabolic equations. Archive for Rational Mechanics and Analysis 1988, 103(4):319–345.
DiBenedetto E, Gianazza U, Vespri V: Harnack estimates for quasi-linear degenerate parabolic differential equations. Acta Mathematica 2008, 200(2):181–209. 10.1007/s11511-008-0026-3
Chen Y, Levine S, Rao M: Variable exponent, linear growth functionals in image restoration. SIAM Journal on Applied Mathematics 2006, 66(4):1383–1406. 10.1137/050624522
Shi SJ, Chen ST, Wang YW: Some convergence theorems in the spaces and their conjugate spaces. Acta Mathematica Sinica. Chinese Series 2007, 50(5):1081–1086.
Fan X, Zhao D: On the spaces and . Journal of Mathematical Analysis and Applications 2001, 263(2):424–446. 10.1006/jmaa.2000.7617
Kovácik O, Rákosnik J: On spaces and . Czechoslovak Mathematical Journal 1991, 41: 592–618.
DiBenedetto E: Degenerate Parabolic Equations, Universitext. Springer, New York, NY, USA; 1993:xvi+387.
Acknowledgments
This work is supported by Science Research Foundation in Harbin Institute of Technology (HITC200702), and The Natural Science Foundation of Heilongjiang Province (A2007-04) and the Program of Excellent Team in Harbin Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fu, Y., Pan, N. Local Boundedness of Weak Solutions for Nonlinear Parabolic Problem with 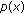 -Growth.
J Inequal Appl 2010, 163269 (2010). https://doi.org/10.1155/2010/163269
-Growth.
J Inequal Appl 2010, 163269 (2010). https://doi.org/10.1155/2010/163269
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/163269
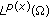 is
is 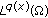 if
if 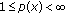 .
.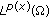 is reflexive if and only if (1.10) is satisfied.
is reflexive if and only if (1.10) is satisfied.