- Research Article
- Open access
- Published:
Symmetrization of Functions and the Best Constant of 1-DIM 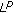 Sobolev Inequality
Sobolev Inequality
Journal of Inequalities and Applications volume 2009, Article number: 874631 (2009)
Abstract
The best constants  of Sobolev embedding of
of Sobolev embedding of  into
into  for
for  and
and  are obtained. A lemma concerning the symmetrization of functions plays an important role in the proof.
are obtained. A lemma concerning the symmetrization of functions plays an important role in the proof.
1. Introduction
Let  be a Sobolev space which consists of the functions whose derivatives up to
be a Sobolev space which consists of the functions whose derivatives up to  vanish at
vanish at  , that is,
, that is,

where  denotes
denotes  th derivative of
th derivative of  in a distributional sense. The purpose of this paper is to investigate the best constant
in a distributional sense. The purpose of this paper is to investigate the best constant  of
of  Sobolev inequality
Sobolev inequality

where  and
and  . The result is as follows.
. The result is as follows.
Theorem 1.1.
The best constant of inequality (1.2) is



where  satisfies
satisfies  and
and  in (1.5) is the unique solution of the equation
in (1.5) is the unique solution of the equation

satisfying  .
.
For special values of  , the solution of (1.6) can be written explicitly, and
, the solution of (1.6) can be written explicitly, and  is expressed as follows.
is expressed as follows.
Corollary 1.2.
One has

The best constants  and
and  were recently obtained by Oshime [1]. This paper gives an alternative proof which simplifies the derivation process of
were recently obtained by Oshime [1]. This paper gives an alternative proof which simplifies the derivation process of  and
and  and computes further constant
and computes further constant  . To compute these constants, the following lemma with respect to the symmetrization of functions plays an important role.
. To compute these constants, the following lemma with respect to the symmetrization of functions plays an important role.
Lemma 1.3.
Let  be an integer satisfying
be an integer satisfying  and let us define the functional
and let us define the functional  as follows:
as follows:

Then, for an arbitrary  , there exists an element
, there exists an element  which belongs to the following sub-space
which belongs to the following sub-space  of
of  :
:

such that

Remark 1.4.
The proof of this lemma (see Section 3) does not apply to the case  , since the relation
, since the relation

may fail to hold for  (see (3.4)–(3.6)). Hence the problem to obtain
(see (3.4)–(3.6)). Hence the problem to obtain  for
for  (essentially) still remains.
(essentially) still remains.
The existence of the maximizer of  can be seen in the proof of Theorem 1.1, where we construct it concretely, but here we would like to see this briefly though the proof of the following lemma.
can be seen in the proof of Theorem 1.1, where we construct it concretely, but here we would like to see this briefly though the proof of the following lemma.
Lemma 1.5.
Assume that the assertion of Lemma 1.3 holds, then the maximizer of  exists.
exists.
Proof.
Let  be sufficiently large, and let
be sufficiently large, and let  and
and  be as
be as

From Lemma 1.3, we see that if the maximizer exists, it is the element of  . So, we can restrict the definition domain of
. So, we can restrict the definition domain of  to
to  . Since
. Since  is convex and strongly closed (by Sobolev inequality) in
is convex and strongly closed (by Sobolev inequality) in  , it is weakly closed. In addition,
, it is weakly closed. In addition,  is weakly compact, so
is weakly compact, so  is also weakly compact. Moreover,
is also weakly compact. Moreover,  is weakly lower-semicontinuous in
is weakly lower-semicontinuous in  , and hence
, and hence  attains its minimum in
attains its minimum in  . This proves the lemma.
. This proves the lemma.
Finally, we introduce some studies related to the present paper. When  (Hilbertian Sobolev space case), the best constants for the embeddings of
(Hilbertian Sobolev space case), the best constants for the embeddings of  into
into  for various conditions were treated in Richardson [2], Kalyabin [3], and [4–8]; see also references of these literatures. On the other hand, for the case
for various conditions were treated in Richardson [2], Kalyabin [3], and [4–8]; see also references of these literatures. On the other hand, for the case  , few literature seems to be available. In [9], Kametaka, Oshime, Watanabe, Yamagishi, Nagai, and Takemura obtained the best constant of (1.2) when
, few literature seems to be available. In [9], Kametaka, Oshime, Watanabe, Yamagishi, Nagai, and Takemura obtained the best constant of (1.2) when  belongs to a subspace
belongs to a subspace  of
of  which consists of periodic functions
which consists of periodic functions

as

where  is a Bernoulli polynomial,
is a Bernoulli polynomial,  and
and  is an unique solution of the equation
is an unique solution of the equation

in the interval  . Moreover, in [1], Oshime obtained the best constant
. Moreover, in [1], Oshime obtained the best constant  and
and  . Other topics on this subject, especially the best constant of Sobolev inequalities on Riemannian manifolds, are seen in Hebey [10].
. Other topics on this subject, especially the best constant of Sobolev inequalities on Riemannian manifolds, are seen in Hebey [10].
2. Proof of Theorem 1.1
First, we prepare the following lemma.
Lemma 2.1.
Let  and
and  be a function satisfying
be a function satisfying

then, it holds that

where  is an arbitrary constant (later, in Lemma 2.3, one fixes the value of
is an arbitrary constant (later, in Lemma 2.3, one fixes the value of  to satisfy (1.6)).
to satisfy (1.6)).
Proof.
By integration by parts, we obtain the result.
From Lemma 1.3, to obtain the best constant of (1.2), we can restrict the definition domain of the functional  to the nonzero element of
to the nonzero element of  . Now, let
. Now, let  , then from Lemma 2.1 and Hölder's inequality, we have for
, then from Lemma 2.1 and Hölder's inequality, we have for  ,
,

So, we have

and the equality holds in (2.4) if and only if there exists  satisfying
satisfying

To confirm the existence of such  , we use the following lemmas.
, we use the following lemmas.
Lemma 2.2.
Let  satisfy
satisfy

then the solution  of
of

exists in  .
.
Proof.
Let us define  as
as

Clearly  is
is  and
and

Moreover, from the assumption, it holds that  .
.
Lemma 2.3.
The solution  of (1.6) uniquely exists.
of (1.6) uniquely exists.
Proof.
Let

Since

the assertion is proved.
Using Lemma 2.2 and 5, we obtain the following lemma.
Lemma 2.4.
Let  be a solution of (1.6) (when
be a solution of (1.6) (when  ), then the solution of (2.5) belongs to
), then the solution of (2.5) belongs to  for
for  .
.
Proof.
First, we prove the case  and
and  . For simplicity, let us put
. For simplicity, let us put  . Note that in these cases
. Note that in these cases  is a continuous function on
is a continuous function on  .
.

In the case  ,
,  is an even function, so integration of
is an even function, so integration of  over the interval
over the interval  vanishes. In addition,
vanishes. In addition,

holds, so the integration of  over the interval
over the interval  also vanishes. Hence, by Lemma 2.2, the solution
also vanishes. Hence, by Lemma 2.2, the solution  of (2.5) belongs to
of (2.5) belongs to  . Properties
. Properties  and
and  follow from the fact that
follow from the fact that  is an even function and (2.12). So, we have proven
is an even function and (2.12). So, we have proven  .
.

In the case ,
, is an odd function, so integrations of
is an odd function, so integrations of and
and over the interval
over the interval vanish. Moreover, from (1.6), the integration of
vanish. Moreover, from (1.6), the integration of over the interval
over the interval also vanishes. Hence, again by Lemma 2.2, we have the solution of (2.5) which belongs to
also vanishes. Hence, again by Lemma 2.2, we have the solution of (2.5) which belongs to . The remaining part is the same as case (i).
. The remaining part is the same as case (i).

In the case  , let us define
, let us define  as follows:
as follows:

Clearly it holds that  satisfies (2.5) (a.e.),
satisfies (2.5) (a.e.),  ,
,  and
and  . To see
. To see  , let
, let  be an arbitrary element of
be an arbitrary element of  . Since
. Since

we have, in a distributional sense,

Therefore,  . This proves the case
. This proves the case  .
.
Proof of Theorem 1.1.
From Lemma 1.3, and the argument of this section, especially Lemma 2.4,  . This proves Theorem 1.1.
. This proves Theorem 1.1.
Proof.
In this case, (1.6) becomes

So, we can explicitly solve this equation with respect to  . Substituting to (1.5), we obtain the result.
. Substituting to (1.5), we obtain the result.
3. Proof of Lemma 1.3
Now, all we have to do is to prove Lemma 1.3.
Proof of Lemma 1.3.
To avoid the complexity of notation, in the follwings, we fix  . Let
. Let  be an arbitrary element of
be an arbitrary element of  (
( ), and let
), and let

Here, we can assume  , since if it does not,
, since if it does not,  can be replaced by
can be replaced by  .
.
-
(i)
There is the case

Let us define  as
as

We have



when  , (3.4) and (3.5) when
, (3.4) and (3.5) when  , and (3.4) when
, and (3.4) when  . Further, let us define
. Further, let us define

Then  , since
, since  ,
,  . Moreover, from (3.2), we have
. Moreover, from (3.2), we have  . In addition, clearly
. In addition, clearly  . So, in the case (i), we have proven the lemma.
. So, in the case (i), we have proven the lemma.
-
(ii)
There is the case

Let  be an element satisfying
be an element satisfying  , and let
, and let

Further, let  be
be

So,

and hence we obtain

By putting  the right-hand side of (3.12) becomes
the right-hand side of (3.12) becomes

Similarly, let us put

and define  as
as

So,

and hence we obtain

By putting  the right-hand side of (3.17) becomes
the right-hand side of (3.17) becomes

Let us put

and define

Note that

The derivative of  is
is

-
(a)
The case

In this case, we have

Since

from the assumption (3.23),  is monotone increasing. So, we have
is monotone increasing. So, we have

But, from (3.23), it holds that

So, if we put

as case (i), we have  and
and  . In addition,
. In addition,  =
=  . So, we have proven the case (ii)-(a).
. So, we have proven the case (ii)-(a).
-
(b)
The case

In this case, we have

Moreover

since we have (3.29) and the assumption (3.8) ( ), respectively. Therefore, there exists
), respectively. Therefore, there exists  such that
such that  . Let us define the constant
. Let us define the constant  as
as

then  . Now we have
. Now we have

since

Let us define  as
as

Then, again as case (i), we have  and by (3.33),
and by (3.33),  . In addition,
. In addition,  . So, we have proven the case (ii)-(b). This completes the proof.
. So, we have proven the case (ii)-(b). This completes the proof.
References
Oshime Y: On the best constant for
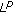 Sobolev inequalities. Scientiae Mathematicae Japonicae 2008,68(3):333–344.
Sobolev inequalities. Scientiae Mathematicae Japonicae 2008,68(3):333–344.Richardson W: Steepest descent and the least
 for Sobolev's inequality. The Bulletin of the London Mathematical Society 1986,18(5):478–484. 10.1112/blms/18.5.478
for Sobolev's inequality. The Bulletin of the London Mathematical Society 1986,18(5):478–484. 10.1112/blms/18.5.478Kalyabin GA: Sharp constants in inequalities for intermediate derivatives (the Gabushin case). Functional Analysis and Its Applications 2004,38(3):184–191.
Kametaka Y, Watanabe K, Nagai A, Pyatkov S: The best constant of Sobolev inequality in an
 dimensional Euclidean space. Scientiae Mathematicae Japonicae 2005,61(1):15–23.
dimensional Euclidean space. Scientiae Mathematicae Japonicae 2005,61(1):15–23.Kametaka Y, Yamagishi H, Watanabe K, Nagai A, Takemura K: Riemann zeta function, Bernoulli polynomials and the best constant of Sobolev inequality. Scientiae Mathematicae Japonicae 2007,65(3):333–359.
Nagai A, Takemura K, Kametaka Y, Watanabe K, Yamagishi H: Green function for boundary value problem of
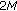 -th order linear ordinary differential equations with free boundary condition. Far East Journal of Applied Mathematics 2007,26(3):393–406.
-th order linear ordinary differential equations with free boundary condition. Far East Journal of Applied Mathematics 2007,26(3):393–406.Kametaka Y, Yamagishi H, Watanabe K, Nagai A, Takemura K: The best constant of Sobolev inequality corresponding to Dirichlet boundary value problem for
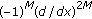 . Scientiae Mathematicae Japonicae 2008,68(3):299–311.
. Scientiae Mathematicae Japonicae 2008,68(3):299–311.Watanabe K, Kametaka Y, Nagai A, Takemura K, Yamagishi H: The best constant of Sobolev inequality on a bounded interval. Journal of Mathematical Analysis and Applications 2008,340(1):699–706. 10.1016/j.jmaa.2007.08.054
Kametaka Y, Oshime Y, Watanabe K, Yamagishi H, Nagai A, Takemura K: The best constant of
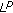 Sobolev inequality corresponding to the periodic boundary value problem for
Sobolev inequality corresponding to the periodic boundary value problem for  Scientiae Mathematicae Japonicae 2007,66(2):169–181.
Scientiae Mathematicae Japonicae 2007,66(2):169–181.Hebey E: Nonlinear Analysis on Manifolds: Sobolev Spaces and Inequalities, Courant Lecture Notes in Mathematics. Volume 5. New York University Courant Institute of Mathematical Sciences, New York, NY, USA; 1999:x+309.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Watanabe, K., Kametaka, Y., Nagai, A. et al. Symmetrization of Functions and the Best Constant of 1-DIM 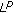 Sobolev Inequality.
J Inequal Appl 2009, 874631 (2009). https://doi.org/10.1155/2009/874631
Sobolev Inequality.
J Inequal Appl 2009, 874631 (2009). https://doi.org/10.1155/2009/874631
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/874631
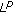 Sobolev inequalities. Scientiae Mathematicae Japonicae 2008,68(3):333–344.
Sobolev inequalities. Scientiae Mathematicae Japonicae 2008,68(3):333–344. for Sobolev's inequality. The Bulletin of the London Mathematical Society 1986,18(5):478–484. 10.1112/blms/18.5.478
for Sobolev's inequality. The Bulletin of the London Mathematical Society 1986,18(5):478–484. 10.1112/blms/18.5.478 dimensional Euclidean space. Scientiae Mathematicae Japonicae 2005,61(1):15–23.
dimensional Euclidean space. Scientiae Mathematicae Japonicae 2005,61(1):15–23.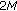 -th order linear ordinary differential equations with free boundary condition. Far East Journal of Applied Mathematics 2007,26(3):393–406.
-th order linear ordinary differential equations with free boundary condition. Far East Journal of Applied Mathematics 2007,26(3):393–406.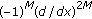 . Scientiae Mathematicae Japonicae 2008,68(3):299–311.
. Scientiae Mathematicae Japonicae 2008,68(3):299–311.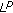 Sobolev inequality corresponding to the periodic boundary value problem for
Sobolev inequality corresponding to the periodic boundary value problem for  Scientiae Mathematicae Japonicae 2007,66(2):169–181.
Scientiae Mathematicae Japonicae 2007,66(2):169–181.