- Research Article
- Open access
- Published:
Existence of Solutions to the System of Generalized Implicit Vector Quasivariational Inequality Problems
Journal of Inequalities and Applications volume 2009, Article number: 654370 (2009)
Abstract
We study the system of generalized implicit vector quasivariational inequality problems and prove a new existence result of its solutions by Kakutani-Fan-Glicksberg's fixed points theorem. As a special case, we also derive a new existence result of solutions to the generalized implicit vector quasivariational inequality problems.
1. Introduction
The system of generalized implicit vector quasivariational inequality problems generalizes the generalized implicit vector quasivariational inequality problems, and the latter had been studied in [1–3]. In this paper, we study the system of generalized implicit vector quasivariational inequality problems and prove a new existence result of its solutions by Kakutani-Fan-Glicksberg's fixed points theorem. For other existence results with respect to the system of generalized implicit vector quasivariational inequality problems, we refer the reader to [4–6] and references therein.
Let  be an index set (finite or infinite). For each
be an index set (finite or infinite). For each  , let
, let  and
and  be two Hausdorff topological vector spaces,
be two Hausdorff topological vector spaces,  a nonempty subset of
a nonempty subset of  , and
, and  a closed, convex and pointed cone of
a closed, convex and pointed cone of  with
with  , where
, where  denotes the interior of
denotes the interior of  . Denote that
. Denote that  ,
,  . For each
. For each  , we can write
, we can write  . For each
. For each  , let
, let  be a nonempty subset of the continuous linear operators space
be a nonempty subset of the continuous linear operators space  from
from  into
into  and let
and let  ,
,  ,
,  be three set-valued maps, where
be three set-valued maps, where  and
and  denote the family of all nonempty subsets of
denote the family of all nonempty subsets of  and
and  , respectively. The system of generalized implicit vector quasivariational inequality problems (briefly, SGIVQIP) is as follows: find
, respectively. The system of generalized implicit vector quasivariational inequality problems (briefly, SGIVQIP) is as follows: find  such that for each
such that for each  and
and


is said to be a solution of the SGIVQIP. An SGIVQIP is usually denoted by  .
.
If  is a singleton, then the SGIVQIP coincides with the generalized implicit vector quasivariational inequality problems (briefly, GIVQIP). A GIVQIP is usually denoted by
is a singleton, then the SGIVQIP coincides with the generalized implicit vector quasivariational inequality problems (briefly, GIVQIP). A GIVQIP is usually denoted by  .
.
Throughout this paper, unless otherwise specified, assume that for each  ,
,  is a nonempty convex compact subset of a Banach space
is a nonempty convex compact subset of a Banach space 
 is a Hausdorff topological vector space, and
is a Hausdorff topological vector space, and  is a closed, convex, and pointed cone of
is a closed, convex, and pointed cone of  with
with  , where
, where  denotes the interior of
denotes the interior of  .
.
2. Preliminaries
In this section, we introduce some useful notations and results.
Definition 2.1.
Let  and
and  be two topological spaces and
be two topological spaces and  a nonempty convex subset of
a nonempty convex subset of  .
.  is a set-valued map.
is a set-valued map.
(1) is called upper semicontinuous at
is called upper semicontinuous at  if, for any open set
if, for any open set  , there exists an open neighborhood
, there exists an open neighborhood  of
of  in
in  such that for all
such that for all  ,
,

and upper semicontinuous on  if it is upper semicontinuous at every point of
if it is upper semicontinuous at every point of 
(2) is called lower semicontinuous at
is called lower semicontinuous at  if, for any open set
if, for any open set  , there exists an open neighborhood
, there exists an open neighborhood  of
of  in
in  such that for all
such that for all  ,
,

and lower semicontinuous on  if it is lower semicontinuous at every point of
if it is lower semicontinuous at every point of 
(3) is called continuous at
is called continuous at  if, it is both upper semicontinuous and lower semicontinuous at
if, it is both upper semicontinuous and lower semicontinuous at  ; and continuous on
; and continuous on  if it is continuous at every point of
if it is continuous at every point of  .
.
Definition 2.2.
Let  and
and  be two topological vector spaces and
be two topological vector spaces and  a nonempty convex subset of
a nonempty convex subset of  .Also
.Also  is a set-valued map.
is a set-valued map.
(1) is called upper
is called upper  semicontinuous at
semicontinuous at  if, for any open neighborhood
if, for any open neighborhood  of the zero element
of the zero element  in
in  , there exists an open neighborhood
, there exists an open neighborhood  of
of  in
in  such that, for all
such that, for all  ,
,

and upper  semicontinuous on
semicontinuous on  if it is upper
if it is upper  semicontinuous at every point of
semicontinuous at every point of  .
.
(2) is called lower
is called lower  semicontinuous at
semicontinuous at  if, for any open neighborhood V of the zero element
if, for any open neighborhood V of the zero element  in
in  , there exists an open neighborhood
, there exists an open neighborhood  of
of  in
in  such that, for all
such that, for all  ,
,

and lower  semicontinuous on
semicontinuous on  if it is lower
if it is lower  semicontinuous at every point of
semicontinuous at every point of  .
.
(3) is called
is called  continuous at
continuous at  if it is upper
if it is upper  semicontinuous and lower
semicontinuous and lower  semicontinuous at
semicontinuous at  ; and
; and  continuous on
continuous on  if it is
if it is  continuous at every point of
continuous at every point of  .
.
Definition 2.3.
Let  and
and  be two topological vector spaces and
be two topological vector spaces and  a nonempty convex subset of
a nonempty convex subset of  . Let
. Let  be a set-valued map.
be a set-valued map.
(1) is called
is called  convex if, for each
convex if, for each 
 ,
,

and  concave if
concave if  is
is  convex.
convex.
(2) is called
is called  quasiconvex-like if, for each
quasiconvex-like if, for each  ,
,  ,
,

and  quasiconcave-like if
quasiconcave-like if  is
is  quasiconvex-like.
quasiconvex-like.
Lemma 2.4 ([7, Theorem 1]).
Let  be a nonempty paracompact subset of a Hausdorff topological space
be a nonempty paracompact subset of a Hausdorff topological space  and,
and,  be a nonempty subset of a Hausdorff topological vector space
be a nonempty subset of a Hausdorff topological vector space  . Suppose that
. Suppose that  be two set-valued maps with following conditions:
be two set-valued maps with following conditions:
(1)for each  ,
,  ;
;
-
(2)
for each
 ,
, 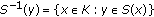 is open.
is open.
Then  has a continuous selection, that is, there is a continuous map
has a continuous selection, that is, there is a continuous map  such that
such that  for each
for each  .
.
3. Existence of Solutions to the SGIVQIP
Lemma 3.1.
Let  be three Hausdorff topological spaces,
be three Hausdorff topological spaces,  a topological vector space, and
a topological vector space, and  a closed, convex, and pointed cone of
a closed, convex, and pointed cone of  . Let
. Let  and
and  be two set-valued maps. Assume that
be two set-valued maps. Assume that  and
and
(1) is upper semicontinuous on
is upper semicontinuous on  with nonempty and compact values;
with nonempty and compact values;
(2) is upper
is upper  semicontinuous on
semicontinuous on  with nonempty and compact values;
with nonempty and compact values;
-
(3)
for each
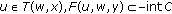 .
.
Then there exist open neighborhood  of
of  and open neighborhood
and open neighborhood  of
of  , and open neighborhood
, and open neighborhood  of
of  such that
such that  whenever
whenever  ,
,  ,
, 
Proof.
By (3) and compactness of  , there exists an open neighborhood
, there exists an open neighborhood  of the zero element
of the zero element  of
of  such that
such that  . By (2), there exist open neighborhood
. By (2), there exist open neighborhood  of
of  and open neighborhood
and open neighborhood  of
of  , open neighborhood
, open neighborhood  of
of  such that
such that  whenever
whenever  . Since
. Since  is compact and
is compact and  , there exist finite
, there exist finite  such that
such that  . Taking
. Taking

Clearly,  and
and  are open neighborhood of
are open neighborhood of  and
and  , respectively. Thus for each
, respectively. Thus for each  , we have
, we have  whenever
whenever  ,
,  By (1), there exist open neighborhood
By (1), there exist open neighborhood  of
of  with
with  and open neighborhood
and open neighborhood  of
of  such that
such that  whenever
whenever  , which implies that
, which implies that

whenever  ,
,  ,
, 
The proof is finished.
By Lemma 3.1, we obtain the following result.
Theorem 3.2.
Consider an SGIVQIP  . For each
. For each  , assume that
, assume that
(1) is continuous on
is continuous on  with convex compact values and for each
with convex compact values and for each  ;
;
(2) is upper semicontinuous on
is upper semicontinuous on  with nonempty and compact values;
with nonempty and compact values;
(3) is upper
is upper  semicontinuous on
semicontinuous on  with nonempty and compact values;
with nonempty and compact values;
-
(4)
for each
 and each
and each  ,
, 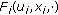 is
is  convex or
convex or  quasiconvex-like;
quasiconvex-like; -
(5)
for each
 and each
and each  , if
, if 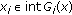 , then
, then 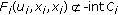 , where
, where 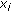 is the
is the  component of
component of  .
.
Then the SGIVQIP has a solution, that is, there exists  such that for each
such that for each  and
and

Proof.
For each  , define a set-valued map
, define a set-valued map  by
by

Step 1.
We prove that the set  is closed. For any sequence
is closed. For any sequence  with
with  , we have
, we have

If  , then there exists
, then there exists  such that for each
such that for each  . By Lemma 3.1, there exist open neighborhood
. By Lemma 3.1, there exist open neighborhood  of
of  and open neighborhood
and open neighborhood  of
of  , such that
, such that  whenever
whenever  . By (1), there exist
. By (1), there exist  such that
such that  , which implies that there exists a positive integer
, which implies that there exists a positive integer  such that
such that  whenever
whenever  . Thus we have
. Thus we have  whenever
whenever  , a contradiction. This shows that
, a contradiction. This shows that  is closed,that is,
is closed,that is,  is open.
is open.
Without loss of generality, assume that  .
.
Define a set-valued map  by
by

Step 2.
We prove that for each  is nonempty and convex.
is nonempty and convex.
For each  , we have
, we have  . By Lemma 3.1, there exists an open neighborhood
. By Lemma 3.1, there exists an open neighborhood  of
of  such that
such that  whenever
whenever  , which implies that
, which implies that  , that is,
, that is,  is open. By (4), it is easy to verify that
is open. By (4), it is easy to verify that  is convex.
is convex.
Since  is convex and
is convex and  , then for each
, then for each  is nonempty and convex.
is nonempty and convex.
Step 3.
We prove that  has a continuous selection
has a continuous selection  .
.
For each  , we have
, we have  and
and  . By
. By  , there exists
, there exists  such that
such that  , where
, where  . Since
. Since  is continuous with convex compact values, then there exists an open neighborhood
is continuous with convex compact values, then there exists an open neighborhood  of
of  such that
such that

whenever  , where
, where  . Thus
. Thus  whenever
whenever  , which implies that
, which implies that  whenever
whenever  , that is,
, that is,  whenever
whenever  . This shows that the set
. This shows that the set  is open. By
is open. By  , we have
, we have  . By Lemma 3.1, there exists an open neighborhood
. By Lemma 3.1, there exists an open neighborhood  of
of  such that
such that

whenever  , which implies that
, which implies that  , that is,
, that is,  is open. Hence, for each
is open. Hence, for each  , the set
, the set  is open.
is open.
By Lemma 2.4,  has a continuous selection
has a continuous selection  .
.
Step 4.
We prove that the SGIVQIP has a solution.
For each  , define the set-valued map
, define the set-valued map  by
by

Note that  is upper semicontinuous when
is upper semicontinuous when  and
and  is upper semicontinuous when
is upper semicontinuous when  , and it is easy to verify that
, and it is easy to verify that  is also upper semicontinuous when
is also upper semicontinuous when  , where
, where  denotes the boundary of
denotes the boundary of  . Thus,
. Thus,  is upper semicontinuous with nonempty convex compact values. By [8, Theorem 7.1.15], the set-valued map
is upper semicontinuous with nonempty convex compact values. By [8, Theorem 7.1.15], the set-valued map  defined by
defined by  is closed with nonempty convex values. By Kakutani-Fan-Glicksberg's fixed points theorem (see [9, pages 550]),
is closed with nonempty convex values. By Kakutani-Fan-Glicksberg's fixed points theorem (see [9, pages 550]),  has a fixed point, that is, there exists
has a fixed point, that is, there exists  . The condition (5) implies that for each
. The condition (5) implies that for each  ,
,  , that is,
, that is,  for each
for each  . Thus we have that for each
. Thus we have that for each  ,
,  and
and

The proof is finished.
If  is a singleton, we obtain the following existence result of solutions to the GIVQIP by Theorem 3.2.
is a singleton, we obtain the following existence result of solutions to the GIVQIP by Theorem 3.2.
Corollary 3.3.
Consider a GIVQIP  . Assume that
. Assume that
(1) is continuous on
is continuous on  with convex compact values and for each
with convex compact values and for each  ;
;
(2) is upper semicontinuous on
is upper semicontinuous on  with nonempty and compact values;
with nonempty and compact values;
(3) is upper
is upper  semicontinuous on
semicontinuous on  with nonempty and compact values;
with nonempty and compact values;
-
(4)
for each
 and each
and each 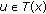 ,
,  is
is 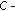 convex or
convex or  quasiconvex-like;
quasiconvex-like; -
(5)
for each
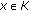 and each
and each  , if
, if 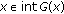 , then
, then  .
.
Then the GIVQIP has a solution, that is, there exists  such that
such that  ,
,

Remark 3.4.
Theorem 3.2, Corollary 3.3, and each corresponding result in literatures [1–6] do not include each other as a special case.
References
Chiang Y, Chadli O, Yao JC: Existence of solutions to implicit vector variational inequalities. Journal of Optimization Theory and Applications 2003,116(2):251–264. 10.1023/A:1022472103162
Cubiotti P, Yao J: Discontinuous implicit generalized quasi-variational inequalities in Banach spaces. Journal of Global Optimization 2007,37(2):263–274. 10.1007/s10898-006-9048-6
Lin L-J, Chen H-L: The study of KKM theorems with applications to vector equilibrium problems with implicit vector variational inequalities problems. Journal of Global Optimization 2005,32(1):135–157. 10.1007/s10898-004-2119-7
Peng J-W, Lee H-WJ, Yang X-M: On system of generalized vector quasi-equilibrium problems with set-valued maps. Journal of Global Optimization 2006,36(1):139–158. 10.1007/s10898-006-9004-5
Ansari QH: Existence of solutions of systems of generalized implicit vector quasi-equilibrium problems. Journal of Mathematical Analysis and Applications 2008,341(2):1271–1283. 10.1016/j.jmaa.2007.11.033
Al-Homidan S, Ansari QH, Schaible S: Existence of solutions of systems of generalized implicit vector variational inequalities. Journal of Optimization Theory and Applications 2007,134(3):515–531. 10.1007/s10957-007-9236-7
Wu X, Shen S: A further generalization of Yannelis-Prabhakar's continuous selection theorem and its applications. Journal of Mathematical Analysis and Applications 1996,197(1):61–74. 10.1006/jmaa.1996.0007
Klein E, Thompson AC: Theory of Correspondences, Canadian Mathematical Society Series of Monographs and Advanced Texts. John Wiley & Sons, New York, NY, USA; 1984:xi+256.
Aliprantis CD, Border KC: Infinite-Dimensional Analysis. 2nd edition. Springer, Berlin, Germany; 1999:xx+672.
Acknowledgments
The research was supported by the Natural Science Foundation of CQ CSTC.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, Z. Existence of Solutions to the System of Generalized Implicit Vector Quasivariational Inequality Problems. J Inequal Appl 2009, 654370 (2009). https://doi.org/10.1155/2009/654370
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/654370
 ,
, 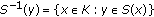 is open.
is open.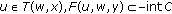 .
. and each
and each  ,
, 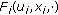 is
is  convex or
convex or  quasiconvex-like;
quasiconvex-like; and each
and each  , if
, if 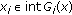 , then
, then 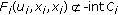 , where
, where 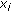 is the
is the  component of
component of  .
. and each
and each 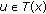 ,
,  is
is 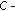 convex or
convex or  quasiconvex-like;
quasiconvex-like;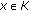 and each
and each  , if
, if 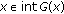 , then
, then  .
.