- Research Article
- Open access
- Published:
On the Identities of Symmetry for the Generalized Bernoulli Polynomials Attached to 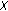 of Higher Order
of Higher Order
Journal of Inequalities and Applications volume 2009, Article number: 640152 (2009)
Abstract
We give some interesting relationships between the power sums and the generalized Bernoulli numbers attached to  of higher order using multivariate
of higher order using multivariate  -adic invariant integral on
-adic invariant integral on  .
.
1. Introduction
Let  be a fixed prime number. Throughout this paper, the symbols
be a fixed prime number. Throughout this paper, the symbols  ,
,  ,
,  , and
, and  denote the ring of rational integers, the ring of
denote the ring of rational integers, the ring of  -adic integers, the field of
-adic integers, the field of  -adic rational numbers, and the completion of algebraic closure of
-adic rational numbers, and the completion of algebraic closure of  , respectively. Let
, respectively. Let  be the set of natural numbers, and
be the set of natural numbers, and  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  with
with  (see [1–24]). Let
(see [1–24]). Let  be the space of uniformly differentiable function on
be the space of uniformly differentiable function on  . Let
. Let  be a fixed positive integer. For
be a fixed positive integer. For  , let
, let

where  lies in
lies in  . For
. For  , the
, the  -adic invariant integral on
-adic invariant integral on  is defined as
is defined as

(see [11–19]). From (1.2), we note that

where  and
and  . Let
. Let  . Then we can derive the following equation from (1.3):
. Then we can derive the following equation from (1.3):

(see [1–11]). Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  . Then the generalized Bernoulli polynomials attached to
. Then the generalized Bernoulli polynomials attached to  are defined as
are defined as

and the generalized Bernoulli numbers attached to  ,
,  , are defined as
, are defined as  (see [1–20, 25]). The purpose of this paper is to derive some identities of symmetry for the generalized Bernoulli polynomials attached to
(see [1–20, 25]). The purpose of this paper is to derive some identities of symmetry for the generalized Bernoulli polynomials attached to  of higher order.
of higher order.
2. Symmetric Properties for the Generalized Bernoulli Polynomials of Higher Order
Let  be the Dirichlet's character with conductor
be the Dirichlet's character with conductor  . Then we note that
. Then we note that

where  are the
are the  th generalized Bernoulli numbers attached to
th generalized Bernoulli numbers attached to  (see [7, 9, 15, 25]). Now we also see that the generalized Bernoulli polynomials attached to
(see [7, 9, 15, 25]). Now we also see that the generalized Bernoulli polynomials attached to  are given by
are given by

By (2.1) and (2.2), we have


(see [1–19, 25]). For  , we obtain that
, we obtain that

where  . Thus, we have
. Thus, we have

Then

Let us define the  -adic function
-adic function  as follows:
as follows:

(see [25]). By (2.7) and (2.8), we see that

(see [25]). Thus, we have

This means that

(see [25]).
The generalized Bernoulli polynomials attached to  of order
of order  , which is denoted by
, which is denoted by  , are defined as
, are defined as

Then the values of  at
at  are called the generalized Bernoulli numbers attached to
are called the generalized Bernoulli numbers attached to  of order
of order  . When
. When  , the polynomials of numbers are called the generalized Bernoulli polynomials or numbers attached to
, the polynomials of numbers are called the generalized Bernoulli polynomials or numbers attached to  . Let
. Let  . Then we set
. Then we set

where

In (2.13), we note that  is symmetric in
is symmetric in  . From (2.13), we derive
. From (2.13), we derive

It is easy to see that

From (2.16), we note that

By the symmetry of  in
in  and
and  , we see that
, we see that

By comparing the coefficients on the both sides of (2.17) and (2.18), we see the following theorem.
Theorem 2.1.
For  , one has
, one has

Remark 2.2.
Let  and
and  in (1.4). Then we have
in (1.4). Then we have

(see [25]).
We also calculate that

From the symmetric property of  in
in  and
and  , we derive
, we derive

By comparing the coefficients on the both sides of (2.21) and (2.22), we obtain the following theorem.
Theorem 2.3.
For  , one has
, one has

Remark 2.4.
Let  and
and  in (2.23). We have
in (2.23). We have

(see [25]).
References
Cenkci M: The
 -adic generalized twisted
-adic generalized twisted 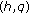 -Euler-
-Euler- -function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37–47.
-function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37–47.Cenkci M, Simsek Y, Kurt V: Multiple two-variable
 -adic
-adic 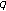 -
-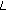 -function and its behavior at
-function and its behavior at 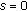 . Russian Journal of Mathematical Physics 2008,15(4):447–459. 10.1134/S106192080804002X
. Russian Journal of Mathematical Physics 2008,15(4):447–459. 10.1134/S106192080804002XJang L-C, Kim S-D, Park D-W, Ro Y-S: A note on Euler number and polynomials. Journal of Inequalities and Applications 2006, 2006:-5.
Kim T:
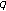 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.Kim T: A note on
 -Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005,8(1):13–17.
-Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005,8(1):13–17.Kim T:
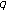 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 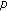 -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3Kim T: A note on
 -adic
-adic 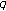 -integral on
-integral on 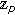 associated with
associated with 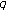 -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137.Kim T: On the
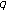 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037Kim T: On
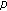 -adic
-adic 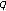 -
- -functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071
-functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071Kim T: On the multiple
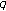 -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481–486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481–486. 10.1134/S1061920808040055Kim T: New approach to
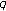 -Euler, Genocchi numbers and their interpolation functions. Advanced Studies in Contemporary Mathematics 2009,18(2):105–112.
-Euler, Genocchi numbers and their interpolation functions. Advanced Studies in Contemporary Mathematics 2009,18(2):105–112.Kim T: On a
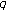 -analogue of the
-analogue of the 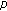 -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373Kim T: Sums of products of -Euler numbers. to appear in Journal of Computational Analysis and Applications to appear in Journal of Computational Analysis and Applications
Kim T, Choi JY, Sug JY: Extended
 -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic  -adic
-adic 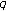 -integral on
-integral on 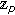 . Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045
. Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045Kim T:
 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288–299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288–299.Kim Y-H, Kim W, Jang L-C: On the
 -extension of Apostol-Euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10.
-extension of Apostol-Euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10.Pečarić J, Vukelić A: General dual Euler-Simpson formulae. Journal of Mathematical Inequalities 2008,2(4):511–526.
Simsek Y: Complete sum of products of -extension of the Euler polynomials and numbers. http://arxiv.org/abs/0707.2849
Simsek Y: On
 -adic twisted
-adic twisted  -
- - functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095
- functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095Simsek Y, Kurt V, Kim D: New approach to the complete sum of products of the twisted
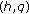 -Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44–56. 10.2991/jnmp.2007.14.1.5
-Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44–56. 10.2991/jnmp.2007.14.1.5Kim T: Symmetry properties of higher order Bernoulli polynomials. (communicated) (communicated)
Zhang Z, Yang H: Some closed formulas for generalized Bernoulli-Euler numbers and polynomials. Proceedings of the Jangjeon Mathematical Society 2008,11(2):191–198.
Tekcan A, Özkoç A, Gezer B, Bizim O: Some relations involving the sums of Fibonacci numbers. Proceedings of the Jangjeon Mathematical Society 2008,11(1):1–12.
Khrennikov AYu: Generalized probabilities taking values in non-Archimedean fields and in topological groups. Russian Journal of Mathematical Physics 2007,14(2):142–159. 10.1134/S1061920807020033
Kim T, Rim S-H, Lee B: Some identities of symmetry for the generalized Bernoulli numbers and polynomials. Abstract and Applied Analysis 2009, 2009:-8.
Acknowledgment
The present research has been conducted by the research Grant of the Kwangwoon University in 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, T., Jang, LC., Kim, YH. et al. On the Identities of Symmetry for the Generalized Bernoulli Polynomials Attached to 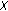 of Higher Order.
J Inequal Appl 2009, 640152 (2009). https://doi.org/10.1155/2009/640152
of Higher Order.
J Inequal Appl 2009, 640152 (2009). https://doi.org/10.1155/2009/640152
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/640152
 -adic generalized twisted
-adic generalized twisted 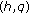 -Euler-
-Euler- -function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37–47.
-function and its applications. Advanced Studies in Contemporary Mathematics 2007,15(1):37–47. -adic
-adic 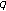 -
-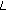 -function and its behavior at
-function and its behavior at 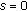 . Russian Journal of Mathematical Physics 2008,15(4):447–459. 10.1134/S106192080804002X
. Russian Journal of Mathematical Physics 2008,15(4):447–459. 10.1134/S106192080804002X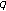 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51–57. -Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005,8(1):13–17.
-Volkenborn integration. Proceedings of the Jangjeon Mathematical Society 2005,8(1):13–17.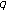 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with 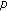 -adic
-adic  -integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3
-integrals. Journal of Nonlinear Mathematical Physics 2007,14(1):15–27. 10.2991/jnmp.2007.14.1.3 -adic
-adic 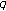 -integral on
-integral on 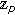 associated with
associated with 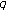 -Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137.
-Euler numbers. Advanced Studies in Contemporary Mathematics 2007,15(2):133–137.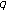 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458–1465. 10.1016/j.jmaa.2006.03.037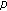 -adic
-adic 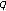 -
- -functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071
-functions and sums of powers. Journal of Mathematical Analysis and Applications 2007,329(2):1472–1481. 10.1016/j.jmaa.2006.07.071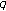 -Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481–486. 10.1134/S1061920808040055
-Genocchi and Euler numbers. Russian Journal of Mathematical Physics 2008,15(4):481–486. 10.1134/S1061920808040055 -Euler, Genocchi numbers and their interpolation functions. Advanced Studies in Contemporary Mathematics 2009,18(2):105–112.
-Euler, Genocchi numbers and their interpolation functions. Advanced Studies in Contemporary Mathematics 2009,18(2):105–112. -analogue of the
-analogue of the  -adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373
-adic log gamma functions and related integrals. Journal of Number Theory 1999,76(2):320–329. 10.1006/jnth.1999.2373 -Euler numbers and polynomials associated with fermionic
-Euler numbers and polynomials associated with fermionic  -adic
-adic  -integral on
-integral on  . Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045
. Russian Journal of Mathematical Physics 2007,14(2):160–163. 10.1134/S1061920807020045
 -extension of Apostol-Euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10.
-extension of Apostol-Euler numbers and polynomials. Abstract and Applied Analysis 2008, 2008:-10. -adic twisted
-adic twisted  -
- - functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095
- functions related to generalized twisted Bernoulli numbers. Russian Journal of Mathematical Physics 2006,13(3):340–348. 10.1134/S1061920806030095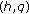 -Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44–56. 10.2991/jnmp.2007.14.1.5
-Bernoulli numbers and polynomials. Journal of Nonlinear Mathematical Physics 2007,14(1):44–56. 10.2991/jnmp.2007.14.1.5