- Research Article
- Open access
- Published:
Generalized 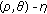 Invariant Monotonicity and Generalized
Invariant Monotonicity and Generalized  Invexity of Nondifferentiable Functions
Invexity of Nondifferentiable Functions
Journal of Inequalities and Applications volume 2009, Article number: 393940 (2009)
Abstract
New concepts of generalized  invex functions for non-differentiable functions and generalized
invex functions for non-differentiable functions and generalized  invariant monotone operators for set-valued mappings are introduced. The relationships between generalized
invariant monotone operators for set-valued mappings are introduced. The relationships between generalized  invexity of functions and generalized
invexity of functions and generalized  invariant monotonicity of the corresponding Clarke's subdifferentials are studied. Some of our results are extension and improvement of some results obtained in (Jabarootion and Zafarani (2006); Behera et al. (2008)).
invariant monotonicity of the corresponding Clarke's subdifferentials are studied. Some of our results are extension and improvement of some results obtained in (Jabarootion and Zafarani (2006); Behera et al. (2008)).
1. Introduction
Convexity plays a central role in mathematical economics, engineering, management sciences, and optimization. In recent years several extensions and generalizations have been developed for classical convexity. An important generalization of convex functions is invex functions introduced by Hanson (1981) [1]. He has shown that the Kuhn-Tuker conditions are sufficient for optimality of nonlinear programming problems under invexity conditions. Kaul and Kaur (1985) [2] presented the conpects of pseudoinvex and quasi-invex functions and investigated their applications in nonlinear programming. A concept closely related to the convexity of function is the monotonicity of function; it is worth noting that monotonicity plays a very important role in the study of the existence and sensitivity analysis of solutions for variational inequality problems. An important breakthrough was given by Karamardian and Schaible (1990) [3]. They have proved that the generalized convexity of the function  is equivalent to the generalized monotonicity of its gradient function
is equivalent to the generalized monotonicity of its gradient function  . Motivated by the work of Karamardian and Schaible (1990), there has been increasing interest in the study of monotonicity and generalized monotonicity and their relationships to convexity and generalized convexity. Ruiz-Garzón et al. (2003) [4] introduced strongly invex and strongly pseudoinvex functions in
. Motivated by the work of Karamardian and Schaible (1990), there has been increasing interest in the study of monotonicity and generalized monotonicity and their relationships to convexity and generalized convexity. Ruiz-Garzón et al. (2003) [4] introduced strongly invex and strongly pseudoinvex functions in  and gave the sufficient conditions for (strictly, strongly) invex monotonicity, strictly pseudoinvex monotonicity, and quasi-invex monotonicity. Moreover, in [4] the necessary conditions for strictly pseudoinvex monotonicity and pseudoinvex monotonicity were obtained. The necessary conditions for strongly pseudoinvex monotonicity were given by Yang et al. (2005) [5]. The results on generalized invexity and generalized invex monotonicity obtained in [4–6] are studied in
and gave the sufficient conditions for (strictly, strongly) invex monotonicity, strictly pseudoinvex monotonicity, and quasi-invex monotonicity. Moreover, in [4] the necessary conditions for strictly pseudoinvex monotonicity and pseudoinvex monotonicity were obtained. The necessary conditions for strongly pseudoinvex monotonicity were given by Yang et al. (2005) [5]. The results on generalized invexity and generalized invex monotonicity obtained in [4–6] are studied in  -dimensional Euclidean space. Several generalizations in real Banach space have been developed for generalized invexity and generalized invex monotonicity. Recently, Fan et al. (2003) [7] have studied the relationships between (strict, strong) convexity, pseudoconvexity, and quasiconvexity of functions and (strict, strong) monotonicity, pseudomonotonicity, and quasimonotonicity of its Clarke's generalized subdifferential mapping, respectively. Jabarootian and Zafarani (2006) [8] generalized convexity to invexity and obtained the relationships between several kinds of generalized invexity of functions and generalized invariant monotonicity of its Clarke's generalized subdifferential mapping.
-dimensional Euclidean space. Several generalizations in real Banach space have been developed for generalized invexity and generalized invex monotonicity. Recently, Fan et al. (2003) [7] have studied the relationships between (strict, strong) convexity, pseudoconvexity, and quasiconvexity of functions and (strict, strong) monotonicity, pseudomonotonicity, and quasimonotonicity of its Clarke's generalized subdifferential mapping, respectively. Jabarootian and Zafarani (2006) [8] generalized convexity to invexity and obtained the relationships between several kinds of generalized invexity of functions and generalized invariant monotonicity of its Clarke's generalized subdifferential mapping.
Behera et al. (2008) [9] introduce the concepts of generalized  invariant monotone operators and generalized
invariant monotone operators and generalized  invex functions and discuss the relationships between generalized
invex functions and discuss the relationships between generalized  invariant monotonicity and generalized
invariant monotonicity and generalized  invexity. Some examples are presented by Behera et al. to illustrate the proper generalizations for the corresponding concepts of generalized invariant monotone. However, it is noted that the definition of strictly
invexity. Some examples are presented by Behera et al. to illustrate the proper generalizations for the corresponding concepts of generalized invariant monotone. However, it is noted that the definition of strictly  quasi-invex is not defined precisely in [9], and Theorem 3.2 of [9] contains some errors. The purpose of this paper is to point out these errors and to suggest appropriate modifications. In real Banach space, we define new concepts of generalized
quasi-invex is not defined precisely in [9], and Theorem 3.2 of [9] contains some errors. The purpose of this paper is to point out these errors and to suggest appropriate modifications. In real Banach space, we define new concepts of generalized  invexity for non-differentiable functions and generalized
invexity for non-differentiable functions and generalized  invariant monotonicity for set-valued mappings which are extension and improvement of the corresponding definitions of [8, 9]. In [9], some sufficient conditions for generalized
invariant monotonicity for set-valued mappings which are extension and improvement of the corresponding definitions of [8, 9]. In [9], some sufficient conditions for generalized  invariant pseudomonotonicity and generalized
invariant pseudomonotonicity and generalized  invariant quasimonotonicity were given. We will give some necessary conditions. We also introduce the concept of strongly
invariant quasimonotonicity were given. We will give some necessary conditions. We also introduce the concept of strongly  invariant pseudomonotone and give its necessary conditions. Some results that obtained in this paper are the improvement of the corresponding results of [8, 9].
invariant pseudomonotone and give its necessary conditions. Some results that obtained in this paper are the improvement of the corresponding results of [8, 9].
2. Preliminaries
In this paper, let  be a real Banach space endowed with a norm
be a real Banach space endowed with a norm  and
and  its dual space with a norm
its dual space with a norm  . We denote by
. We denote by  ,
,  ,
,  , and
, and  the family of all nonempty subsets of
the family of all nonempty subsets of  , the dual pair between
, the dual pair between  and
and  , the line segment for
, the line segment for  , and the interior of
, and the interior of  , respectively. Let
, respectively. Let  be a nonempty open subset of
be a nonempty open subset of  ,
,  a set-valued mapping,
a set-valued mapping,  a vector-valued function, and
a vector-valued function, and  a non-differentiable real-valued function. The following concepts and results are taken from [10].
a non-differentiable real-valued function. The following concepts and results are taken from [10].
Definition 2.1.
Let  be locally Lipschitz continuous at a given point
be locally Lipschitz continuous at a given point  and
and  any vector in
any vector in  . The Clarke's generalized directional derivative of
. The Clarke's generalized directional derivative of  at
at  in the direction
in the direction  , denoted by
, denoted by  , is defined by
, is defined by

Definition 2.2.
Let  be locally Lipschitz continuous at a given point
be locally Lipschitz continuous at a given point  and let
and let  be any vector in
be any vector in  . The Clarke's generalized subdifferential of
. The Clarke's generalized subdifferential of  at
at  , denoted by
, denoted by  , is defined as follows:
, is defined as follows:

Lemma 2.3 (Mean Value Theorem).
Let  and
and  be point in
be point in  and suppose that
and suppose that  is Lipschitz near each point of a nonempty closed convex set containing the line segment
is Lipschitz near each point of a nonempty closed convex set containing the line segment  . Then there exists a point
. Then there exists a point  such that
such that

3.  Invariant Monotonicity and
Invariant Monotonicity and  Invexity
Invexity
Let  be nonempty subset of
be nonempty subset of  and let
and let  and
and  be two vector-valued functions from
be two vector-valued functions from  to
to  and
and 
Definition 3.1.
Let  be nonempty subset of
be nonempty subset of  and let
and let  be a set-valued mapping:
be a set-valued mapping:
(1) is said to be
is said to be  invariant monotone on
invariant monotone on  with respect to
with respect to  and
and  if for any
if for any  and any
and any  ,
,  , one has
, one has

(2) is said to be strictly
is said to be strictly  invariant monotone on
invariant monotone on  with respect to
with respect to  and
and  if for any
if for any  with
with  and any
and any  ,
,  , one has
, one has

Remark 3.2.
-
(1)
When
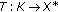 , it is [9, Definition 2.3].
, it is [9, Definition 2.3].
(2)When  , every (strictly)
, every (strictly)  invariant monotone function is a (strictly) invariant monotone function defined by Jabarootian and Zafarani [8], but the converse is not true. Examples 2.1 and 2.2 of [9] are two counterexamples, where
invariant monotone function is a (strictly) invariant monotone function defined by Jabarootian and Zafarani [8], but the converse is not true. Examples 2.1 and 2.2 of [9] are two counterexamples, where  is defined as
is defined as  .
.
(3)When  ,
,  , Definition 3.1(1) is the Definition 3.2(3) in [8], that is, strongly invariant monotone.
, Definition 3.1(1) is the Definition 3.2(3) in [8], that is, strongly invariant monotone.
Next we introduce  invex functions under non-differentiable condition.
invex functions under non-differentiable condition.
Definition 3.3.
Let  be nonempty subset of
be nonempty subset of  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Then,
. Then,
(1)the function  is said to be
is said to be  invex with respect to
invex with respect to  and
and  on
on  if for any
if for any  and any
and any  , one has
, one has

(2)the function  is said to be strictly
is said to be strictly  invex with respect to
invex with respect to  and
and  on
on  if for any
if for any  with
with  and any
and any  , one has
, one has

The following lemma under non-differentiable condition is similar to Lemmas 2.3 and 2.4 under Fréchet differentiable condition in [9].
Lemma 3.4.
Let  be locally Lipschitz on
be locally Lipschitz on  . If
. If  is (strictly)
is (strictly)  invex with respect to
invex with respect to  and
and  on
on  , then
, then  is (strictly)
is (strictly)  invariant monotone with respect to the same
invariant monotone with respect to the same  and
and  on
on  .
.
4.  Invariant Quasimonotonicity and
Invariant Quasimonotonicity and 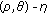 Quasi-Invexity
Quasi-Invexity
In this section, we will point out some errors in [9].
Definition 4.1 (see [11]).
A set  is said to be invex with respect to
is said to be invex with respect to  if there exists an
if there exists an  such that, for any
such that, for any  and
and  ,
,

Definition 4.2 (see [9, Definition 3.2]).
A Fréchet differentiable function  is said to be
is said to be  quasi-invex with respect to
quasi-invex with respect to  and
and  on
on  if for any
if for any  with
with  , we have
, we have

If strict inequality holds, then it is said to be strictly  quasi-invex, where
quasi-invex, where  is the Fréchet differential of
is the Fréchet differential of  .
.
Definition 4.3 (see [9, Definition 4.2]).
A Fréchet differentiable function  is said to be
is said to be  pseudoinvex with respect to
pseudoinvex with respect to  and
and  on
on  if for any
if for any  with
with  , we have
, we have

Definition 4.4 (see [9, Definition 5.2]).
A Fréchet differentiable function  is said to be strictly
is said to be strictly  pseudoinvex with respect to
pseudoinvex with respect to  and
and  on
on  if for any
if for any  with
with  , we have
, we have

Remark 4.5.
In Definition 4.2, the definition of strictly  quasi-invex is not defined precisely, as can be seen below. If it holds that
quasi-invex is not defined precisely, as can be seen below. If it holds that

then, by Definition 4.3,  is
is  pseudoinvex function with respect to
pseudoinvex function with respect to  and
and  on
on  . On the other hand, if the following is OK:
. On the other hand, if the following is OK:

then, by Definition 4.4,  is strictly
is strictly  pseudoinvex function with respect to
pseudoinvex function with respect to  and
and  on
on  .
.
Thus, we must conclude that the following implication holds

that is, the "strict inequality" for strictly  quasi-invex functions in Definition 4.2 means (4.7).
quasi-invex functions in Definition 4.2 means (4.7).
Definition 4.6 (see [9, Definition 3.1]).
A function  is said to be
is said to be  invariant quasimonotone (strictly) with respect to
invariant quasimonotone (strictly) with respect to  and
and  on
on  if for any
if for any  with
with  , we have
, we have

Definition 4.7 (see [9, Definition 4.1]).
A function  is said to be
is said to be  invariant pseudomonotone with respect to
invariant pseudomonotone with respect to  and
and  on
on  if for any
if for any  ,we have
,we have

The following Theorem is due to Behera et al. in [9].
Theorem 4 (see [9, Theorem 3.2]).
Let  be an invex set with respect to
be an invex set with respect to  , and let
, and let  be Fréchet differentiable on
be Fréchet differentiable on  . If
. If  is strictly
is strictly  quasi-invex with respect to
quasi-invex with respect to  and
and  on
on  , then
, then  is a strictly
is a strictly  invariant quasimonotone function with respect to the same
invariant quasimonotone function with respect to the same  and
and  on
on  .
.
Remark 4.8.
By Remark 4.5, Theorem A is not true as can be seen from the following example.
Example 4.9.
Let  ,
,  , and
, and  be functions defined by
be functions defined by

Take  .
.
When  , we have
, we have

Then,  Clearly, by (4.7),
Clearly, by (4.7),  is strictly
is strictly  quasi-invex with respect to
quasi-invex with respect to  and
and  on
on  , but
, but

Thus,  is not strictly
is not strictly  invariant quasimonotone.
invariant quasimonotone.
On the other hand, when  ,
,

but

Thus,  is not
is not  invariant pseudomonotone.
invariant pseudomonotone.
Furthermore,  is
is  invariant quasimonotone. Hence, Example 4.9 also illustrates that
invariant quasimonotone. Hence, Example 4.9 also illustrates that  invariant quasimonotone is not necessarily strictly
invariant quasimonotone is not necessarily strictly  invariant quasimonotone or
invariant quasimonotone or  invariant pseudomonotone.
invariant pseudomonotone.
In [9], sufficient conditions for  invariant quasimonotone for Fréchet differentiable functions were given. However, necessary conditions have been missing. In what follows, we will give the necessary conditions for
invariant quasimonotone for Fréchet differentiable functions were given. However, necessary conditions have been missing. In what follows, we will give the necessary conditions for  invariant quasimonotonity and study the relationship between
invariant quasimonotonity and study the relationship between  invariant quasimonotonicity and
invariant quasimonotonicity and  quasi-invexity.
quasi-invexity.
Definition 4.10.
Let  be a nonempty subset of
be a nonempty subset of  and
and  is said to be
is said to be  invariant quasimonotone on
invariant quasimonotone on  with respect to
with respect to  and
and  if for any
if for any  and any
and any  ,
,  , one has
, one has

Remark 4.11.
When  , every
, every  invariant quasimonotone function is an invariant quasimonotone function defined by Jabarootian and Zafarani [8], but the converse is not true. See [9, Example 3.1], for a counterexample, where
invariant quasimonotone function is an invariant quasimonotone function defined by Jabarootian and Zafarani [8], but the converse is not true. See [9, Example 3.1], for a counterexample, where

Definition 4.12.
Let  be a nonempty subset of
be a nonempty subset of  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Then, the function
. Then, the function  is said to be
is said to be  quasi-invex with respect to
quasi-invex with respect to  and
and  on
on  if for any
if for any  and any
and any  , one has
, one has

The following theorem under non-differentiable condition is similar to Theorem 3.1 of Behera et al. in [9].
Theorem 4.13.
Let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . If
. If  is
is  quasi-invex with respect to
quasi-invex with respect to  and
and  on
on  , then
, then  is a
is a  invariant quasimonotone mapping with respect to the same
invariant quasimonotone mapping with respect to the same  and
and  on
on  .
.
Proof.
Suppose  is
is  quasi-invex with respect to
quasi-invex with respect to  and
and  on
on  . Let
. Let  ,
,  , and
, and  be such that
be such that

By  quasi-invexity of
quasi-invexity of  , we have
, we have

Note that  quasi-invexity of
quasi-invexity of  implies
implies

Therefore,  is a
is a  invariant quasimonotone mapping with respect to the same
invariant quasimonotone mapping with respect to the same  and
and  on
on  .
.
Condition C (see [12]).
Let  Then, for any
Then, for any  and for any
and for any  ,
,

Definition 4.14 (see [4]).
A function  is said to be a skew function if
is said to be a skew function if  for all
for all 
Now we will give the sufficient conditions for  quasi-invexity.
quasi-invexity.
Theorem 4.15.
Let  be an open invex set with respect to
be an open invex set with respect to  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Suppose that
. Suppose that
(1) is a
is a  invariant quasimonotone mapping with respect to
invariant quasimonotone mapping with respect to  and
and  on
on  ;
;
(2) satisfies Condition C;
satisfies Condition C;
(3)for each  and
and  , there exist
, there exist  and
and  , such that
, such that

(4)
Then,  is a
is a  quasi-invex function with respect to the same
quasi-invex function with respect to the same  and
and  on
on  .
.
Proof.
Suppose that  is not a
is not a  quasi-invex function with respect to
quasi-invex function with respect to  and
and  on
on  . Then, there exist
. Then, there exist  and
and  , such that
, such that

but

By hypothesis 3 and (4.23), there exist  ,
,  such that
such that

It follows from Condition C, (4.25), and hypothesis 4 that

Since  is a
is a  invariant quasimonotone mapping with respect to
invariant quasimonotone mapping with respect to  and
and  on
on  , (4.26) implies
, (4.26) implies

From Condition C, hypothesis 4, and (4.27), we obtain

which contradicts (4.24). Hence,  is a
is a  quasi-invex function with respect to the same
quasi-invex function with respect to the same  and
and  on
on  .
.
Similar to proof for Theorem 4.15, we can obtain the following theorem.
Theorem 4.16.
Let  be an open convex subset of
be an open convex subset of  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Suppose that
. Suppose that
(1) is a
is a  invariant quasimonotone mapping with respect to
invariant quasimonotone mapping with respect to  and
and  on
on  ;
;
(2) and
and  are affine in the first argument and skew;
are affine in the first argument and skew;
(3)for each  and
and  , there exist
, there exist  ,
,  , where
, where  , such that
, such that

Then,  is a
is a  quasi-invex function with respect to the same
quasi-invex function with respect to the same  and
and  on
on  .
.
5. 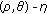 Invariant Pseudomonotonicity and
Invariant Pseudomonotonicity and 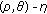 Pseudoinvexity
Pseudoinvexity
Definition 5.1.
Let  be a nonempty subset of
be a nonempty subset of  , and let
, and let  be a set-valued mapping. Then,
be a set-valued mapping. Then,
(1) is said to be
is said to be  invariant pseudomonotone on
invariant pseudomonotone on  with respect to
with respect to  and
and  if for any
if for any  and any
and any  ,
,  , one has
, one has

(2) is said to be strictly
is said to be strictly  invariant pseudomonotone on
invariant pseudomonotone on  with respect to
with respect to  and
and  if for any
if for any  with
with  and any
and any  ,
,  , one has
, one has

Remark 5.2.
When  , every (strictly)
, every (strictly)  invariant pseudomonotone function is (strictly) invariant pseudomonotone function [8] on
invariant pseudomonotone function is (strictly) invariant pseudomonotone function [8] on  with respect to the same
with respect to the same  , but the converse is not ture. Examples 4.1 and 5.1 of [9] are two counterexamples, where
, but the converse is not ture. Examples 4.1 and 5.1 of [9] are two counterexamples, where  is defined as
is defined as  .
.
Definition 5.3.
Let  be a nonempty subset of
be a nonempty subset of  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Then,
. Then,
(1)the function  is said to be
is said to be  pseudoinvex with respect to
pseudoinvex with respect to  and
and  on
on  if for any
if for any  and any
and any  , one has
, one has

(2)the function  is said to be strictly
is said to be strictly  pseudoinvex with respect to
pseudoinvex with respect to  and
and  on
on  if for any
if for any  with
with  and any
and any  , one has
, one has

In this section we will give sufficient conditions and necessary conditions for  invariant pseudomonotonicity.
invariant pseudomonotonicity.
Theorem 5.4.
Let  be an open invex set with respect to
be an open invex set with respect to  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Suppose that
. Suppose that
(1) is a
is a  pseudoinvex function with respect to
pseudoinvex function with respect to  and
and  on
on  ;
;
(2) satisfies Condition C;
satisfies Condition C;
(3)for any  and
and  , there exists
, there exists  such that
such that  ;
;
(4)
Then,  is a
is a  invariant pseudomonotone mapping with respect to the same
invariant pseudomonotone mapping with respect to the same  and
and  on
on  .
.
Proof.
Suppose that  is a
is a  pseudoinvex function with respect to
pseudoinvex function with respect to  and
and  on
on  . Let
. Let  . If
. If  ,
,

We need to show

Suppose, on the contrary,  , such that
, such that

Since  is a
is a  pseudoinvex function with respect to
pseudoinvex function with respect to  and
and  on
on  , (5.7) implies
, (5.7) implies

From hypothesis 3 and (5.8),  such that
such that

Hence,  pseudoinvexity of
pseudoinvexity of  implies
implies

From Condition C, hypothesis 4, and (5.10), we have

which contradicts (5.5). Hence,  is a
is a  invariant pseudomonotone mapping with respect to the same
invariant pseudomonotone mapping with respect to the same  and
and  on
on  .
.
Corollary 5.5.
Let  be an open invex set with respect to
be an open invex set with respect to  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  , and let
, and let  satisfy Condition C. If, for any
satisfy Condition C. If, for any 
(1) such that
such that  ;
;
(2) is a pseudoinvex function with respect to
is a pseudoinvex function with respect to  on
on  ,
,
then,  is an invariant pseudomonotone mapping with respect to the same
is an invariant pseudomonotone mapping with respect to the same  on
on  .
.
Theorem 5.6.
Let  be an open invex set with respect to
be an open invex set with respect to  and let
and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Suppose that
. Suppose that
(1) is a
is a  invariant pseudomonotone mapping with respect to
invariant pseudomonotone mapping with respect to  and
and  on
on  ;
;
(2) satisfies Condition C;
satisfies Condition C;
(3)for any  and
and  , there exist
, there exist  ,
,  , such that
, such that

(4)
Then,  is a
is a  pseudoinvex function with respect to the same
pseudoinvex function with respect to the same  and
and  on
on  .
.
Proof.
Suppose that  is a
is a  invariant pseudomonotone mapping with respect to
invariant pseudomonotone mapping with respect to  and
and  on
on  . Let
. Let  for all
for all  be such that
be such that

We need to show

Assume, on the contrary,

By hypothesis 3,  such that
such that

From Condition C, hypothesis 4, and (5.16), we have

Since  is an invariant pseudomonotone mapping with respect to
is an invariant pseudomonotone mapping with respect to  and
and  , (5.17) implies
, (5.17) implies

From Condition C, hypothesis 4, and (5.18), we obtain

which contradicts (5.13). Hence,  is a
is a  pseudoinvex function with respect to the same
pseudoinvex function with respect to the same  and
and  on
on  .
.
Corollary 5.7.
Let  be an open invex set with respect to
be an open invex set with respect to  , let
, let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  , and let
, and let  satisfy Condition C. For any
satisfy Condition C. For any  ,
,  such that
such that

If  is an invariant pseudomonotone mapping with respect to
is an invariant pseudomonotone mapping with respect to  on
on  , then
, then  is a pseudoinvex function with respect to the same
is a pseudoinvex function with respect to the same  on
on  .
.
Similar to proof for Theorems 5.4 and 5.6, we can obtain the following two theorems.
Theorem 5.8.
Let  be an open convex subset of
be an open convex subset of  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Suppose that
. Suppose that
(1) is a
is a  pseudoinvex function with respect to
pseudoinvex function with respect to  and
and  on
on  ;
;
(2) and
and  are affine in the first argument and skew;
are affine in the first argument and skew;
(3)for any  and
and  , there exists
, there exists  such that
such that

Then,  is a
is a  invariant pseudomonotone mapping with respect to the same
invariant pseudomonotone mapping with respect to the same  and
and  on
on  .
.
Theorem 5.9.
Let  be an open convex subset of
be an open convex subset of  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Suppose that
. Suppose that
(1) is a
is a  invariant pseudomonotone mapping with respect to
invariant pseudomonotone mapping with respect to  and
and  on
on  ;
;
(2) and
and  are affine in the first argument and skew;
are affine in the first argument and skew;
(3)for each  and
and  , there exist
, there exist  ,
,  , where
, where  such that
such that

Then,  is a
is a  pseudoinvex function with respect to the same
pseudoinvex function with respect to the same  and
and  on
on  .
.
6. Strongly 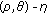 Invariant Pseudomonotonicity and Strongly
Invariant Pseudomonotonicity and Strongly 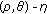 Pseudoinvexity
Pseudoinvexity
In this section, we introduce the concepts of strongly  invariant pseudomonotonicity and strongly
invariant pseudomonotonicity and strongly  pseudoinvexity. We will give a necessary condition for strongly
pseudoinvexity. We will give a necessary condition for strongly  invariant pseudomonotonicity.
invariant pseudomonotonicity.
Definition 6.1.
Let  be a nonempty subset of
be a nonempty subset of  . Then,
. Then,  is said to be strongly
is said to be strongly  invariant pseudomonotone on
invariant pseudomonotone on  with respect to
with respect to  and
and  if there exists a constant
if there exists a constant  , such that for any
, such that for any  and any
and any  ,
,  , one has
, one has

Definition 6.2.
Let  be a nonempty subset of
be a nonempty subset of  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Then, the function
. Then, the function  is said to be strongly
is said to be strongly  pseudoinvex with respect to
pseudoinvex with respect to  and
and  on
on  , if there exists a constant
, if there exists a constant  , such that for any
, such that for any  and any
and any  , one has
, one has

Theorem 6.3.
Let  be an open invex set with respect to
be an open invex set with respect to  , and let
, and let  be locally Lipschitz continuous on
be locally Lipschitz continuous on  . Suppose that
. Suppose that
(1) is a strongly
is a strongly  invariant pseudomonotone with respect to
invariant pseudomonotone with respect to  and
and  on
on  ;
;
(2) satisfies Condition C;
satisfies Condition C;
(3) , for any
, for any  ;
;
(4)
Then,  is a strongly
is a strongly  pseudoinvex function with respect to the same
pseudoinvex function with respect to the same  and
and  on
on  .
.
Proof.
Suppose that  is strongly
is strongly  invariant pseudomonotone with respect to
invariant pseudomonotone with respect to  and
and  on
on  . Let
. Let  and for all
and for all  be such that
be such that

Let  . By the Mean Value Theorem, there exist
. By the Mean Value Theorem, there exist  and
and  where
where  , such that
, such that

Hence, by Condition C, we have

and there exists  , where
, where  , such that
, such that

Thus, by Condition C, we have

On the other hand, it follows from hypothesis 4, Condition C, and (6.3) that

By strongly  invariant pseudomonotonicity of
invariant pseudomonotonicity of  , we obtain
, we obtain


Then, by (6.5), (6.9), and hypothesis 4, we have

Furthermore, by (6.7), (6.10), and hypothesis 4, we obtain

Adding inequalities (6.11) and (6.12), we have

By hypothesis 3, it is clear that

Thus,  is a strongly
is a strongly  pseudoinvex function with respect to the same
pseudoinvex function with respect to the same  and
and  on
on  .
.
7. Conclusions
In this paper, we introduced various concepts of generalized  invariant monotonicity and established their relations with generalized
invariant monotonicity and established their relations with generalized  invexity. Diagram (7.1) summarizes these relations, where
invexity. Diagram (7.1) summarizes these relations, where  means that the implication relation holds and
means that the implication relation holds and  means that the implication relation does not hold:
means that the implication relation does not hold:

where IM stands for invariant monotonicity, IPM stands for invariant pseudomonotonicity, and IQM stands for invariant quasimonotonicity.
For the generalized  invexity of a real-valued function, the relations in Diagram (7.2) hold:
invexity of a real-valued function, the relations in Diagram (7.2) hold:

Under certain conditions, we obtain the relationships between generalized  invexity in Diagram (7.2) and the corresponding generalized
invexity in Diagram (7.2) and the corresponding generalized  invariant monotonicity in Diagram (7.1).
invariant monotonicity in Diagram (7.1).
References
Hanson MA: On sufficiency of the Kuhn-Tucker conditions. Journal of Mathematical Analysis and Applications 1981,80(2):545–550. 10.1016/0022-247X(81)90123-2
Kaul RN, Kaur S: Optimality criteria in nonlinear programming involving nonconvex functions. Journal of Mathematical Analysis and Applications 1985,105(1):104–112. 10.1016/0022-247X(85)90099-X
Karamardian S, Schaible S: Seven kinds of monotone maps. Journal of Optimization Theory and Applications 1990,66(1):37–46. 10.1007/BF00940531
Ruiz-Garzón G, Osuna-Gómez R, Rufián-Lizana A: Generalized invex monotonicity. European Journal of Operational Research 2003,144(3):501–512. 10.1016/S0377-2217(01)00393-9
Yang XM, Yang XQ, Teo KL: Criteria for generalized invex monotonicities. European Journal of Operational Research 2005,164(1):115–119. 10.1016/j.ejor.2003.11.017
Yang XM, Yang XQ, Teo KL: Generalized invexity and generalized invariant monotonicity. Journal of Optimization Theory and Applications 2003,117(3):607–625. 10.1023/A:1023953823177
Fan L, Liu S, Gao S: Generalized monotonicity and convexity of non-differentiable functions. Journal of Mathematical Analysis and Applications 2003,279(1):276–289. 10.1016/S0022-247X(03)00009-X
Jabarootian T, Zafarani J: Generalized invariant monotonicity and invexity of non-differentiable functions. Journal of Global Optimization 2006,36(4):537–564. 10.1007/s10898-006-9006-3
Behera N, Nahak C, Nanda S: Generalized -invexity and generalized -invariant-monotonicity. Nonlinear Analysis: Theory, Methods & Applications 2008,68(8):2495–2506. 10.1016/j.na.2007.02.004
Clarke FH: Optimization and Nonsmooth Analysis, Canadian Mathematical Society Series of Monographs and Advanced Texts. John Wiley & Sons, New York, , NY, USA; 1983:xiii+308.
Weir T, Mond B: Pre-invex functions in multiple objective optimization. Journal of Mathematical Analysis and Applications 1988,136(1):29–38. 10.1016/0022-247X(88)90113-8
Mohan SR, Neogy SK: On invex sets and preinvex functions. Journal of Mathematical Analysis and Applications 1995,189(3):901–908. 10.1006/jmaa.1995.1057
Acknowledgment
This research was partially supported by the National Natural Science Foundation of China (no.10771228 and no.10831009).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, C., Yang, X. Generalized  Invariant Monotonicity and Generalized
Invariant Monotonicity and Generalized  Invexity of Nondifferentiable Functions.
J Inequal Appl 2009, 393940 (2009). https://doi.org/10.1155/2009/393940
Invexity of Nondifferentiable Functions.
J Inequal Appl 2009, 393940 (2009). https://doi.org/10.1155/2009/393940
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/393940
 Invariant Monotonicity and
Invariant Monotonicity and  Invexity
Invexity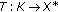 , it is [
, it is [ Invariant Quasimonotonicity and
Invariant Quasimonotonicity and 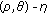 Quasi-Invexity
Quasi-Invexity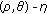 Invariant Pseudomonotonicity and
Invariant Pseudomonotonicity and 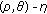 Pseudoinvexity
Pseudoinvexity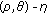 Invariant Pseudomonotonicity and Strongly
Invariant Pseudomonotonicity and Strongly 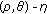 Pseudoinvexity
Pseudoinvexity