On a Two-Step Algorithm for Hierarchical Fixed Point Problems and Variational Inequalities

Abstract

A common method in solving ill-posed problems is to substitute the original problem by a family of well-posed (i.e., with a unique solution) regularized problems. We will use this idea to define and study a two-step algorithm to solve hierarchical fixed point problems under different conditions on involved parameters.

1. Introduction and Preliminar Results

A common method in solving ill-posed problems is to substitute the original problem by a family of well-posed (i.e., with a unique solution) regularized problems. We will use this idea to define and study a two-step algorithm to solve hierarchical fixed point problems under different conditions on involved parameters. We will see that choosing appropriate hypotheses on the parameters, we will obtain convergence to the solution of well-posed problems. Changing these assumptions, we will obtain convergence to one of the solutions of a ill-posed problem. The results are situaded on the lines of research of Byrne [1], Yang and Zhao [2], Moudafi [3], and Yao and Liou [4].

In this paper, we consider variational inequalities of the form

(1.1)

where are nonexpansive mappings such that the fixed points set of () is nonempty and is a nonempty closed convex subset of a Hilbert space . If we denote with the set of solutions of (1.1), it is evident that .

Variational inequalities of (1.1) cover several topics recently investigated in literature as monotone inclusion ([5] and the references therein), convex optimization [6], quadratic minimization over fixed point set (see, e.g., [5, 7–10] and the references therein).

It is well known that the solutions of (1.1) are the fixed points of the nonexpansive mapping .

There are in literature many papers in which iterative methods are defined in order to solve (1.1).

Recently, in [3] Moudafi defined the following explicit iterative algorithm

(1.2)

where and are two sequences in and he proved a weak-convergence's result. In order to obtain a strong-convergence result, Maingé and Moudafi in [11] introduced and studied the following iterative algorithm

(1.3)

where and are two sequences in .

Let be a contraction with coefficient In this paper, under different conditions on involved parameters, we study the algorithm

(1.4)

and give some conditions which assure that the method converges to a solution which solves some variational inequality.

We will confront the two methods (1.3) and (1.4) later.

We recall some general results of the Hilbert spaces theory and of the monotone operators theory.

Lemma 1.1.

For all , there holds the inequality

(1.5)

If is closed convex subset of a real Hilbert space , the metric projection is the mapping defined as follows: for each , is the only point in with the property

(1.6)

Lemma 1.2.

Let be a nonempty closed convex subset of a real Hilbert space and let be the metric projection from onto . Given and , if and only if

(1.7)

Lemma 1.3 (see [7]).

Let be a contraction with coefficient and be a nonexpansive mapping. Then, for all :

(a)the mapping is strongly monotone with coefficient , that is,

(1.8)

(b)the mapping is monotone, that is,

(1.9)

Finally, we conclude this section with a lemma due to Xu on real sequences which has a fundamental role in the sequel.

Lemma 1.4 (see [9]).

Assume is a sequence of nonnegative numbers such that

(1.10)

where is a sequence in and is a sequence in such that,

(1)

(2) or

Then

2. Convergence of the Two-Step Iterative Algorithm

Let us consider the scheme

(2.1)

As we will see the convergence of the scheme depends on the choice of the parameters and . We list some possible hypotheses on them:

(H1)there exists such that ;

(H2);

(H3) as and ;

(H4);

(H5);

(H6);

(H7);

(H8);

(H9)there exists such that .

Proposition 2.1.

Assume that (H1) holds. Then and are bounded.

Proof.

Let . Then,

(2.2)

So, by induction, one can see that

(2.3)

Of course is bounded too.

Proposition 2.2.

Suppose that (H1), (H3) hold. Also, assume that either (H4) and (H5) hold, or (H6) and (H7) hold. Then

(1) is asymptotically regular, that is,

(2.4)

(2)the weak cluster points set .

Proof.

Observing that

(2.5)

then, passing to the norm we have

(2.6)

By definition of one obtain that

(2.7)

so, substituting (2.7) in (2.6) we obtain

(2.8)

By Proposition 2.1, we call so we have

(2.9)

So, if (H4) and (H5) hold, we obtain the asymptotic regularity by Lemma 1.4.

If, instead, (H6) and (H7) hold, from (H1) we can write

(2.10)

so, the asymptotic regularity follows by Lemma 1.4 also.

In order to prove (2), we can observe that

(2.11)

By (H1), and (H3) it follows that , as , so that since is asymptotically regular. By demiclosedness principle we obtain the thesis.

Corollary 2.3.

Suppose that the hypotheses of Proposition 2.2 hold. Then

(i);

(ii);

(iii).

Proof.

To prove we can observe that

(2.12)

The asymptotical regularity of gives the claim.

Moreover, noting that

(2.13)

since as we obtain . In the end follows easily by and .

Theorem 2.4.

Suppose (H2) with and (H3). Moreover Suppose that either (H4) and (H5) hold, or (H6) and (H7) hold. If one denote by the unique element in such that , then

• (1)
  

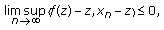  (2.14)

(2) as .

Proof.

First of all, is a contraction, so there exists a unique such that . Moreover, from Lemma 1.2, is characterized by the fact that

(2.15)

Since (H2) implies (H1), thus is bounded. Let be a subsequence of such that

(2.16)

and . Thanks to either ((H4) and (H5)) or ((H6) and (H7)), by Proposition 2.2 it follows that . Then

(2.17)

Now we observe that, by Lemma 1.1

(2.18)

Since then

(2.19)

Thus, by Lemma 1.4, as .

Theorem 2.5.

Suppose that (H2) with , (H3), (H8), (H9) hold. Then , as , where is the unique solution of the variational inequality

(2.20)

Proof.

First of all, we show that (2.20) cannot have more than one solution. Indeed, let and be two solutions. Then, since is solution, for one has

(2.21)

Analogously

(2.22)

Adding (2.21) and (2.22), we obtain

(2.23)

so . Also now the condition (H2) with implies (H1) so the sequence is bounded. Moreover, since (H8) implies (H6) and (H7), then is asymptotically regular. Similarly, by Proposition 2.2, the weak cluster points set of , , is a subset of . Now we have

(2.24)

so that

(2.25)

and denoting by we have

(2.26)

Dividing by in (2.9), one observe that

(2.27)

By Lemma 1.4, we have

(2.28)

so, also is a null sequence as . Fixing , by (2.26) it results

(2.29)

By Lemma 1.3, we obtain that

(2.30)

Now, we observe that

(2.31)

so, since and , as , then every weak cluster point of is also a strong cluster point.

By Proposition 2.2, is bounded, thus there exists a subsequence converging to . For all by (2.26)

(2.32)

Passing to we obtain

(2.33)

which (2.20). Thus, since the (2.20) cannot have more than one solution, it follows that and this, of course, ensures that , as .

Proposition 2.6.

Suppose that (H2) holds with . Suppose that (H3), (H8) and (H9) hold. Moreover let be bounded and be a null sequence. Then every is solution of the variational inequality

(2.34)

that is, .

Proof.

Since (H8) implies (H6) and (H7), by boundedness of , we can obtain its asymptotical regularity as in proof of Proposition 2.2. Moreover, since , as in proof of Proposition 2.2, . With the same notation in proof of Theorem 2.5 we have that

(2.35)

holds for all . So, if and , by (H2), the boundedness of , and of Corollary 2.3 we have

(2.36)

If we change with , , we have

(2.37)

Letting finally

(2.38)

Remark 2.7.

If we choose and (with ), since and it is not difficult to prove that (H8) is satisfied for and (H9) is satisfied if .

Remark 2.8.

It is clear that our algorithm (1.4) is different from (1.3). At the same time, our algorithm (1.4) includes some algorithms in the literature as special cases. For instance, if we take in (1.4), then we get which is well-known as the viscosity method studied by Moudafi [8] and Xu [10].

Remark 2.9.

We do not know the rate of convergence of our method. Nevertheless, the rates of convergence of our method (1.4) that generates the sequence and the Mainge-Moudafi method (1.3), seem not comparable. To see this, we consider three examples. In such examples we take , , , , .

In all three examples all the assumptions (that are the same of the Mainge-Moudafi method) are satisfied and the point at which both the sequences and converge is .

Example 2.10.

Take and . Then

(2.39)

while

(2.40)

Now , while, for , it results . For instance, we report here some value

(2.41)

However from the 64th iteration onward, becomes quickly very exiguous with respect to . For instance, while .

Example 2.11.

Take . Then

(2.42)

while

(2.43)

that is the sequences and are interchanged with respect to the previous example. So this time for and for .

Example 2.12.

Take , . Then

(2.44)

so this time .

Reassuming, we cannot affirm that our method is more convenient or better than the Mainge-Moudafi method, but only that seems to us that it is the first time that it is introduced a two-step iterative approach to the VIP (1.1). In some case, our method approximates the solution more rapidly than Mainge-Moudafi method, in some other case it happens the contrary and in some other cases, both methods give the same sequence.