- Research Article
- Open access
- Published:
A Kind of Estimate of Difference Norms in Anisotropic Weighted Sobolev-Lorentz Spaces
Journal of Inequalities and Applications volume 2009, Article number: 161405 (2009)
Abstract
We investigate the functions spaces on  for which the generalized partial derivatives
for which the generalized partial derivatives  exist and belong to different Lorentz spaces
exist and belong to different Lorentz spaces  , where
, where  and
and  is nonincreasing and satisfies some special conditions. For the functions in these weighted Sobolev-Lorentz spaces, the estimates of the Besov type norms are found. The methods used in the paper are based on some estimates of nonincreasing rearrangements and the application of
is nonincreasing and satisfies some special conditions. For the functions in these weighted Sobolev-Lorentz spaces, the estimates of the Besov type norms are found. The methods used in the paper are based on some estimates of nonincreasing rearrangements and the application of  ,
,  weights.
weights.
1. Introduction
In this paper we study functions  on
on  which possess the generalized partial derivatives
which possess the generalized partial derivatives

Our main goal is to obtain some norm estimates for the differences

( being the unit coordinate vector).
being the unit coordinate vector).
The classic Sobolev embedding theorem asserts that for any function  in Sobolev space
in Sobolev space 

Sobolev proved this inequality in 1938 for  . His method, based on integral representations, did not work in the case
. His method, based on integral representations, did not work in the case  . Only at the end of fifties Gagliardo and Nirenberg gave simple proofs of inequality (1.3) for all
. Only at the end of fifties Gagliardo and Nirenberg gave simple proofs of inequality (1.3) for all  Inequality (1.3) has been generalized in various directions (see [1–6] for details). It was proved that the left hand side in (1.3) can be replaced by the stronger Lorentz norm, that is, there holds the inequality
Inequality (1.3) has been generalized in various directions (see [1–6] for details). It was proved that the left hand side in (1.3) can be replaced by the stronger Lorentz norm, that is, there holds the inequality

For  the result follows by interpolation (see [7, 8]). In the case
the result follows by interpolation (see [7, 8]). In the case  some geometric inequalities were applied to prove (1.4) (see [9–13]).
some geometric inequalities were applied to prove (1.4) (see [9–13]).
The sharp estimates of the norms of differences for the functions in Sobolev spaces have firstly been proved by Besov et al. [1, Volume 2, page 72]. For the space  Il'in's result reads as follows: If
Il'in's result reads as follows: If  and
and  then
then

Actually, this means that there holds the continuous embedding to the Besov space

It is easy to see that inequality (1.5) fails to hold for  , but, it was proved in [14] that (1.5) is true for
, but, it was proved in [14] that (1.5) is true for  and
and  .
.
The generalization of the inequality (1.5) to the spaces  was given in [12]. That is
was given in [12]. That is

where  and
and  the inequality is valid if
the inequality is valid if  or
or  Using (1.7), we get the following continuous embedding:
Using (1.7), we get the following continuous embedding:

For  this embedding was proved by Besov et al. [1, Volume 2, page 72]. The main result in [12] is the proof of (1.7) for
this embedding was proved by Besov et al. [1, Volume 2, page 72]. The main result in [12] is the proof of (1.7) for  .
.
In [15], there was the sharp estimates of the type (1.7) when the derivatives  belong to different Lorentz spaces
belong to different Lorentz spaces  Before stating the theorem, we give some notations. Let
Before stating the theorem, we give some notations. Let  be the class of all measurable and almost everywhere finite functions
be the class of all measurable and almost everywhere finite functions  on
on  such that for each
such that for each  ,
,

Let  and
and  for
for  Denote
Denote

Now we state the main theorem in [15].
Theorem 1.1.
Let  , and
, and  if
if  . Let
. Let  , and
, and  be the numbers defined by (1.10). For every
be the numbers defined by (1.10). For every  satisfying the condition
satisfying the condition

take arbitrary  such that
such that

and denote

then for any function  which has the weak derivatives
which has the weak derivatives  there holds the inequality
there holds the inequality

where  is a constant that does not depend on
is a constant that does not depend on  .
.
In many cases, the Lorentz space should be substituted by more general space, the weighted Lorentz space. In this paper, we will generalize the above result when the weighted Lorentz spaces  take place of
take place of  , where
, where  is a weight on
is a weight on  which satisfies some special conditions.
which satisfies some special conditions.
2. Auxiliary Proposition
Let  be the class of all measurable and almost everywhere finite functions on
be the class of all measurable and almost everywhere finite functions on  . For
. For  , a nonincreasing rearrangement of
, a nonincreasing rearrangement of  is a nonincreasing function
is a nonincreasing function  on
on  that is, equimeasurable with
that is, equimeasurable with  . The rearrangement
. The rearrangement  can be defined by the equality
can be defined by the equality

where

If  then the following relation holds [16, Chapter 2]:
then the following relation holds [16, Chapter 2]:

Set

Assume that  A function
A function  belongs to the Lorentz space
belongs to the Lorentz space  if
if

For  , the space
, the space  is defined as the class of all
is defined as the class of all  such that
such that

We also let  . Let
. Let  be a weight in
be a weight in  (nonnegative locally integrable functions in
(nonnegative locally integrable functions in  ).
).
If  , we replace
, we replace  with
with  . For
. For  , or
, or  and
and  , the weighted Lorentz space
, the weighted Lorentz space  is defined in [9, Chapter 2] by
is defined in [9, Chapter 2] by

If  , denote
, denote  It is well known that
It is well known that

and if  then
then

where

In following part of this paper, we will always denote  .
.
The weighted Lorentz spaces have close connection with weights of  for
for  (see [9, Chapter 1]). Let
(see [9, Chapter 1]). Let  be the Hardy operator as follows:
be the Hardy operator as follows:

The space  is the cone of all nonnegative nonincreasing functions in
is the cone of all nonnegative nonincreasing functions in  . We denote
. We denote  if
if

is bounded and denote  if
if

is bounded.
Lemma 2.1 (Generalized Hardy's inequalities).
Let  be nonnegative, measurable on
be nonnegative, measurable on  and suppose
and suppose  and
and  is a weight in
is a weight in  ,
,  then one has
then one has

(with the obvious modification if  ).
).
Proof.
It is easy to obtain this result applying Hardy's inequality [16].
Lemma 2.2.
Let  be a nonnegative nonincreasing function on
be a nonnegative nonincreasing function on  ,
,  be a nonincreasing weight on
be a nonincreasing weight on  and there exists
and there exists  , such that
, such that

Then for  there exists a continuously differentiable
there exists a continuously differentiable  on
on  such that
such that
(i)
(ii) decreases and
decreases and  increases on
increases on  ,
,
(iii)
where  is a constant depends only on
is a constant depends only on  , and
, and  .
.
Proof.
Without loss of generality, we may suppose that  . Set
. Set

Then  decreases and
decreases and

Using the conditions which  satisfy, it gives
satisfy, it gives

Furthermore, noticing  is nonincreasing and applying Lemma 2.1, we get that
is nonincreasing and applying Lemma 2.1, we get that

now set

Then  increases on
increases on  , and
, and

Furthermore,

where  that is,
that is,  . Since
. Since  is decreasing function on
is decreasing function on  , thus
, thus  is decreasing and
is decreasing and  is also decreasing on
is also decreasing on  .
.
Finally, using Lemma 2.1 and (2.19), we get (iii). The Lemma 2.2 is proved.
Let  and
and  for
for  Denote
Denote

Then  and
and

To prove our main results we use the estimates of the rearrangement of a given function in term of its derivatives 
We will use the notations (2.23).
Lemma 2.3.
Let  for
for  and
and  is continuous weight on
is continuous weight on  . Set
. Set

Let

and suppose that  are positive continuously differentiable functions with
are positive continuously differentiable functions with  on
on  such that
such that  decreases and
decreases and  increases on
increases on  . Set for
. Set for 


Then
(i)there holds the inequality

(ii)there exist continuously differentiable functions  on
on  such that
such that

(iii)for any  such that
such that

the function  decreases on
decreases on  .
.
Proof.
The proof is similar to [15, Lemma  ]. All the argument holds true when we substitute the weight
]. All the argument holds true when we substitute the weight  in this lemma for
in this lemma for  .
.
The Lebesgue measure of a measurable set  will be denoted by
will be denoted by  .
.
For any  set
set  denote by
denote by  the orthogonal projection of
the orthogonal projection of  onto the coordinate hyperplane
onto the coordinate hyperplane  . By the Loomis-Whitney inequality [17, Chapter 4]
. By the Loomis-Whitney inequality [17, Chapter 4]

Let  , and let
, and let  be a set of type
be a set of type  and measure
and measure  such that
such that  for all
for all  . Denote by
. Denote by  the
the  -dimensional measure of the projection
-dimensional measure of the projection  By (2.32), we have that
By (2.32), we have that

Lemma 2.4.
Let  be nonincreasing, and
be nonincreasing, and  when
when  where
where  . Function
. Function  has weak derivatives
has weak derivatives  Then for all
Then for all  and
and  one has
one has

where  and
and  is a constant depending on
is a constant depending on  and
and  .
.
Proof.
Let  then
then

Due to the conditions of  and (2.33), we can get
and (2.33), we can get


So we immediately get (2.34).
Lemma 2.5.
If  and
and  , then
, then 
Proof.
Let  Since
Since  so by [9, Chapter 1] we get
so by [9, Chapter 1] we get

Then

where

So 
Lemma 2.6.
Let  for
for  Assume that weight
Assume that weight  on
on  satisfies the following conditions:
satisfies the following conditions:
(i)it is nonincreasing, continuous, and  ,
,
(ii)exists  such that
such that

Set

Assume that a locally integrable function  has weak derivatives
has weak derivatives  Then for any
Then for any 

where  the constants
the constants  depends only on
depends only on  , and
, and

Proof.
For every fixed  we take
we take

Thanks to Lemma 2.5, and  (for
(for  is nonincreasing), we know
is nonincreasing), we know

Thus

Next we apply Lemma 2.2 with  defined as in Lemma 2.3. In this way we obtain the functions which we denote by
defined as in Lemma 2.3. In this way we obtain the functions which we denote by  . Further, with these functions
. Further, with these functions  we define the function
we define the function  by (2.28). By Lemma 2.3, we have the inequality (2.44). Using Lemma 2.4 with
by (2.28). By Lemma 2.3, we have the inequality (2.44). Using Lemma 2.4 with  we obtain
we obtain

where  . Taking into account (2.28), we get (2.43).
. Taking into account (2.28), we get (2.43).
Corollary 2.7.
Let  for
for  and
and  be the numbers defined by (2.42). Assume weight
be the numbers defined by (2.42). Assume weight  on
on  satisfies the following conditions:
satisfies the following conditions:
(i)it is nonincreasing, continuous, and  ,
,
(ii)there exist two constants  with
with  such that
such that

and there holds

Assume that a locally integrable function  has weak derivatives
has weak derivatives  and
and  for some
for some  with
with  such that
such that

Let  and
and

Then  and
and

Proof.
Let  , with
, with  and
and  . Applying Hölder's inequality and noticing
. Applying Hölder's inequality and noticing  and
and  is nonincreasing, we obtain
is nonincreasing, we obtain

So

Let  . Using (2.43) with
. Using (2.43) with  , which satisfies
, which satisfies  (
( are two constants in (2.49) for
are two constants in (2.49) for  ), combining (2.49), (2.52), and Hölder's inequality, we get
), combining (2.49), (2.52), and Hölder's inequality, we get

By (2.55),  Furthermore, from (2.49), we can get
Furthermore, from (2.49), we can get

Inequality (2.53) now follows from (2.44) and (2.55).
Remark 2.8.
If  in Corollary 2.7, then it is easy to get
in Corollary 2.7, then it is easy to get  .
.
Remark 2.9.
Let  for
for  . Let
. Let  , and
, and  be the numbers defined by (2.42). Assume that
be the numbers defined by (2.42). Assume that  ,
,  and
and  satisfies the conditions of Corollary 2.7 with
satisfies the conditions of Corollary 2.7 with  . Then for any function
. Then for any function  with compact support we have
with compact support we have

This statement can be easily got from Lemma 2.6. Inequality (2.58) gives a generalization of Remark  of [15] when
of [15] when  because
because  satisfies the preceding conditions.
satisfies the preceding conditions.
Remark 2.10.
Beyond constant weights, there are many weights satisfying conditions of Corollary 2.7. For example,
(i) where
where 
-
(ii)
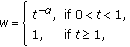 (2.59)
(2.59)
where 
For weight  in (i) or (ii), it is easy to see the weighted Lorentz space
in (i) or (ii), it is easy to see the weighted Lorentz space  for
for  does not coincide with any Lorentz space
does not coincide with any Lorentz space  .
.
3. The Main Theorem
Theorem 3.1.
Let  for
for  Let
Let  , and
, and  be the numbers defined by (2.42). Suppose weight
be the numbers defined by (2.42). Suppose weight  on
on  satisfies the following conditions:
satisfies the following conditions:
(i)it is nonincreasing, continuous, and 
(ii)there exist two constants  with
with  such that
such that

and there holds

For every  satisfying the condition
satisfying the condition

take arbitrary  such that
such that  and
and

and denote

Then for any function  with the weak derivatives
with the weak derivatives  there holds the inequality
there holds the inequality

where  is a constant that does not depend on
is a constant that does not depend on  .
.
Proof.
First we can get  by our conditions. denote
by our conditions. denote

Further, assume that  and set for
and set for 

For almost all  we have [1, Volume 1, page 101]
we have [1, Volume 1, page 101]

Thus,

Indeed, for any subset  with
with 

(3.10) then follows.
For  is nonincreasing (
is nonincreasing ( ), we get
), we get  by Lemma 2.5. Thus from (3.10)
by Lemma 2.5. Thus from (3.10)

It follows  Furthermore
Furthermore

Then due to Hardy lemma [16, page 56]

It follows  Analogically we get
Analogically we get  Thus by Corollary 2.7 we have
Thus by Corollary 2.7 we have  .
.
Denote for 

Set  (
( are two constants in (3.1) for
are two constants in (3.1) for  ), and
), and

where  is the constant in Lemma 2.5. Then by (3.1)
is the constant in Lemma 2.5. Then by (3.1)

Therefore ,

Let

Now for every  by applying Lemma 2.2 with
by applying Lemma 2.2 with  We obtain
We obtain  on
on  such that
such that



For  , it follows that
, it follows that

Thus

We will estimate  for fixed
for fixed  and
and  By Lemma 2.4, (3.21), we have that for each
By Lemma 2.4, (3.21), we have that for each 

where  Applying Lemma 2.3, we obtain that there exist a nonnegative function
Applying Lemma 2.3, we obtain that there exist a nonnegative function  and positive continuously differentiable functions
and positive continuously differentiable functions  on
on  satisfying the following conditions:
satisfying the following conditions:





Denote

We will prove that for any  and any
and any 

where

By (3.24)

For  the inequality (3.32) follows directly from (3.26) and (3.33). If
the inequality (3.32) follows directly from (3.26) and (3.33). If  then (3.32) is the immediate consequence of (3.10), (3.21), and (3.33).
then (3.32) is the immediate consequence of (3.10), (3.21), and (3.33).
Now, taking into account (3.26) and (3.32), we obtain that for  and any
and any 

where

and  is defined by (3.33).
is defined by (3.33).
Further, we have (see (3.18)

By (3.30), the function  increases on
increases on  . It follows easily that
. It follows easily that  exists on
exists on  and satisfies
and satisfies  and
and

Furthermore, we have

Using Minkowsi's inequality, we obtain

Further, using Hölder's inequality and (3.38), we get when  (the case
(the case  is obvious)
is obvious)

Thus, by Fubini's theorem and (3.33)

The same argument gives that

By (3.33) the last integral is the same as one on the right side of (3.42). So, we have that

Now we apply Hölder's inequality with the exponents  and
and  Observe that
Observe that

Therefore, we get, applying (3.27) and (3.34)

Since

we get the inequality (3.6). The theorem is proved.
Let  be a rearrangement invariant space (r.i. space),
be a rearrangement invariant space (r.i. space),  be an r.i. space over
be an r.i. space over  and
and  . Set
. Set  integral part of
integral part of  ). The Besov space
). The Besov space  is defined as follows (see [18, 19]):
is defined as follows (see [18, 19]):

where

and  denotes the fundamental function of
denotes the fundamental function of  with
with  being any measurable subset of
being any measurable subset of  with
with  .
.
Then we have the following.
Corollary 3.2.
Let  for
for  and
and

Let the weight  be the same as that in Theorem 3.1. Take arbitrary
be the same as that in Theorem 3.1. Take arbitrary  such that
such that

and denote

Then for any function  which has the weak derivatives
which has the weak derivatives  there hold
there hold

where  is a constant that does not depend on
is a constant that does not depend on  .
.
Proof.
We can easily obtain the similar result to Lemma  in [20] by substituting
in [20] by substituting  for
for  there. Now the corollary is obvious using the Hardy's inequality and Theorem 3.1.
there. Now the corollary is obvious using the Hardy's inequality and Theorem 3.1.
Remark 3.3.
If there exists  with
with  , whether Theorem 3.1 remains true is still a question now.
, whether Theorem 3.1 remains true is still a question now.
References
Besov OV, Il'in VP, Nikol'skiĭ SM: Integral Representations of Functions and Imbedding Theorems. Vol. I. V. H. Winston & Sons, Washington, DC, USA; 1978:viii+345.
Kolyada VI: Rearrangements of functions and embedding of anisotropic spaces of Sobolev type. East Journal on Approximations 1998,4(2):111–199.
Kudryavtsev LD, Nikol'skiĭ SM: Spaces of differentiable functions of several variables and imbedding theorems. In Analysis, Encyclopaedia Math. Sci.. Volume 26. Springer, Berlin, Germany; 1991:1–140.
Nikol'skií SM: Approximation of Functions of Several Variables and Imbedding Theorems. Springer, New York, NY, USA; 1975:viii+418.
Triebel H: Theory of Function Spaces, Monographs in Mathematics. Volume 78. Birkhäuser, Basel, Switzerland; 1983:284.
Triebel H: Theory of Function Spaces. II, Monographs in Mathematics. Volume 84. Birkhäuser, Basel, Switzerland; 1992:viii+370.
Peetre J: Espaces d'interpolation et théorème de Soboleff. Université de Grenoble. Annales de l'Institut Fourier 1966,16(1):279–317. 10.5802/aif.232
Strichartz RS: Multipliers on fractional Sobolev spaces. Journal of Mathematics and Mechanics 1967, 16: 1031–1060.
Carro MJ, Raposo JA, Soria J: Recent developments in the theory of Lorentz spaces and weighted inequalities. Memoirs of the American Mathematical Society 2007.,187(877):
Faris WG: Weak Lebesgue spaces and quantum mechanical binding. Duke Mathematical Journal 1976,43(2):365–373. 10.1215/S0012-7094-76-04332-5
Kolyada VI: Rearrangements of functions, and embedding theorems. Uspekhi Matematicheskikh Nauk 1989,44(5):61–95. [English translation: Russian Math. Surveys, vol. 44, no. 5, pp. 73–118, 1989] [English translation: Russian Math. Surveys, vol. 44, no. 5, pp. 73–118, 1989]
Kolyada VI: On the embedding of Sobolev spaces. Matematicheskie Zametki 1993,54(3):48–71. [English translation: Math. Notes, vol. 54, no. 3, pp. 908–922, 1993] [English translation: Math. Notes, vol. 54, no. 3, pp. 908–922, 1993]
Poornima S: An embedding theorem for the Sobolev space
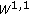 . Bulletin des Sciences Mathématiques 1983,107(3):253–259.
. Bulletin des Sciences Mathématiques 1983,107(3):253–259.Kolyada VI: On the relations between moduli of continuity in various metrics. Trudy Matematicheskogo Instituta imeni V. A. Steklova 1988, 181: 117–136. [English translation: Proc. Steklov Inst. Math., vol. 4, pp. 127–148, 1989] [English translation: Proc. Steklov Inst. Math., vol. 4, pp. 127–148, 1989]
Kolyada VI, Pérez FJ: Estimates of difference norms for functions in anisotropic Sobolev spaces. Mathematische Nachrichten 2004, 267: 46–64. 10.1002/mana.200310152
Bennett C, Sharpley R: Interpolation of Operators, Pure and Applied Mathematics. Volume 129. Academic Press, Boston, Mass, USA; 1988:xiv+469.
Hadwiger H: Vorlesungen über Inhalt, Oberfläche und Isoperimetrie. Springer, Berlin, Germany; 1957:xiii+312.
Martín J, Milman M: Symmetrization inequalities and Sobolev embeddings. Proceedings of the American Mathematical Society 2006,134(8):2335–2347. 10.1090/S0002-9939-06-08277-3
Martín J, Milman M: Higher-order symmetrization inequalities and applications. Journal of Mathematical Analysis and Applications 2007,330(1):91–113. 10.1016/j.jmaa.2006.07.033
Kolyada VI: Inequalities of Gagliardo-Nirenberg type and estimates for the moduli of continuity. Uspekhi Matematicheskikh Nauk 2005,60(6):139–156. [English translation: Russian Math. Surveys, vol. 60, no. 6, pp. 1147–1164] [English translation: Russian Math. Surveys, vol. 60, no. 6, pp. 1147–1164]
Acknowledgments
This work is supported by NSFC (no. 10571156, 10871173), Natural Science Foundation of Zhejiang Province (no. Y606117), Foundation of Zhejiang Province Education Department (no. Y200803879) and 2008 Excellent Youth Foundation of College of Zhejiang Province (no. 01132047).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, J., Li, H. A Kind of Estimate of Difference Norms in Anisotropic Weighted Sobolev-Lorentz Spaces. J Inequal Appl 2009, 161405 (2009). https://doi.org/10.1155/2009/161405
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/161405
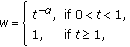
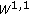 . Bulletin des Sciences Mathématiques 1983,107(3):253–259.
. Bulletin des Sciences Mathématiques 1983,107(3):253–259.