- Research Article
- Open access
- Published:
Sufficient Conditions for Univalence of an Integral Operator Defined by Al-Oboudi Differential Operator
Journal of Inequalities and Applications volume 2008, Article number: 957042 (2008)
Abstract
We investigate the univalence of an integral operator defined by Al-Oboudi differential operator.
1. Introduction
Let  denote the class of all functions of the form
denote the class of all functions of the form

which are analytic in the open unit disk  , and
, and  .
.
For  , Al-Oboudi [1] introduced the following operator:
, Al-Oboudi [1] introduced the following operator:



If  is given by (1.1), then from (1.3) and (1.4) we see that
is given by (1.1), then from (1.3) and (1.4) we see that

with  .
.
When  , we get Sălăgean's differential operator [2].
, we get Sălăgean's differential operator [2].
By using the Al-Oboudi differential operator, we introduce the following integral operator.
Definition 1.1.
Let  and
and  ,
,  . We define the integral operator
. We define the integral operator  ,
,

where  and
and  is the Al-Oboudi differential operator.
is the Al-Oboudi differential operator.
Remark 1.2.
-
(i)
For
 ,
, 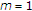 ,
,  ,
, 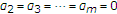 , and
, and 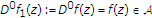 , we have Alexander integral operator
, we have Alexander integral operator  (1.7)
(1.7)
which was introduced in [3].
-
(ii)
For
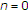 ,
, 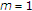 ,
,  ,
, 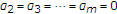 , and
, and 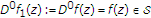 , we have the integral operator
, we have the integral operator 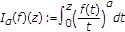 (1.8)
(1.8)
that was studied in [4].
-
(iii)
For
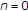 ,
, 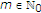 ,
, 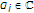 ,
,  ,
, 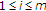 , we have the integral operator
, we have the integral operator  (1.9)
(1.9)
which was studied in [5].
-
(iv)
For
 ,
, 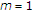 ,
,  ,
, 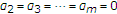 and
and 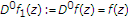 , we have the integral operator
, we have the integral operator 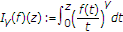 (1.10)
(1.10)
2. Main Results
The following lemmas will be required in our investigation.
Lemma 2.1 (see [8]).
If the function  is regular in the unit disk
is regular in the unit disk  ,
,  , and
, and

for all  , then the function
, then the function  is univalent in
is univalent in  .
.
Lemma 2.2 (Schwarz Lemma 2.2) (see [9, page 166]).
Let the analytic function  be regular in
be regular in  and let
and let  . If, in
. If, in  ,
,  , then
, then

and  .
.
The equality holds if and only if  and
and  .
.
Theorem 2.3.
Let  ,
,  , and
, and  ,
,  . If
. If

then  defined in Definition 1.1 is univalent in
defined in Definition 1.1 is univalent in  .
.
Proof. .
Since  ,
,  , by (1.5), we have
, by (1.5), we have

for all  .
.
On the other hand, we obtain

for  . This equality implies that
. This equality implies that

or equivalently

By differentiating the above equality, we get

After some calculus, we obtain

By hypothesis, since  , and since
, and since  we have
we have

So, we obtain

Thus  .
.
Remark 2.4.
For  ,
,  ,
,  , we have [5, Theorem 1].
, we have [5, Theorem 1].
Corollary 2.5.
Let  ,
,  and
and  ,
,  . If
. If

and  , then
, then  .
.
Theorem 2.6.
Let  ,
,  and
and  ,
,  . If
. If
(i) ,
,
(ii) , and
, and
(iii) ,
,
then  defined in Definition 1.1 is univalent in
defined in Definition 1.1 is univalent in  .
.
Proof. .
By (2.9), we get

This inequality implies that

By Schwarz lemma (Lemma 2.2), we have

or

for all  .
.
So, by Lemma 2.1,  .
.
Remark 2.7.
For  ,
,  ,
,  ,
,  ,
,  , we have [7, Theorem 1].
, we have [7, Theorem 1].
Corollary 2.8.
Let  ,
,  and
and  ,
,  . If
. If
(i) ,
,
(ii) , and
, and
(iii) ,
,
then  .
.
In [10], similar results are given by using the Ruscheweyh differential operator.
References
Al-Oboudi FM: On univalent functions defined by a generalized Sălăgean operator. International Journal of Mathematics and Mathematical Sciences 2004,2004(27):1429–1436. 10.1155/S0161171204108090
Sălăgean GŞ: Subclasses of univalent functions. In Complex Analysis—Fifth Romanian-Finnish Seminar, Part 1 (Bucharest, 1981), Lecture Notes in Mathematics. Volume 1013. Springer, Berlin, Germany; 1983:362–372. 10.1007/BFb0066543
Alexander JW: Functions which map the interior of the unit circle upon simple regions. Annals of Mathematics 1915,17(1):12–22. 10.2307/2007212
Miller SS, Mocanu PT, Reade MO: Starlike integral operators. Pacific Journal of Mathematics 1978,79(1):157–168.
Breaz D, Breaz N: Two integral operators. Studia Universitatis Babeş-Bolyai, Mathematica 2002,47(3):13–19.
Pescar V: On some integral operations which preserve the univalence. The Punjab University. Journal of Mathematics 1997, 30: 1–10.
Pescar V, Owa S: Sufficient conditions for univalence of certain integral operators. Indian Journal of Mathematics 2000,42(3):347–351.
Becker J: Löwnersche Differentialgleichung und quasikonform fortsetzbare schlichte Funktionen. Journal für die Reine und Angewandte Mathematik 1972, 255: 23–43.
Nehari Z: Conformal Mapping. Dover, New York, NY, USA; 1975:vii+396.
Oros GI, Oros G, Breaz D: Sufficient conditions for univalence of an integral operator. Journal of Inequalities and Applications 2008, 2008:-7.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bulut, S. Sufficient Conditions for Univalence of an Integral Operator Defined by Al-Oboudi Differential Operator. J Inequal Appl 2008, 957042 (2008). https://doi.org/10.1155/2008/957042
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/957042
 ,
, 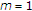 ,
,  ,
, 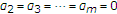 , and
, and 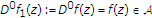 , we have Alexander integral operator
, we have Alexander integral operator 
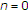 ,
, 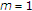 ,
,  ,
, 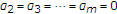 , and
, and 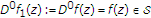 , we have the integral operator
, we have the integral operator 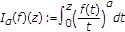
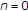 ,
, 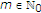 ,
, 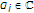 ,
,  ,
, 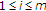 , we have the integral operator
, we have the integral operator 
 ,
, 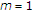 ,
,  ,
, 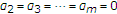 and
and 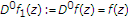 , we have the integral operator
, we have the integral operator