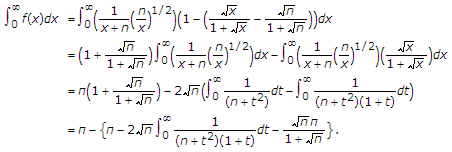- Research Article
- Open access
- Published:
On a New Weighted Hilbert Inequality
Journal of Inequalities and Applications volume 2008, Article number: 637397 (2008)
Abstract
It is shown that a weighted Hilbert inequality for double series can be established by introducing a proper weight function. Thus, a quite sharp result of the classical Hilbert inequality for double series is obtained. And a similar result for the Hilbert integral inequality is also proved. Some applications are considered.
1. Introduction
Let  and
and  be two sequences of real numbers. It is all known that the inequality
be two sequences of real numbers. It is all known that the inequality

is called Hilbert theorem for double series [1], where  , and the constant factor
, and the constant factor  in (1.1) is the best possible value. And the equality in (1.1) holds if and only if
in (1.1) is the best possible value. And the equality in (1.1) holds if and only if  or
or  is a zero-sequence. The corresponding integral form of (1.1) is that
is a zero-sequence. The corresponding integral form of (1.1) is that

where  , and the constant factor
, and the constant factor  in (1.2) is the best possible value. Recently, various improvements and extensions of (1.1) and (1.2) appear in a great deal of papers (see [2–6], etc.). The aim of the present paper is to build some new inequalities by using the weight function method and the technique of analysis, and then to study some applications of them.
in (1.2) is the best possible value. Recently, various improvements and extensions of (1.1) and (1.2) appear in a great deal of papers (see [2–6], etc.). The aim of the present paper is to build some new inequalities by using the weight function method and the technique of analysis, and then to study some applications of them.
First we give some lemmas.
Lemma 1.1.
Let  be a positive integer. Then
be a positive integer. Then

Proof.
Let  be real numbers. Then
be real numbers. Then

where  is an arbitrary constant. This result is given in the paper (see [7]). Based on this indefinite integral it is easy to deduce that the equality (1.3) holds.
is an arbitrary constant. This result is given in the paper (see [7]). Based on this indefinite integral it is easy to deduce that the equality (1.3) holds.
Lemma 1.2.
If  and
and  , where
, where  , then
, then
(1) and
and  are monotonously decreasing in interval
are monotonously decreasing in interval  ;
;
-
(2)
 (1.5)
(1.5)
where the weight function  is defined by
is defined by

.
Proof.
-
(1)
At first, notice that
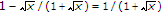 , hence we can write
, hence we can write 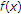 in the form of:
in the form of: 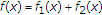 , where
, where 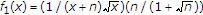 and
and 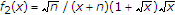 . It is obvious that the functions
. It is obvious that the functions 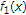 and
and 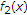 are monotonously decreasing in
are monotonously decreasing in 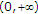 . So,
. So, 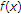 is also monotonously decreasing in
is also monotonously decreasing in 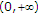 . In the next place, notice that
. In the next place, notice that  , therefore we can write
, therefore we can write 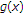 in the form of:
in the form of: 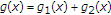 , where
, where 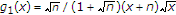 and
and 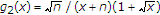 . It is clear that the functions
. It is clear that the functions 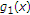 and
and 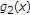 are monotonously decreasing in
are monotonously decreasing in  . So,
. So, 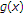 is also monotonously decreasing in
is also monotonously decreasing in  .
. -
(2)
Below, we need only to compute the first integral,
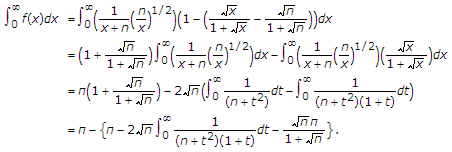 (1.7)
(1.7)
By Lemma 1.1, we obtain the first integral of (1.5) at once after some simple computations and simplifications.
Similarly, the second integral of (1.5) can be gotten.
Lemma 1.3.
Let  be a sequence of real numbers, and let
be a sequence of real numbers, and let  be a real function and
be a real function and  . If
. If  , then
, then

Proof.
It is obvious that

We need only to show that

Let  Then
Then

Lemma 1.4.
Let  be a real number, and let
be a real number, and let  and
and  be two real functions, and
be two real functions, and  and
and  , where
, where  . Then
. Then

.
Its proof is similar to that of Lemma 1.3. Hence, it is omitted.
2. Main Results
Theorem 2.1.
Let  and
and  be two sequences of real numbers. If
be two sequences of real numbers. If  and
and  , then
, then

where the weight function  is defined by (1.6).
is defined by (1.6).
Proof.
Let  be a real function and it satisfies condition
be a real function and it satisfies condition  First, we suppose that
First, we suppose that  . By Lemma 1.3 and then applying Cauchy's inequality we have
. By Lemma 1.3 and then applying Cauchy's inequality we have

where

It is easy to deduce that

Let  . It is obvious that
. It is obvious that  for
for  and
and  . Consider the function
. Consider the function  By Lemma 1.2, the function
By Lemma 1.2, the function  is monotonously decreasing in
is monotonously decreasing in  . Hereby, we have
. Hereby, we have

Using (1.5), we can obtain immediately

Similarly, we have

It follows from (2.2), (2.6), and (2.7) that

where the weight function  is defined by (1.6).
is defined by (1.6).
Next, consider the case for  We can apply Schwarz's inequality to estimate the left-hand side of (2.1) as follows:
We can apply Schwarz's inequality to estimate the left-hand side of (2.1) as follows:

And then by using the inequality (2.8), the inequality (2.1) follows from (2.9) at once. It is obvious that the inequality (2.1) is a refinement of (1.1). Below, we give an extension of (1.2).
Theorem 2.2.
Let  be a real number,
be a real number,  and
and  , and let
, and let  and
and  be two real functions, and
be two real functions, and  and
and  . Then
. Then

where the weight function  is defined by
is defined by

Specially, when  , it is a refinement of (1.2).
, it is a refinement of (1.2).
Proof.
Let  be a real function, and
be a real function, and 
 .
.
Firstly, we suppose that  . Using Lemma 1.4 and then applying Cauchy's inequality we have
. Using Lemma 1.4 and then applying Cauchy's inequality we have

where

In the first place, we consider  :
:

where

We need only to compute the weight function  .
.
Let us select still  . Then
. Then  . Using (1.4), we have
. Using (1.4), we have

Notice that  . Hence, the function defined by (2.11) is just. So, we attain
. Hence, the function defined by (2.11) is just. So, we attain

Similarly, we have

We obtain from (2.12), (2.17), and (2.18) that

where the weight function  is defined by (2.11).
is defined by (2.11).
Secondly, consider the case for  . We can apply Schwarz's inequality to estimate the left-hand side of (2.10) as follows:
. We can apply Schwarz's inequality to estimate the left-hand side of (2.10) as follows:

It follows from (2.19) and (2.20) that the inequality (2.10) is valid.
3. Applications
As applications, we will give some new refinements of Hardy-Littlewood's theorem and Widder's theorem below.
Let  and
and  for all
for all  . Define a sequence
. Define a sequence  by
by

Hardy-Littlewood [1] proved that

where  is the best constant that the inequality (3.2) keeps valid.
is the best constant that the inequality (3.2) keeps valid.
Theorem 3.1.
With the assumptions as the above-mentioned, define a sequence  by
by  . Then
. Then

where  is defined by (1.6).
is defined by (1.6).
Proof.
By our assumptions, we may write  in the form of:
in the form of: 
Apply Schwarz's inequality to estimate the left-hand side of (3.3) as follows:

It is known from (2.8) and (3.4) that the inequality (3.3) is valid. Theorem is therefore proved.
Let  and
and  . Then
. Then

This is the famous Widder theorem (see [1]).
Theorem 3.2.
With the assumptions as the above-mentioned, then

where  is defined by (2.11).
is defined by (2.11).
Proof.
First, we have the following relation:

Let  . Then we have
. Then we have

where  . By using (2.19), the inequality (3.6) follows from (3.8) at once.
. By using (2.19), the inequality (3.6) follows from (3.8) at once.
References
Hardy GH, Littlewood JE, Pólya G: Inequalities. Cambridge University Press, Cambridge, UK; 1952:xii+324.
Gao M, Hsu LC: A survey of various refinements and generalizations of Hilbert's inequalities. Journal of Mathematical Research and Exposition 2005,25(2):227–243.
Gao M, Yang B: On the extended Hilbert's inequality. Proceedings of the American Mathematical Society 1998,126(3):751–759. 10.1090/S0002-9939-98-04444-X
Yang B, Debnath L: On a new generalization of Hardy-Hilbert's inequality and its applications. Journal of Mathematical Analysis and Applications 1999,233(2):484–497. 10.1006/jmaa.1999.6295
Jichang K, Debnath L: On new generalizations of Hilbert's inequality and their applications. Journal of Mathematical Analysis and Applications 2000,245(1):248–265. 10.1006/jmaa.2000.6766
He L, Gao M, Wei S: A note on Hilbert's inequality. Mathematical Inequalities and Applications 2003,6(2):283–288.
Jin Y: Applied Integral Tables. Chinese Science and Technology University Press, Hefei, China; 2006.
Acknowledgment
This work is a project supported by Scientific Research Fund of Hunan Provincial Education Department (07C520 and 06C657).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Leping, H., Xuemei, G. & Mingzhe, G. On a New Weighted Hilbert Inequality. J Inequal Appl 2008, 637397 (2008). https://doi.org/10.1155/2008/637397
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/637397

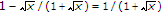 , hence we can write
, hence we can write 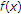 in the form of:
in the form of: 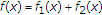 , where
, where 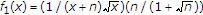 and
and 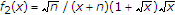 . It is obvious that the functions
. It is obvious that the functions 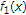 and
and 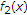 are monotonously decreasing in
are monotonously decreasing in 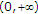 . So,
. So, 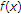 is also monotonously decreasing in
is also monotonously decreasing in 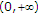 . In the next place, notice that
. In the next place, notice that  , therefore we can write
, therefore we can write 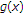 in the form of:
in the form of: 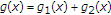 , where
, where 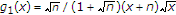 and
and 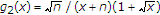 . It is clear that the functions
. It is clear that the functions 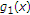 and
and 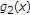 are monotonously decreasing in
are monotonously decreasing in  . So,
. So, 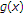 is also monotonously decreasing in
is also monotonously decreasing in  .
.