- Research Article
- Open access
- Published:
Some Characteristic Quantities Associated with Homogeneous -Type and
-Type and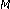 -Type Functions
-Type Functions
Journal of Inequalities and Applications volume 2007, Article number: 084146 (2007)
Abstract
Several characteristic quantities associated with homogeneous -type and
-type and -type functions are introduced and studied in this paper. Further, the concepts of
-type functions are introduced and studied in this paper. Further, the concepts of -property and
-property and -property for a couple of functions are introduced and some quantities for a pair of homogeneous functions having
-property for a couple of functions are introduced and some quantities for a pair of homogeneous functions having -property and
-property and -property are obtained, respectively. As an application, a bound for the solution of the homogeneous complementarity problem with a
-property are obtained, respectively. As an application, a bound for the solution of the homogeneous complementarity problem with a -type function is derived.
-type function is derived.
References
Fiedler M, Pták V: On matrices with non-positive off-diagonal elements and positive principal minors. Czechoslovak Mathematical Journal 1962, 12(87): 382–400.
Cottle RW, Pang J-S, Stone RE: The Linear Complementarity Problem, Computer Science and Scientific Computing. Academic Press, Boston, Mass, USA; 1992:xxiv+762.
Isac G: Complementarity Problems, Lecture Notes in Mathematics. Volume 1528. Springer, Berlin, Germany; 1992:vi+297.
Isac G: Topological Methods in Complementarity Theory, Nonconvex Optimization and Its Applications. Volume 41. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xiv+683.
Mathias R, Pang J-S: Error bounds for the linear complementarity problem with a
 -matrix. Linear Algebra and Its Applications 1990, 132: 123–136. 10.1016/0024-3795(90)90058-K
-matrix. Linear Algebra and Its Applications 1990, 132: 123–136. 10.1016/0024-3795(90)90058-KXiu N, Zhang J: A characteristic quantity of
 -matrices. Applied Mathematics Letters 2002,15(1):41–46. 10.1016/S0893-9659(01)00090-8
-matrices. Applied Mathematics Letters 2002,15(1):41–46. 10.1016/S0893-9659(01)00090-8Gowda MS: On the extended linear complementarity problem. Mathematical Programming 1996,72(1):33–50. 10.1007/BF02592330
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fang, YP., Huang, NJ. & Cho, Y.J. Some Characteristic Quantities Associated with Homogeneous -Type and
-Type and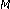 -Type Functions.
J Inequal Appl 2007, 084146 (2007). https://doi.org/10.1155/2007/84146
-Type Functions.
J Inequal Appl 2007, 084146 (2007). https://doi.org/10.1155/2007/84146
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/84146
 -matrix. Linear Algebra and Its Applications 1990, 132: 123–136. 10.1016/0024-3795(90)90058-K
-matrix. Linear Algebra and Its Applications 1990, 132: 123–136. 10.1016/0024-3795(90)90058-K -matrices. Applied Mathematics Letters 2002,15(1):41–46. 10.1016/S0893-9659(01)00090-8
-matrices. Applied Mathematics Letters 2002,15(1):41–46. 10.1016/S0893-9659(01)00090-8